一道經典試題的研究與拓展

● (溫州中學 浙江溫州 325014)

一道經典試題的研究與拓展

●馬玉斌(溫州中學 浙江溫州 325014)

閱讀張景中先生的“走進教育數學叢書”之一《繞來繞去的向量法》，書中第75頁例5.21引起了筆者的興趣.

圖1

圖2

題目如圖1，在△ABC內任取一點O，用SA,SB,SC分別表示△BOC,△COA,△AOB的面積，則

本文對這一問題進行探討，并進一步對問題加以拓展.

1 證法探究

原題即證

e1sinα+e2sinβ+e3sinγ=0.

設x=e1sinα+e2sinβ+e3sinγ,因為

x·e1=(e1sinα+e2sinβ+e3sinγ)·e1=sinα+sinβcosγ+cosβsinγ=sinα+sin(2π-α)=0,

同理

x·e2=0，

所以

x=e1sinα+e2sinβ+e3sinγ=0.

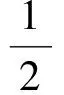
同理可得

S△C′O′A′=S△A′O′B′=SASBSC，

圖3

圖4

因此

S△A′O′B′=S△C′O′A′=SB′O′C′，

證法3如圖3，過點O作OE//BC,OD//AC.設點O到邊BC,AC,AB上的高依次為ha,hb,hc，則

證法4如圖4,延長BO交AC于點D,原題即證

懷遠石榴雖然品質良好，但是缺乏宣傳，知名度十分有限。懷遠縣的石榴很少利用新媒體的宣傳方式，只是依靠品質與口碑擴大銷路。當今社會，信息繁多，如何吸引消費者的關注成為了產品銷售的重要因素之一。“酒香不怕巷子深”的時代早已不復存在，缺乏宣傳的產品很容易導致無人問津。而懷遠的石榴卻恰恰忽視了宣傳這個重要因素。雖然懷遠的石榴拿到了國家的農產品獎項，但是由于缺乏宣傳，懷遠石榴的知名度僅限于安徽省北部的地區(qū)即周邊省。這樣會使得即使懷遠石榴及其相關產品生產出來，也只會積壓在倉庫內，造成資源浪費。因此，知名度小是該地區(qū)石榴產業(yè)化的重大阻礙。

故

證法5設∠BOC=α，∠COA=β，∠AOB=γ.因為

圖5

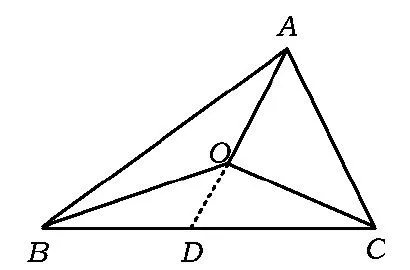
圖6

同理可得

證法6已知有結論1和結論2：

圖7

故

即

從而

2 問題拓展

圖8

類似地必有：

從而

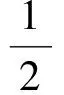
拓展2設點O是△ABC所在平面上的一點，則

利用原題的結論及五心的性質，可以得到證明(略).

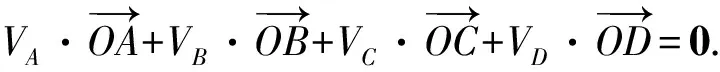
類似于平面向量的結論，建立空間直角坐標系，同樣可以證明，限于篇幅略去.

[1]張景中，彭翕成.走進教育數學：繞來繞去的向量法[M].北京：科學出版社，2010.

[2]江建國，趙曙.只有“放”得充分才能“收”得有效——“平面向量的幾何意義及應用”復習課簡錄及思考[J].中學數學，2011(5)：21-22.

[3]鮑利人，李太新 .三角形“五心”向量形式又一充要條件及其證法[J].數學通訊,2004(8):16-17.