柱狀節理巖體原位變形試驗力學淺析與模擬

狄圣杰，徐衛亞，王 偉，吳關葉

（1.河海大學 巖土力學與堤壩工程教育部重點實驗室，南京 210098；2. 河海大學 巖土工程科學研究所，南京 210098；3.中水顧問集團華東勘測設計研究院，杭州 310014）

1 引 言

白鶴灘水電站是我國擬建的一座千萬千瓦級的大型水電工程，也是西電東送的骨干電源點，壩址區玄武巖柱狀節理較為發育，如圖1所示，并且越來越多的水利工程（如金沙江下游的溪洛渡、烏東德等水電站）均揭露出大量柱狀節理玄武巖體，從傳統工程地質質量分類來看，屬于完整性較差的巖體，其變形性能是否滿足高拱壩壩基嚴格的變形要求是工程界廣泛關注的問題。

由于在柱狀節理玄武巖地區進行工程建設的需要，柱狀節理玄武巖工程特性的研究也得到了開展。石安池等[1]在研究白鶴灘柱狀節理玄武巖特點的基礎上，對影響柱狀節理玄武巖巖體變形特性的因素和變形性能各向異性的原因作了工程介紹和解釋說明；徐衛亞[2－3]、孟國濤[4]、鄭文棠等[5]對白鶴灘柱狀節理巖體本構關系、參數取值、屈服準則及數值方法等各方面進行了詳細的研究，并在壩基工程進行了應用[6]；Sharma等[7]建議采用柔性承壓板試驗來反映節理巖體的變形模量；Unal[8]的研究也表明，在現場測試巖體參數時，必須考慮松動圈對測試結果的影響，強調了中心孔變形試驗的重要性；張宜虎[9]、楊春和等[10]對中心孔變形試驗資料和循環加卸載巖體變形特性進行了試驗解釋及應用研究；Palmstrom[11]在分析洞室的承壓板試驗曲線時進行了論述，同時認為這種初始加載階段曲線不應當計入整體變形模量的計算中，且對節理巖體的原位測試機變形模量的估算做了較多的理論研究工作；Brady等[12]對大尺寸節理玄武巖體的加卸載規律性進行了詳細分析，得出典型性的3個階段力學行為。本文利用理論分析和數值模擬針對原位變形試驗資料對節理剛度取值、單節理巖體加、卸載變形規律、多組貫通節理各向異性特征及柱狀節理隨機模型模擬等問題進行探討。

圖1 白鶴灘壩址區可視化模型與柱狀節理巖體Fig.1 Baihetan visual model dam site and columnar jointed rock

2 基于原位試驗資料的節理剛度反分析

結構面參數通常應用室內試驗或經驗方法進行估算，除此之外還可運用現場中心孔試驗法來進行估算[13]。節理剛度可通過節理閉合試驗及剪切試驗確定，但試樣取樣、搬運、制備要求嚴格、繁瑣，同時不可避免地存在尺寸效應問題和試件代表性問題。而利用現場中心孔試驗反分析節理參數更具說服力。

柔性中心孔原位試驗采用4枕柔性承壓板中心孔法變形法，試驗裝置如 2(a)中左圖所示，試驗時在平硐水平向、鉛直向試驗面中心部位鉆孔，孔徑φ75 mm，孔深為6 m，在5 m孔深范圍布置多點位移計。采用逐級循環加載并紀錄不同深度不同應力水平下的位移W，繪制得到多點位移計的σ-W關系曲線，如2(b)圖所示。

圖2 白鶴灘柱狀節理巖體柔性中心孔法變形試驗Fig.2 Center hole deformation test of flexible of columnar jointed rock in Baihetan

根據柱狀節理玄武巖中心孔試驗成果，9個試驗點中分為3個水平和6個豎直試驗點，位于平硐PD133和平硐PD36中。平硐PD36中的試驗點位于Ⅲ1類地層柱狀節理巖層的弱風化帶中，為3個水平試驗點EC36Z-101、EC36Z-102、EC36Z-103和3個豎直試驗點 EC36Z-201、EC36Z-202、EC36Z-203，其中EC36Z-101試驗點報廢。平硐PD133中的試驗點位于為的微風化帶中，為3個豎直試驗點EC133Z-201、EC133Z-202、EC133Z-203。試驗點成果如表1所示。

表1 柔性中心孔法變形試驗的試驗點資料Table 1 Center hole deformation test of flexible test point data

分析白鶴灘柱狀節理玄武巖的巖體強度變化規律可知：同一巖層內，弱風化帶的變形模量低于微風化帶的變形模量；同一風化層的相同深度范圍內，受傾斜柱狀節理面影響，豎直方向的變形模量低于水平方向的變形模量；同一風化層的不同深度范圍內，受卸荷影響，淺部巖體的變形模量低于深部巖體的變形模量。符合以上規律的柔性中心孔試驗點為：EC36Z-103、EC36Z-201、EC36Z-202、EC36Z-203、EC133Z-201、EC133Z-202，考慮到松弛圈的厚度約為70～120 cm，概化原位試驗地層為兩層：試驗點以孔深86 cm以內為松弛柱狀節理巖體，孔深86 cm以下為未松弛柱狀節理巖體。

由以上試驗點資料可以估算不同風化程度、松弛程度柱狀節理面剛度系數的有效個數為：

（1）弱風化層松弛巖體，可估計節理面參數，水平方向1組，豎直方向3組；

（2）弱風化層未松弛巖體，可估計節理面參數，豎直方向1組；

（3）微風化層松弛巖體，可估計節理面參數，豎直方向2組；

（4）微風化層可估計節理面參數，豎直方向 2組。

由于結構面的變形是非線性且不可恢復的，而巖石的彈性變形是可恢復的，因此，利用某級循環荷載下的應力差和相應的變形差可估算結構面的剛度[3]。如圖2所示，S1為柱狀節理面的平均間距，可以用柱體直徑代替；S2為橫節理的平均間距，可以用柱體乘以縱橫比得出。利用中心孔試驗成果，對于水平孔和鉛直孔分別有如下關系式：

式中：Δhi為不同的深度測點距離差；、′為不同深度段的平均應力；Δ Wi+1-ΔW 為每段巖體整體變形量減去巖石受壓而產生的壓縮量，即結構面的變形量；、根據Boussinesq彈性理論近似求得，承壓面積中心以下深為zi處的鉛直應力為

式中：q為受荷表面的均布壓力；a為中心孔試驗板半徑；zi為深度。

假定1、2組結構面有相同的剛度，通過每兩級加載間各測點的應力差和位移差，根據式（1）～（4）可估算出單一節理面的剛度系數，反分析成果見表2。

表2 柔性中心孔試驗點原位試驗資料反分析成果Table 2 Flexible center hole test points, the back analysis of in situ test results

3 節理巖體加載、卸載力學變形特性

初始加載階段，表現為對應斜率較低，但斜率增長速率很快的上凹曲線。對于這種上凹曲線的物理機制，試驗點總是會受到開挖爆破的擾動而產生卸荷以致松動張開，因此，在這個階段節理均表現為壓密閉合，不能代表原巖無擾動下的狀態。巖體壓密階段斜率為斜率Ⅰ，之后進入加載階段，斜率為斜率Ⅱ，為較平直的一條準直線，表現了巖塊的壓縮變形及節理的壓縮和剪切變形共同作用的結果；初始卸載階段表現為斜率為斜率Ⅲ的曲線，斜率相對較高，后繼卸載階段對應較緩的曲線，斜率為斜率Ⅳ[4,14]。

取含一條封閉節理的巖體進行力學分析，節理閉合，建立概念模型如圖 3(a)所示，巖體尺寸長為B、寬為 W、高為 H，將巖塊視為各向同性的彈性體，巖塊的壓剪剛度分別是km、kn，彈性模量為E，巖體等效剛度為k，節理面法向與加載方向成傾角β，節理的法向剛度和切向剛度分別為Kjn和Kjs，摩擦角為φ，封閉節理長l，沿其跡線總長為L，模型上施加作用力F。單節理巖體加卸載曲線如圖3(b)所示，PD36典型承壓板試驗曲線如圖3(c)所示，由于節理的相互作用，初始卸載曲線不為直線回彈，表現為斜率漸小的曲線回彈。

假設巖石是理想彈性體，節理剛度值不隨應力而改變，節理巖體中各點的應力狀態與完整巖石應力狀態相同，這對于較致密、剛度較大的玄武巖體是合適的。先研究貫通節理巖體的變形，沿加載方向巖體的軸向變形量為兩部分產生的變形之和u=urn+ujs+ujn，剛度滿足以下關系式：

式中：urn、ujs、ujn分別為巖塊、節理切向和節理法向產生的沿加載方向的變形；kjn和kjs為由節理法向剛度Kjn和切向剛度Kjs對沿加載方向剛度的貢獻，kj為作用力與變形的關系，單位為N/m，Kj為應力與變形的關系，單位為N/m3。節理和巖塊產生的沿加載方向的變形為

圖3 單節理巖體概念模型及典型荷載變形曲線示意圖Fig.3 Conceptual model of a single rock mass and the typical load deformation curve diagram

對應的剛度分別為

對于未貫通節理，不考慮巖橋與節理接觸部位的尖端應力集中等因素，對上述貫通節理的式子進行修正，巖橋與節理的聯合剛度采用加權平均等效考慮，節理的貫通率定義為0 ＜η=l/ L ＜1，如圖4所示，則：

式中：Krn、Krs、Kjn、Kjs分別為巖石和節理的壓剪剛度，分別由其壓剪試驗確定；和為考慮節理與巖橋單元的等效剛度。對于未貫通節理單元，需用式（12）和（13）替代式（6）～（11）中的Kjn和Kjs。

故加載階段滿足以下關系：

式中：T為節理端部產生的拉力；N為力學等效連續節理上法向力；f為沿節理面的摩擦阻力；us′為端部產生的沿節理面的阻變形；u′為巖體變形總量。

圖4 非貫通節理介質Fig.4 Non-jointed media

將式（16）代入式（17）得加載階段曲線的斜率為

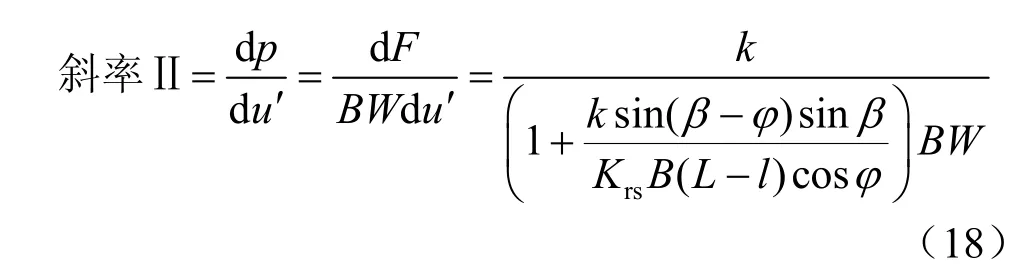
當豎向荷載按一定速率被移除時，則節理巖體將產生一個反方向的回彈變形，節理面上的摩擦阻力作用相反，當摩擦阻力足夠大，能阻止節理面向上滑移時，反彈值只有巖體的變形值而無節理的滑移值，則 斜率I II=k/ BW 。同理卸載滿足：

如果取模型為單位長度尺寸的正方體，則3者斜率蛻化為

柱狀節理傾角一般在 70°以上，則斜率Ⅳ＜斜率III ，斜率II＜斜率III 。一個完整的加載循環包括加載階段巖體變形，節理面存在非線性力學行為；初始卸載變形階段只存在巖體變形回彈；后繼卸載階段巖體變形回彈節理面存在非線性力學行為，如圖3(b)所示，表明概念模型是能夠反映承壓板試驗成果的。

對于多節理巖體的循環加載試驗，表現為初始卸載階段為斜率遞減的卸載曲線，各級卸載曲線不沿加載曲線路徑。在初始卸載階段才能抑制節理的非彈性變形，可代表節理巖體真實的彈性力學行為，在計算節理巖體等效彈性模量時，應采用承壓板原位試驗中的初始卸載階段曲線。

一般荷載低于巖石的屈服強度，認為其滯后完全是由于節理的非線性行為導致，如圖 3(c)所示，原位典型上凹型試驗曲線具有層理裂隙等結構面的非均質巖體特征，反映了隨著壓應力的增加結構面逐漸被壓密，加載模量隨之增大的趨勢，另一方面巖體各條卸載曲線在卸載到應力水平較低時，曲線斜率明顯減小，可以說明卸載后裂隙發生了松弛，發生張開和擴展。

4 基于變形解析式的巖體各向異性特征

對于一定尺度下的巖體，在某應力作用下，由式（6）～（8）可得多組節理情況下加載方向產生的總變形滿足以下關系式：

含一條L長度節理的巖體變形量為

對于隨機分布貫通節理的巖體變形量普遍的形式為

式中：m為節理的條數，對于有厚度節理單元，用節理單元的厚度代表其間距；βi為第i條節理法向與加載方向的夾角；H為加載方向的巖體尺寸；W為垂直加載方向巖體尺寸； Licosβi/W反映對加載方向的等效變形量的貢獻，即有效長度比，不同節理貫長度的影響其實是由于節理面接觸面積的影響。求得巖體平行于加載方向的等效變形模量為

由于引入了加載方向與節理法向的夾角，針對不同的方向加載，可以反映變形模量的變化規律和巖體的各向異性特征。當節理為兩組等密正交節理時，如圖5所示，正方形巖塊尺寸10 m，節理為正交，間距為0.5 m，巖塊彈性模量為50 GPa，節理法向剛度為50 GPa/m，k為切向剛度與法向剛度比值，根據式（26）～（27）得到不同節理傾角時的等效彈性模量極坐標。

圖6(a)為兩組正交節理法向剛度相等時，巖體彈性模量隨節理切向剛度與法向剛度比值k的變化曲線。圖6(b)為第1組節理法向剛度為其正交的第2組節理2倍時的曲線，圖中 k=Ks/Kn，曲線代表彈性模量隨節理切向剛度與法向剛度比值從0.1變化至 5.0時對應的曲線。各向異性曲線特征與 Ki-Bok[15]揭示的規律一致。

隨著 Ks/ Kn比值減小而增強，并在β接近45°時達到極值。當兩組節理剛度特性不同時，即水平向節理剛度為豎直向節理的2倍時，呈扁平化特征；由于兩組節理間距相同，節理剛度相同，則表現為各向同性特征，對應為球形。且 Ks/Kn=1時，雖然兩組節理間距相同，但節理剛度不同，仍表現為各向異性特征。由于式（26）～（27）是通式，對于任意傾角貫通節理同樣可以求解，如圖6(b)所示。對于未貫通節理巖體，根據等效剛度來確定，將式（12）～（13）中等效剛度代入通式（26）～（27）中即可得到。壩址區柱狀節理玄武巖體的柱體與其主軸夾角約為15°，柱元直徑S1約為0.2 m，柱體長度S3約為1 m，巖塊彈性模量取為65.1 GPa，節理法向剛度與切向剛度分別取 284.48 GPa/m和99.31 GPa/m。概化模型如圖7所示，通過式（27）計算得到主軸坐標系下彈性模量E3和E1分別為53 GPa和30.4 GPa，主軸偏轉15°后xy坐標系下Ey與Ex分別為31.6 GPa和27.1 GPa。

圖5 正交節理巖體與隨機節理巖體Fig.5 Orthogonal jointed rock with random jointed rock

圖6 二維正交節理巖體各向異性特征曲線Fig.6 Two-dimensional orthogonal anisotropy curves of jointed rock

圖7 柱狀節理巖體柱體偏轉示意圖Fig.7 Deflection diagram of columnar jointed rock column

5 承壓板變形試驗數值模擬

Hart等[16]指出，BWIP規則六邊形柱狀節理巖體原位變形試驗揭示出的滯后效應、應變分布的不均勻性及剛度的圍壓效應都可以歸結為節理網絡的非線性行為造成。Hart等采用數值試驗分析了規則六邊形柱狀節理巖體原位變形試驗中揭示的滯后行為，認為柱狀節理的轉動和滑移是柱狀節理巖體非線性行為的根本原因，如圖8所示。

圖8 BWIP規則六邊形柱狀節理數值模擬結果[16]Fig.8 Numerical simulation results of BWIP rules hexagonal columnar joints[16]

此處基于不規則柱元形狀的離散元數值構建方法，采用Voronoi構建語法，在6 m×3 m的區域內，采用平均邊長為0.2 m，迭代次數小于100來控制柱面形狀以四邊形和五邊形為主，生成與現場勘查較一致的柱狀節理數值模型，如圖9所示。

承壓板寬度為2 m，參數選取如表3所示，巖體節理剛度初始加載階段采用松弛節理剛度Kn0和Ks0，為初始加載壓密階段的參數，壓密后采用未松弛節理剛度Kn和Ks。分4級加、卸載，每級以2 MPa為單位加、卸載，反映的是白鶴灘柱狀節理巖體垂直于柱體方向應力-變形關系。建立多組隨機柱狀節理模型，得到多組加卸載曲線，可得到多組數據的平均變形模量與彈性模量值。

豎向變形與應力云圖如圖10所示，模擬的加、卸載曲線如圖11所示。

圖9 原位橫截面素描圖與生成的Voronoi模型Fig.9 Sketches of the cross-section of in-situ generation diagram and Voronoi model

表3 不規則柱狀節理參數Table 3 Parameters of irregular columnar joints

圖10 豎向變形與應力云圖Fig.10 Vertical deformations and stress nephograms

圖11 原位加卸載模擬曲線Fig.11 Simulation curves of in-situ loading and unloading

卸載階段結束后，節理巖體存在不可恢復的永久變形，與原位試驗初始卸載曲線吻合較好，單節理力學概念模型的初始卸載曲線是直線，復雜節理情況下為多折線型曲線，斜率逐漸減小，表明模擬的柱狀節理加、卸載力學行為及滯后特性效果較好。豎向應力從表面向深部隨機延伸，這有別于各向同性材料,顯現出各向異性特性。在應力較大時可能形成節理滑移的應力臨界條件，可理解為塊體在應力作用下局部排列方式的改變，由平動和偏轉導致。根據資料統計[4]，Ⅲ1類地層微風化帶左岸柱狀節理巖體垂直于柱體方向的變形模量測試值為 18.86～36.25 GPa，彈性模量測試值為28.83～41.20 GPa，計算變形模量為20.69 GPa，彈性模量為33.3 GPa，其值在試驗值范圍內。

6 結 論

（1）由于柱狀節理剛度值較難確定，室內試驗取樣難度也較大，利用原位測試成果反算其值是一種比較合適的方法；

（2）對節理巖體加、卸載力學性能分析，從概念模型研究入手，解釋其非線性力學行為，同時基于概念模型得到的變形公式是一通式，可以用于等效變形參數的計算和節理巖體各向異性的分析；

（3）應用由現場測試結果反算的節理剛度值和離散元方法進行了柱狀節理的模擬計算，規律性與現場試驗結果一致，所得彈性模量和變形模量均在實測值范圍內，文中所采用方法可為涉及柱狀節理的工程計算及參數取值提供參考。

（4）值得指出的是，基于解析式的節理剛度反算及巖體各向異性分析，不能考慮圍壓和節理交錯影響，同時巖體在構造應力和二次應力場的作用下也會引起局部應力集中現象，并且個別柱狀節理會在加載過程中產生屈服強化，這些都會影響到巖體應變不均和滯后效應，在實際工程中需要考慮到。

[1] 石安池, 唐鳴發, 周其健. 金沙江白鶴灘水電站柱狀節理玄武巖巖體變形特性研究[J]. 巖石力學與工程學報,2008, 27(10): 2079－2086.SHI An-chi, TANG Ming-fa, ZHOU Qi-jian. Research of deformation characteristics of columnar jointed basalt at Baihetan hydropower station on Jinsha River[J]. Chinese Journal of Rock Mechanics and Engineering, 2008,27(10): 2079－2086.

[2] 徐衛亞, 鄭文棠, 寧宇, 等. 柱狀節理壩基巖體三維各向異性數值計算[J]. 巖土力學, 2010, 31(3): 949－955.XU Wei-ya, ZHENG Wen-tang, NING Yu, et al. 3D anisotropic numerical analysis of rock mass with columnar joints for dam foundation[J]. Rock and Soil Mechanics, 2010, 31(3): 949－955.

[3] 徐衛亞, 狄圣杰, 鄭文棠, 等. 白鶴灘水電站上壩線左拱座楔形體安全性能分析[J]. 巖石力學與工程學報,2011, 30(5): 910－916.XU Wei-ya, DI Sheng-jie, ZHENG Wen-tang, et al.Safety performance analysis of rock wedges under left skewback of upstream dam line in Baihetan Hydropower Station[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(5): 910－916.

[4] 孟國濤. 柱狀節理巖體各向異性力學分析及其工程應用[D]. 南京: 河海大學, 2007.

[5] 鄭文棠. 不規則柱狀節理巖石力學及在高邊坡壩基巖石工程中的應用[D]. 南京: 河海大學, 2008.

[6] DI Sheng-jie, XU Wei-ya, NING Yu, et al.Macro-mechanical properties of columnar jointed basaltic rock masses[J]. Journal of Central South University of Technology, 2011, 18(6): 2143-2149.

[7] SHARMA V M, SINGH R B, CHAUDHARY R K.Comparison of different techniques and interpretation of the deformation modulus of rock mass[J]. Proc. Indian Geotechnical Conference IGC. Visakhapatnam, 1989,I: 439.

[8] UNAL E. Determination of in situ deformation modulus:New approaches for plate-loading tests[J]. International Journal of Rock Mechanics and Mining Sciences, 1997,34(6): 897－915.

[9] 張宜虎, 石安池, 周火明, 等. 中心孔變形試驗資料的解釋與應用[J]. 巖石力學與工程學報, 2008, 27(3): 489－595.ZHANG Yi-hu, SHI An-chi, ZHOU Huo-ming, et al.Explanation and application of data obtained in deformation test of central hole[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(3): 489－595.

[10] 楊春和, 馬洪嶺, 劉建鋒, 等. 循環加、卸載下鹽巖變形特性試驗研究[J]. 巖土力學, 2009, 30(12): 3562－3568.YANG Chun-he, MA Hong-ling, LIU Jian-feng, et al.Study of deformation of rock salt under cycling loading and unloading[J]. Rock and Soil Mechanics, 2009,30(12): 3562－3568.

[11] PALMSTROM A, SINGH R. The deformation modulus of rock masses—comparisons between in situ tests and indirect estimates[J]. Tunnelling and Underground Space Technology, 2001, 16(2):115－131.

[12] BRADY B H G., CRAMER M L, HART R D.Preliminary analysis of a loading test on a large basalt block[J]. Int. J. Rock Mech. Min. Sci. & Geomech.Abstr., 22: 345－348.

[13] 劉佑榮, 唐輝明. 巖體力學[M]. 武漢: 中國地質大學出版社, 1999.

[14] Itasca Consulting Group Inc. Verification problems and example applications, version 4.0[M]. Minneapolis: [s. n.],2003.

[15] KI-BOK M. Fractured rock masses as equivalent continua——A numerical study[D]. Stockholm: KTH University,2004.

[16] HART R D, CUNDALL P A, CRAMER M L. Analysis of a loading test on a large basalt block[J]. Research &Engineering Applications in Rock Masses, Proceedings of the 26th US Symposium on Rock Mechanics, 1985,2: 759－768.