深基坑施工變形預測VAR建模與應用分析

代春泉，王 磊

（1.山東科技大學 土木建筑學院, 山東 青島 266590；2.山東科技大學 山東省土木工程防災減災重點實驗室，山東 青島 266590）

1 引 言

隨著經濟社會的發展，城市人口的增加，城市規模在橫向延伸的同時也在向縱向拓展，體現為城市建筑高度的增加和密度的增大，深基坑施工問題越來越突出，尤其在大中城市中深基坑施工面臨問題更多，呈現出深大、近緊的特點[1－3]。施工過程中的各個環節都有可能引發惡性的工程事故，嚴重影響周邊居民生活與社會生產，不僅帶來巨大的經濟損失，還嚴重影響正常的社會文化生活。基坑施工穩定性控制問題一直是國內外專家研究的熱點，歷經幾十年的研究與發展，取得了大量的、有價值的研究成果。

在基坑施工變形力學分析方面，Thomas[4]通過對大量實測數據和模型試驗結果的比較，得出墻體位移與地表沉降的變化規律；OU Changyu等[5]研究了擋墻最大位移位置、大小，擋墻最大水平位移與最大地表沉降的關系，最大地表沉降的位置，并給出了開挖顯著影響區范圍。Attwell[6]探討了地下工程或基坑開挖引起的地面沉降，以及對地面建（構）筑物和地下管線的影響。Nakai[7]采用MITE3模型模擬分析了Boston深基坑開挖變形分布，以及對周邊建筑物的影響，通過對基坑開挖側向變形的數值模擬分析總結，認為最大側向變形是開挖深度和支撐間距的函數。侯學淵等[8]根據墻體水平位移和地表沉陷相關原理，并借用三角形沉降公式采用有限元方法，分析了地面沉降和墻體水平位移的分布規律。劉國彬等[9]結合上海軌道交通地鐵深基坑變形監測，對不同坑底暴露時間所對應的支護墻體變形分布進行了綜合分析。龔曉南等[10]采用三維有限元理論，分析了深基坑施工過程支護結構的內力分布規律，以及土層應力分布的空間規律和變形特 征，并對基坑開挖力學問題的尺寸效應進行了探討性研究。

上述專家從不同角度采用不同方法研究了基坑施工變形力學問題，這些成果對揭示基坑施工變形力學機理，定性分析基坑施工變形分布規律方面具有重要意義。但是，隨著基坑施工規模增大，深度增加，傳統力學問題并不能定量解決深基坑變形分析與穩定性控制難題，于是一部分專家尋求新的途徑——變形預測分析基坑施工變形問題。

所謂變形預測是采用數理統計方法，如灰色理論、神經網絡方法、隨機理論等建立預測模型，以基坑施工前期部分監測數據為樣本預測其后一定時間內的變形發展。這一方面的主要研究成果有，繆新穎等[11]對傳統的 BP神經網絡變形預測進行改進，提出了具有較快收斂速度和較強泛化能力的LM-BP變形預測模型。廖展宇等[12]采用非等間距時序灰色預測模型分析了基坑施工變形的時間變化特征，經過工程實例分析，該模型精度高，滿足中期預測分析要求。賈備等[13]則將灰色系統理論與BP神經網絡模型進行有機聯合，建立了灰色BP神經網絡組合模型的預測方法。李水兵等[14]采用雙曲正切函數作為輸入輸出的傳遞函數，建立了深基坑變形預測的BP神經網絡預測模型，并采用附加動量法對模型進行自適應修正。劉開云等[15]根據現場監測分析了邊坡位移序列的非線性特點，采用模糊神經推理系統和遺傳算法，建立邊坡變形預測的進化-自適應神經網絡模糊推理模型，并進行了實例驗證分析，分析結果表明該模型比傳統的GA-SVR模型、GA-BP模型精度高。沙成滿等[16]針對現場監測數據與實際變形值的偏差，以小波去噪理論，建立改進的灰色自適應變形預測模型進行深基坑施工變形預測分析，并進行了初值修正和殘差分析，經過工程實例驗證，該模型具有較高的精度。

從上述研究成果來看，變形預測已成為基坑施工既有支護效果評價，施工安全預警的重要方法。但是根據實際應用情況，基坑施工變形預測還存在精度低，預測時效性差的問題。

向量自回歸模型（VAR）及其衍生模型因其應用方便、預測精度高等優點在金融分析、經濟預測等領域得到廣泛應用，本文嘗試采用 VAR模型預測深基坑施工變形。

2 深基坑變形預測與VAR模型

2.1 變形預測基本原理

目前我國深基坑施工設計還是以經驗設計為主，施工過程中以監測信息反饋為指導修正既有支護方案，并分析施工安全性。傳統方法認為，監測值趨于穩定變意味著支護結構的安全性[17]。這種模式監測信息反饋具有滯后性，不能及時調整支護參數，支護調整越滯后，支護成本越高，而且容易引起變形失控，引發工程事故。因此根據既有的監測數據建立數學預測模型及時調整支護參數，對優化施工方案、調整支護參數、保障施工安全具有重要意義。變形預測以既有支護條件下變形監測數據為小樣本，通過一定的數學模型進行預測分析，檢查模型精度并調整進而服務于基坑施工，具體流程如圖1所示。

圖1 基坑施工變形預測流程Fig.1 Prediction flow of construction deformation of foundation pit

2.2 基坑變形實測分析

向量自回歸模型VAR于20世紀90年代在經濟、金融等領域得到廣泛應用[18－19]，到本世紀初開始在工程領域應用，如風速預測、浪高預測、水流預測、降水預測等[20－21]。

基坑施工變形監測數據一般以天(d)為單位繪制變形曲線，如圖2所示。

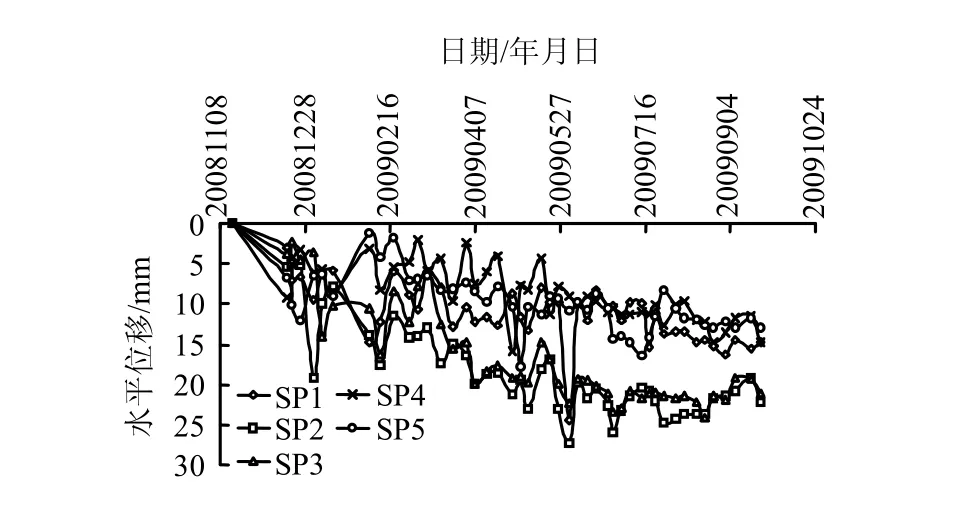
圖2 基坑施工變形實測曲線Fig.2 Measured curve of construction deformation of foundation pit

從圖2的基坑施工變形實測曲線來看，變形呈現波動規律，但從長期變形發展來看又有一定的規律可循，而這種短期非平穩、長期有規律的變形特點適合采用VAR模型進行建模預測分析。

2.3 基坑變形預測VAR模型

將基坑變形監測數據以時間序列記為U(t)，t =1, 2, …, n的單位時間間隔，根據不同分析的需要可取△t為1、2、10、30 d等。同一天內不同監測時間的變形-時間序列寫為向量的形式，即

式中：下標d表示測試日期天數；下標k為向量維數，表示每天監測的次數。

對于式（1）中向量變形-時間序列Ud，可以建立n階的VAR模型：

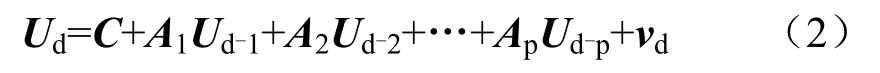
式中：Ai為模型參數矩陣，可根據已監測數據求得；vn是均值為0的分布相同的噪聲向量；C為常數向量。

對式（2）作均值處理，可得

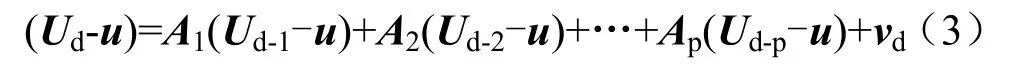
式中：u為建模樣本數據均值。

為簡化分析，定義以下向量和矩陣：

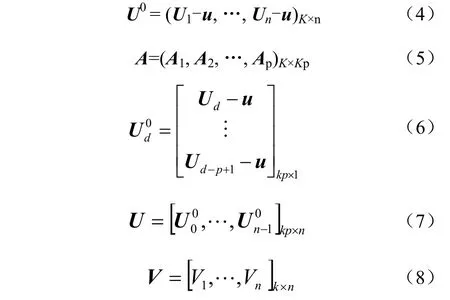
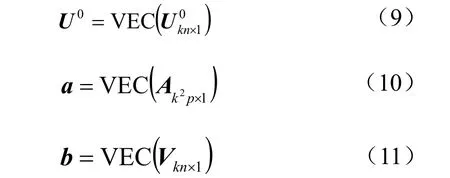
因此可將式（3）改寫為

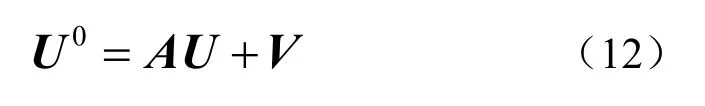
進一步可將式（12）寫為

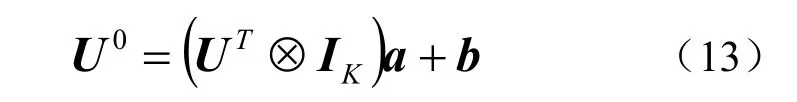
式中：IK為K階單位矩陣。

取對數似然函數：

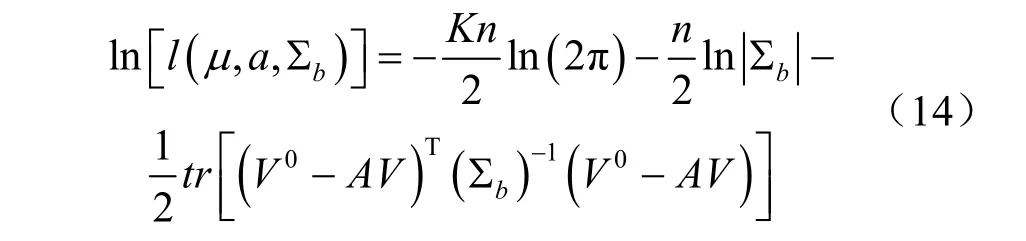
式中：∑b為V的協方差矩陣。

分別對式(14)似然函數求偏導數，便可得到參數矩陣a、b。

而對于模型階數的確定，可采用似然比統計量法或AIC法(赤木信息判據)，這里采用AIC法，即

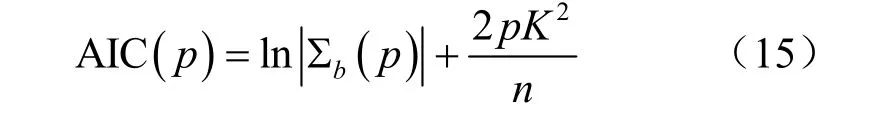
式中：∑b（p）為協方差矩陣∑b極大似然估計。

AIC法計算的具體步驟為：對p=0, 1, 2, …, n，分別計算模型參數，并計算AIC(p)，其最小值對應的p值就是VAR模型所需要的階。

2.4 VAR模型應用說明

從上述建模過程來看，計算比較復雜，實際應用過程中，由于一般監測為1 d1～2次，維數降為一維或二維，使得求解過程更加簡單。分析過程中可借助excel或matlab編程計算。

3 深基坑施工變形預測應用分析

3.1 工程概況與施工監測

濟南市省會文化藝術中心深基坑工程最大開挖深度為21.2 m，開挖深度范圍內有流砂層，且瀕臨黃河，地下水豐富。基坑施工難度大，而且工程規模大，基坑施工將跨越夏季多雨季節，對基坑安全不利。在施工過程中通過設計了合理的監測方案，密切關注施工過程中各監控值的變化，并建立預測模型預測變形發展趨勢，及時優化施工方案，保證施工安全。

3.2 預測應用分析

為檢驗文中給出的 VAR模型在深基坑施工變形預測中的應用效果，以坡頂豎向位移典型數據為樣本建立模型，進行變形預測。取圖2中典型測點SP2前期監測數據，如圖3所示。

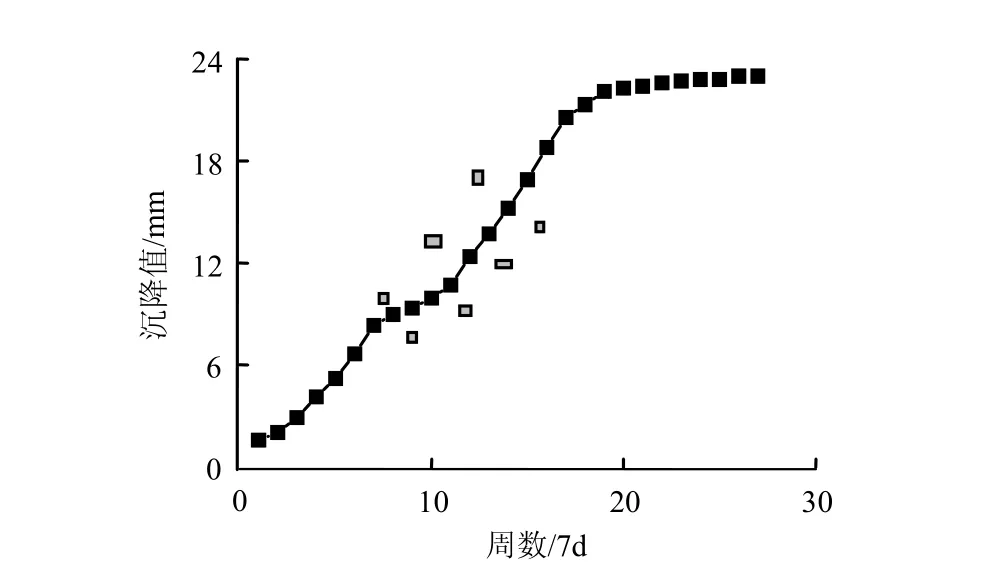
圖3 SP2監測曲線Fig.3 Measured curve of point SP2

以前35 d數據為樣本建立模型，根據AIC比較，取p=2，經過計算，預測值誤差分析見表1。

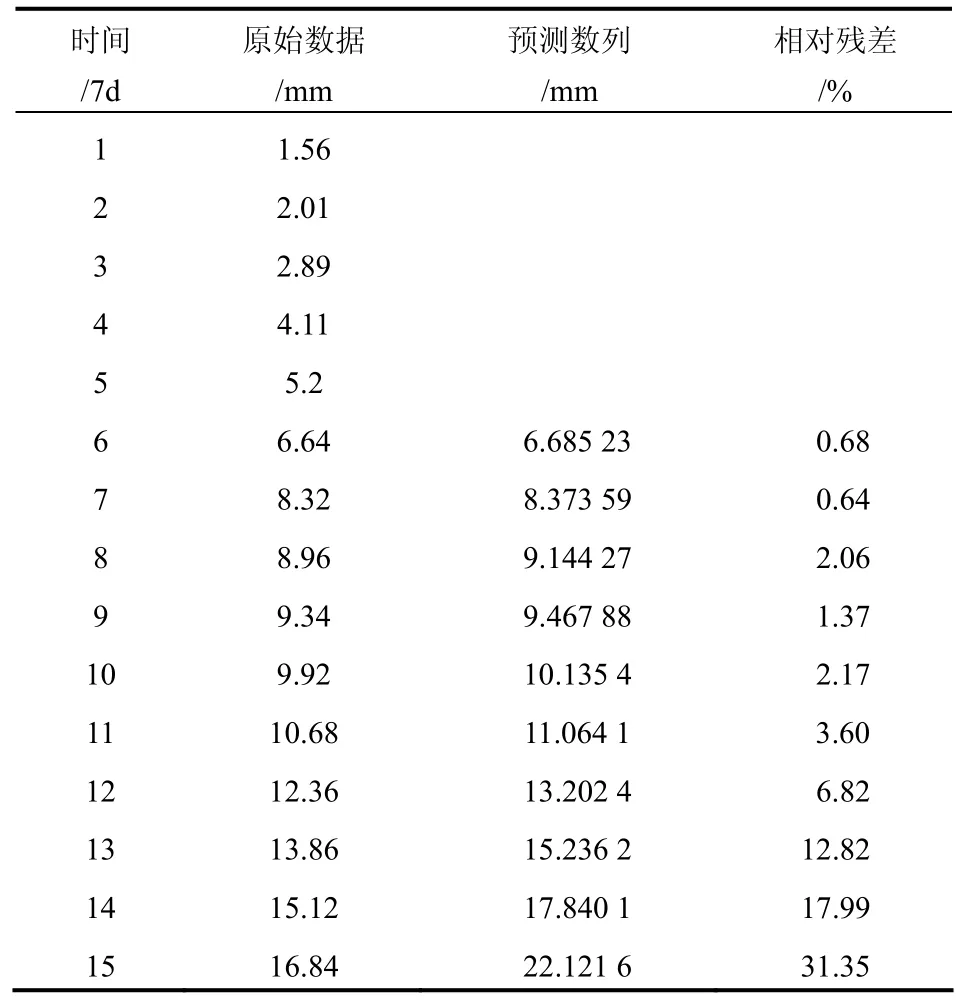
表1 VAR模型預測分析Table 1 Analysis of VAR model

根據表1中分析數據，VAR模型以前期監測數據為樣本建立模型，并且及時補充新數據，預測后期變形發展，在77 d之前誤差較小，77 d之后誤差明顯增大，98 d之后已經不可接受。

通過誤差分析，該模型進行深基坑施工變形短期預測誤差可以接受，模型精度可以滿足現場應用要求。

3.3 對比分析

為進一步分析 VAR模型的預測應用效果，選取目前常用預測模型：灰色預測模型 GM(1,1)、新陳代謝模型和神經網絡預測模型進行建模對比分析。GM(1, 1)模型是以小樣本建立白化響應式，進而求解白化微分方程，建立變形預測數列。而新陳代謝模型則是在 GM(1,1)模型的基礎上及時去掉舊信息，輸入新信息，模型精度要比 GM(1,1)高；神經網絡預測通過建立模型進行訓練獲得預測值，需要的信息量較大。以圖3中數據進行建模預測分析，并計算相應的誤差，計算結果如表2所列。

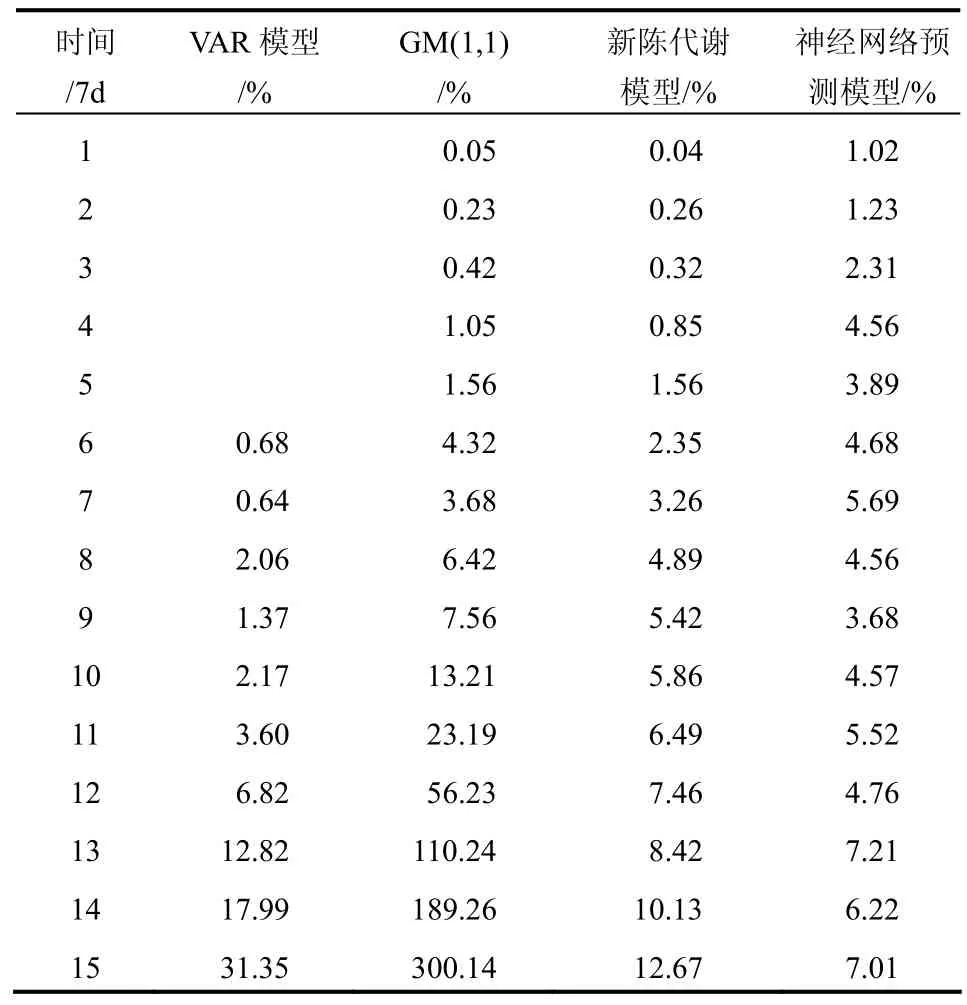
表2 4類預測模型預測精度分析Table 2 Analysis of 4 prediction models

由表2的預測結果可以看出，（1）VAR模型的預測精度要比GM(1, 1)模型、新陳代謝模型、神經網絡預測模型精度高；（2）VAR模型、GM(1, 1)模型、新陳代謝模型都出現誤差積累，后期預測精度低，只適合于短期預測，而神經網絡模型在實際應用中需要的數據樣本較多，其預測誤差相對穩定，誤差的大小與傳遞函數有關。

為分析4類預測模型的可預測時間段長與建模段長的關系，定義預測比，即

式中：ty為可接受的預測時段長；tj為建模時段長。

以相對誤差5%為標準進行分析，可得VAR模型的預測比κ為 1.0，GM(1, 1)模型的預測比κ為0.4，新陳代謝模型的預測比κ為 0.6，神經網絡預測模型由于其建模需要樣本數據多，預測比為0.56。

4 結 論

（1）深基坑施工過程中受多種因素影響，根據實際基坑施工變形監測數據，從短期分析來看，數據具有非穩定性，但從長期分析又有一定的規律，可以用向量自回歸模型進行建模分析。

（2）VAR模型在實際應用過程中，因一般監測頻率為 1次/天或 2次/天，在分析過程中使得模型降為一維或二維，計算過程簡化，而VAR模型的階一般為2或3，極少超過5。

（3）4類預測模型從預測精度上比較，依次是：VAR模型＞新陳代謝模型＞神經網絡模型＞GM(1,1)模型；而建模所需要的樣本量排序為：神經網絡預測模型＞新陳代謝模型＞VAR模型＞GM(1, 1)模型。

（4）VAR模型不適合長期變形預測，適合于短期變形發展分析，4類模型的預測比排序為：VAR模型＞新陳代謝模型＞神經網絡模型＞GM(1, 1)模型。

[1] 徐中華，王建華，王衛東.上海地區深基坑工程中地下連續墻的變形性狀[J].土木工程學報, 2008, 41(8): 81－86.XU Zhong-hua, WANG Jian-hua, WANG Wei-dong.Deformation behavior of diaphragm walls in deep excavations in Shanghai[J].China Civil Engineering Journal, 2008, 41(8): 81－86.

[2] OSMAN A S，BOLTON M D.Ground movement predictions for braced excavations in undrained clay[J].Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2006, 132(4): 465－477.

[3] 黃茂松, 宋曉宇, 秦會來.K0固結黏土基坑抗隆起穩定性上限分析[J].巖土工程學報, 2008, 30(2): 250－255.HUANG Mao-song, SONG Xiao-yu, QIN Hui-lai.Basal stability of braced excavations in K0-consolidated soft clay by upper bound method[J].Chinese Journal of Geotechnical Engineering, 2008, 30(2): 250－255.

[4] THOMAS D, ROURKE O.Ground movement caused by braced excavation[J].School of Civ.and Environmental Engrg., 1981, 107(9): 1159－1178.

[5] HSIEH P G, OU Chang-yu, HSIEH.Shape of ground surface settlement profiles caused by excavation[J].Canadian Geotechnical Journal, 1998, 35(6): 1004－1017.

[6] ATTWELL P B.Soil movement induced by tunneling and their effects or pipelines and structures[M].New York:Soil Blackie Chapman and Hall, 1986: 2046－2046.

[7] NAKAI T.Analysis of earth pressure problems considering the influence of wall friction and the wall deflection[C]//Proc., the 5th Int.Conf.on Numer.Methods in Gechanics.Japan: [s.n.]: 765－772.

[8] 侯學淵，劉國彬，黃院雄.城市基坑工程發展的幾點看法[J].施工技術，2000, 29(1): 256－261.HOU Xue-yuan, LIU Guo-bin, HUANG Yuan-xiong.Several views on the development of urban foundation work[J].Construction Technology, 2000, 29(1): 256－261.

[9] 劉國彬, 劉登攀, 劉麗雯, 等.基坑坑底施工階段圍護墻變形監測分析[J].巖石力學與工程學報, 2007, 26(增刊2): 4386－4394.LIU Guo-bin, LIU Deng-pan, LIU Li-wen, et al.Monitoring and analysis of lateral deformation of retaining wall during bottom excavation in deep pit[J].Chinese Journal of Rock Mechanics and Engineering,2007, 26(Supp.2): 4386－4394.

[10] 龔曉南.基坑工程發展中應重視的幾個問題[J].巖土工程學報, 2006, 28(增刊): 1321－1324.GONG Xiao-nan.Some major problems in the development of foundation pit engineering[J].Chinese Journal of Geotechnical Engineering, 2006, 28(Supp.):1321－1324.

[11] 繆新穎, 褚金奎, 杜小文.LM-BP神經網絡在大壩變形頂測中的應用[J].計算機工程與應用, 2011, 47(1): 220－222.MIAO Xin-ying, CHU Jin-kui, DU Xiao-wen.Application of LM-BP neural network in predicting dam deformation[J].Computer Engineering and Applications, 2011, 47(1): 220－222.

[12] 廖展宇, 李英, 晏鄂川, 等.非等間隔時序灰色模型的深基坑變形預測研究[J].合肥工業大學學報, 2009,32(10): 1522－1525.LIAO Zhan-yu, LI Ying, YAN E-chuan, et al.Study on deformation prediction of a deep foundation pit based on the unequal interval grey model[J].Journal of Hefei University of Technology, 2009, 32(10): 1522－1525.

[13] 賈備, 鄔亮.基于灰色BP神經網絡組合模型的基坑變形預測研究[J].隧道建設, 2009, 29(3): 280－284.JIA Bei, WU Liang.Research of the Prediction of foundation deformation based on gray BP neural network combined model[J].Tunnel Construction, 2009, 29(3):280－284.

[14] 李水兵, 李培現.基于 BP神經網絡的深基坑變形預測[J].測繪信息與工程, 2011, 36(5): 41－43.LI Shui-bing, LI Pei-xian.Deep Foundation pit considering excavation effect based on BP neural network model[J].Journal of Geomatics, 2011, 36(5): 41－43.

[15] 劉開云, 魏博, 劉保國.邊坡變形時序分析的進化自適應神經模糊推理模型[J].北京交通大學學報, 2012,36(1): 56－62.LIU Kai-yun, WEI Bo, LIU Bao-guo.Analysis model of slope deformation time series based on the genetic-adaptive neuron-fuzzy inference system[J].Journal of Beijing Jiaotong University, 2012, 36(1): 56－62.

[16] 沙成滿, 韓合新, 楊冬梅.基于小波去噪的改進灰色自適應變形預測[J].東北大學學報, 2011, 31(8): 1195－1197.SHA Cheng-man, HAN He-xin, YANG Dong-mei.Deformation forecast using improved self-adaptive grey model based on wavelet denoising[J].Journal of Northeastern University (Natural Science), 2011, 31(8):1195－1197.

[17] 龔曉南.土釘和復合土釘支護若干問題[J].土木工程學報, 2003, 36(10): 80－83.GONG Xiao-nan.On soil nailing and composite soil nailing[J].China Civil Engineering Journal, 2003,36(10): 80－83.

[18] 吳振信, 薛冰, 王書平.基于 VAR模型的油價波動對我國經濟影響分析[J].中國管理科學, 2011, 19(1): 21－28.WU Zhen-xin, XUE Bing, WANG Shu-ping.The impact of oil price volatility on China’s economy based on VAR model[J].Chinese Journal of Management Science,2011, 19(1): 21－28.

[19] HERRERA A M, PESAVENTO E.Oil price shocks,systematic monetary policy, and the great moderation[J].Macroeconomic Dynamics, 2009, 13: 107－137.

[20] 孫春順，王耀南，李欣然.小時風速的向量自回歸模型及應用[J].中國電機工程學報，2008, 28(14): 112－117.SUN Chun-shun, WANG Yao-nan, LI Xin-ran.A vector autoregression model of hourly wind speed and its applications in hourly wind speed forecasting[J].Proceedings of the CSEE, 2008, 28(14): 112－117.

[21] EWING B T, KRUSE J B，SCHROEDER J L, et al.Time series analysis of wind speed using VAR and the generalized impulse response technique[J].Journal of Wind Engineering and Industrial Aerodynamics, 2007,95(19): 209－219.