基于可變大小模板的改進圖像修復算法*

張 嵩，周旭亞

(杭州電子科技大學通信工程學院，杭州 310018)

圖像修復，或者圖像補全，簡單地說就是利用圖像中的已知區域信息來填充待修復區域。圖像修復的概念最早由Bertalmio等人提出［1］，他們同時給出了一種有效的基于偏微分方程(PDE)的算法，即將修復轉化為求解一個特殊的偏微分方程。類似的算法還有不少［2－4］。基于PDE模型的算法對修復局部狹長的區域比較有效，但對大面積缺失或紋理信息豐富的圖像，此類算法修復效果不夠理想。非參數紋理合成是圖像修復的另外一類重要方法，其基本思想最早可追溯至Efros與 Leung 的工作［5］。在此基礎上，Criminisi等人［6］提出了一種全新的基于模板的圖像修復算法，被公認為修復技術方面的重要突破，影響甚大。

但是Criminisi算法仍存在缺點，比如修復后圖像紋理斷層，時間復雜度較高等，對其的改進仍然是圖像修復領域的一個重要研究方向。譬如，一種徹底的解決之道是所謂的全局優化方法［7－10］，即將修復問題轉化為最小化能量泛函。不過，這類方法的復雜度太大，應用上有不小的限制。我們認為，Criminisi算法框架目前仍是修復效果與實現代價之間的最佳折衷。因此，我們在Criminisi基本算法框架之上融合了一些新的改進元素:我們采用了基于可變大小模板的塊搜索方案；并結合改進的修復像素信度(confidence)更新公式及局部搜索模式，以期獲得較好的算法綜合性能。仿真結果表明系統整體性能確實得到較大提高。

本文第二節簡單介紹Criminisi算法流程以方便后續論述，第三節具體介紹改進方法，第四節給出實驗結果比較，第五節給出總結與展望。

1 Criminisi算法

為了更好地介紹所提出的改進方案，首先簡述Criminisi算法。Criminisi算法本質上仍然屬于紋理合成方法，但卻能同時修復紋理和結構信息。假設圖像為A，待修復區域為Ω，已知(或已修復)區域記為AΩ，當前迭代次數用t表示，Criminisi算法重復以下步驟直至所有像素都被修復。

步驟1:確定當前修復邊界?Ωt，若?Ωt=?，算法退出。

步驟2:對邊界上的每一點p，以點p為中心的待修復塊記為Ψp。對每個待修復邊界點計算優先權P(p)如下:

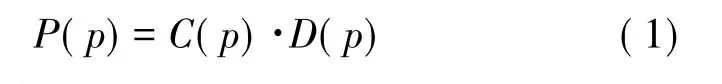
其中，信度項C(p)定義為:

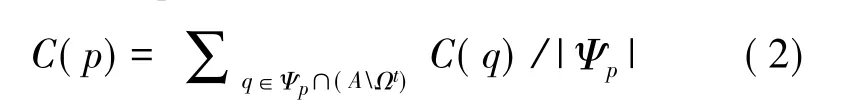
|Ψp|是塊或模板大小，也即模板像素總數。初始化時，對于待修復區域所有像素C(p)置0，其他已知像素則置為1。數據項D(p)試圖反映點p附近圖像結構強度:

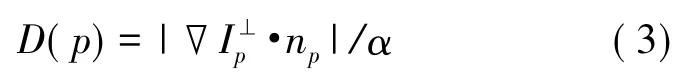
這里α是歸一化因子，np是點p處邊界?Ωt的法線單位向量，⊥表示向量90°旋轉。

步驟3:找出具有最大優先權的待修復塊Ψp*。

步驟4:在已知(或已修復)區域中搜索與Ψp*最相似的模板Ψq*:

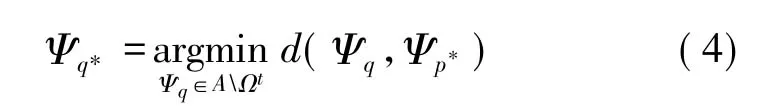
步驟5:把Ψq*中相應區域的像素值復制到Ψp*中未知區域。

步驟6:更新信度:

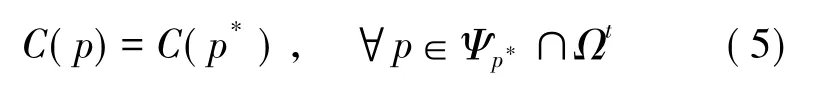
2 改進方案

Criminisi算法是一種貪婪算法，本質上是非最優(suboptimal)的，但仍不失為兼顧性能與代價的較好選擇。本文在保持算法基本框架不變的情況下加入了一些有意義的改進，以下進行詳述。

2.1 基于可變大小模板的匹配搜索

對基于紋理合成的串行修復算法來說，前面模塊的匹配搜索精度直接影響到后續塊的修復效果。這其中模板大小是一個很關鍵的參數。單從匹配精度而言，應當選擇較小的模板；而從圖像正則性及算法復雜性角度，則希望選擇較大的模板。Criminisi算法采用固定模板大小，但要設定折衷上述各點并適應不同圖像特征的模板大小參數實際上是不可能的，這就構成了Criminisi算法的一個重要不足。本文針對性地提出可變大小模板搜索框架，并對具體的搜索程序進行了細致設計。

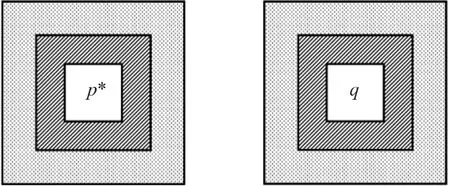
圖1 可變大小模板的匹配

如圖1所示，p*為當前修復像素，q為目標像素。我們從某一最小模板大小PSmin(比如5×5)開始進行當前模塊與目標模板之間的匹配，然后逐漸增大模板大小，從5×5到7×7，9×9 等等，直到獲得最佳匹配效果。由于相鄰大小模板或塊成嵌套關系，因此在模板增大匹配過程中，每次只需對圖1中的環狀區域進行增量計算，而勿需對共同部分重復處理。另外，因模板大小是可變的，我們采用均方誤差(MSD)而不是誤差平方和(SSD)作為相異性測度:

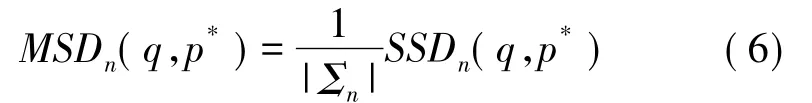
其中n表示當前模板尺寸，|Σn|是塊Ψp*中的已知像素個數。考慮到圖像正則性與計算代價，我們還在相異性測度中結合了與模板大小相關的項，如下定義:

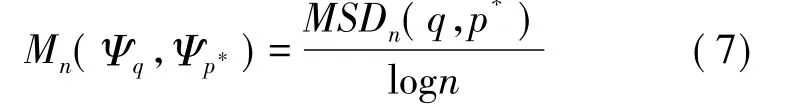
引入logn項的目的是鼓勵大模板匹配，由此形成的廣義測度有點類似于時間序列建模中的Akaike準則。兩點間的匹配過程可由以下的偽代碼緊湊描述:

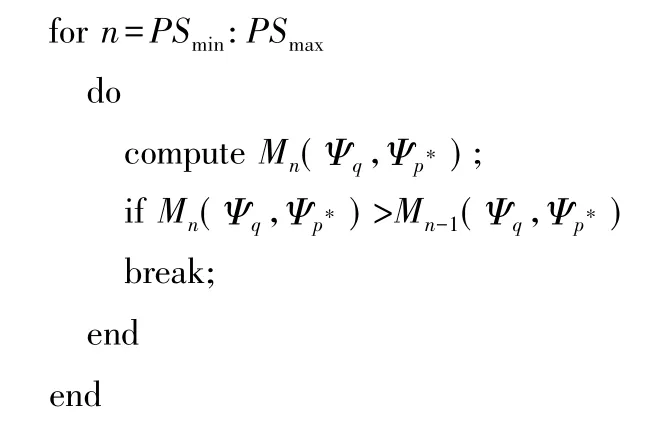
其中PSmax為設定的最大模板大小。第四行中的條件語句意味著，一旦發現模板匹配效果有下降的趨勢就終止模板擴大過程，這樣能達到精度與計算復雜度的較好平衡。匹配結束后得到的最優相異性測度記為M(Ψq，Ψp*)。

通過對已知區域進行搜索，得到最優匹配模板:

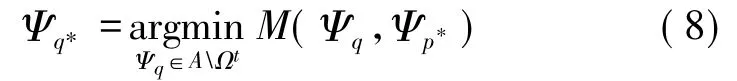
所定義的廣義相異性測度使不同目標點之間匹配效果的合理比較成為可能。

2.2 信度更新方式的修正

Criminisi算法在更新信度時，直接用C(p*)更新本次修復像素的信度。這樣做沒有考慮到本次模板匹配的精度，明顯有缺陷。我們將信度更新的方式修正為:

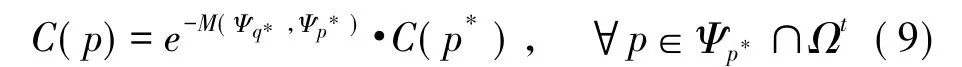
也即匹配效果越差，修復信度也應越小，反之亦然。

2.3 模板局部匹配搜索

Criminisi算法的時間代價主要是最優匹配模板的搜索。為了減小時間復雜度，我們采用局部搜索，也即將搜索區域限制在以當前待修復點為中心的一個窗口中。這樣做能使計算復雜度大幅減少，而修復精度的損失并不大。

3 實驗結果

本文在VC++下進行實驗，修復試驗包括全彩自然圖像的物體去除(object removal)以及已知圖像的修復仿真。處理器平臺為3GHZ的Pentium Dual-Core E5700 CPU。所有實驗中，PSmin設為 5×5，PSmax為17×17；局部搜索窗口大小定為51×51。需要說明的是，在計算邊界?Ωt上的像素點修復優先權時，我們采用固定的模板大小(9×9)。

3.1 修復效果比較

圖2～圖6是對幾幅自然圖像進行物體去除試驗的結果。圖2是經典的Bungee圖像，可以看出，改進算法在修復視覺效果方面有明顯提高。對照圖2(c)與圖2(d)，Criminisi算法修復結果中的贗像，譬如不連續的屋頂及延伸到水中的植被等通過改進算法基本得到消除。圖3和圖4分別是Criminisi算法和改進算法的修復過程。圖5與圖6是另外兩幅典型圖像的修復效果，改進算法都表現出類似的優越性。

圖2

圖3 Criminisi算法修復過程

圖4 改進算法修復過程

圖7是對已知圖像進行修復仿真實驗的結果。對這種情況還可計算修復客觀效果，也即結果圖像與原圖像間的PSNR，具體數據見表1，同樣證明了修復效果的提升。

圖5

圖6

圖7

3.2 時間復雜度比較

表1同時列出了Criminisi算法和改進算法的時間成本。可以看出，改進算法的時間復雜度也明顯比原算法低，綜合性能的改善十分顯著。

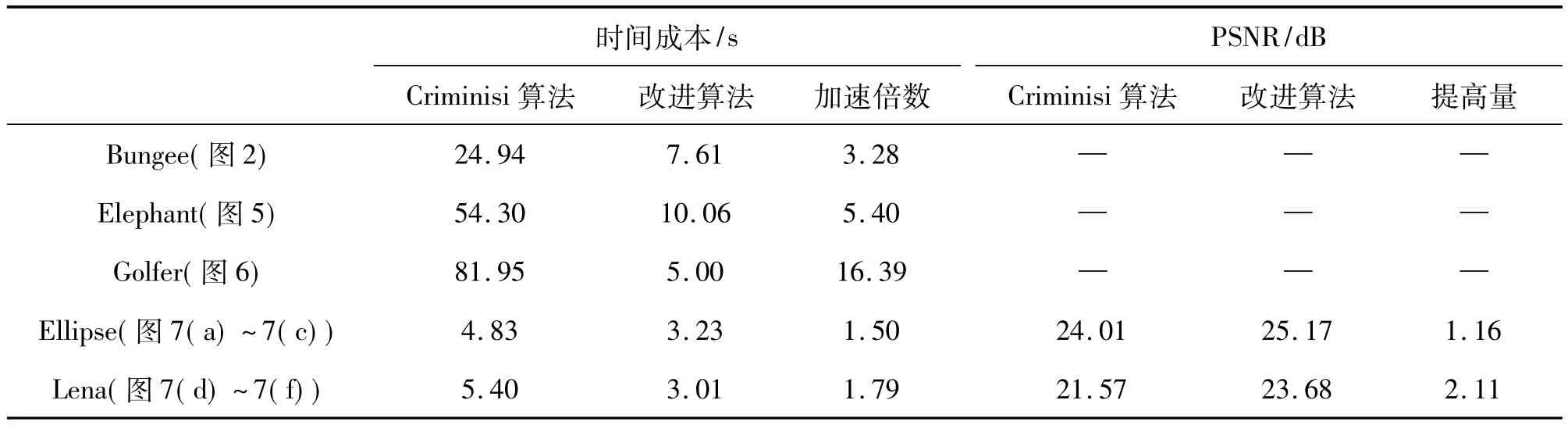
表1 時間成本和PSNR

4 結論

本文在保持Criminisi圖像修復算法基本框架不變的情況下，提出了一些較新穎的改進方案。我們的主要工作是設計了基于可變大小模板的高效塊匹配程序，并結合信度更新修正和局部搜索以提高算法的綜合性能。實驗結果表明了改進措施的有效性。

我們下一步的工作希望將改進方案與多分辨率修復框架［11－12］進行結合。此外，探索結合圖像結構的模板廣義相異性測度［8，13］和圖像分割［14］亦是很有意義的研究方向。

［1］Bertalmio M，Sapiro G，Ballester C，et al，Image Inpainting［C］//ACM SIGGRAPH，2000，417－424.

［2］Chan T，Shen J.Local Inpainting Models and TV Inpainting［J］.SIAM J.Appl Math，2001，62:1019－1043.

［3］Chan T，Shen J.Non-Texture Inpainting by Curvature Driven Diffusion(CDD)［J］.J Visual Comm Image Rep，2001，12(4):436－449.

［4］Chan T，Kang S，Shen J.Euler’s Elastica and Curvature Based Inpainting［J］.SIAM J Appl Math，2002，63(2):564－592.

［5］Efros A，Leung T.Texture Synthesis by Non-Parametric Sampling［C］//Proc IEEE Int Conf Computer Vision，1999，2，1033－1038.

［6］Criminisi A，Perez P，Toyama K.Region Filling and Object Removal by Exemplar-Based Image Inpainting［J］.IEEE Trans Image Process，Sep 2004，13(9):1200－1212.

［7］Komodakis N，Tziritas G.Image Completion Using Global Optimization［C］//Proc IEEE Computer Soc Conf Computer Vision and Pattern Recognition，2006，442－452.

［8］Bugeau A，Bertalmio M，Caselles V，et al，A Comprehensive Framework for Image Inpainting［J］.IEEE Trans Image Process，2010，19(10):2634－2645.

［9］Hsin H F，Leou J J，Lin C S，et al.Image Inpainting Using Structure-Guided Priority Belief Propagation and Label Transformations［C］//Pattern Recognition(ICPR)，2010 20th International Conference on，2010，4492－4495.

［10］Wohlberg B.Inpainting by Joint Optimization of Linear Combinations of Exemplars.Signal Processing Letters［J］.Signal Processing Letters，IEEE，2011，18(1):75－78.

［11］Fang C W，Lien J J.Rapid Image Completion System Using Multiresolution Patch-Based Directional and Nondirectional Approaches［J］.IEEE Trans Image Process，2009，18(12):2769－2779.

［12］蔡念，張海員，張楠.基于Contourlet的改進雙線性插值圖像超分辨率算法［J］.傳感技術學報，2011，24(1):59－64.

［13］朱良銷，余學才，陳濤，等.一種擴展動態范圍的圖像處理算法［J］.傳感技術學報，2011，24(1):65－67.

［14］Ojeda S，Vallejos R，Bustos O.A New Image Segmentation Algorithm with Applications to Image Inpainting［J］.Comput Stat Data Anal，2010，54(9):2082－2093.