基于混沌思想的可多步搜索的新型粒子群優化算法
林博藝
(泉州信息職業技術學院,福建 泉州 362000)
基于混沌思想的可多步搜索的新型粒子群優化算法
林博藝
(泉州信息職業技術學院,福建 泉州 362000)
針對基本PSO算法在全局優化中收斂精度低和易陷入局部極值的不足,提出一種基于混沌思想的多步搜索的新型的粒子群優化算法(CMPSO).該算法先引入混沌思想對粒子種群進行位置初始化,然后再引入多步搜索,最后引入概率條件的選擇性重新初始化.通過與其它三個改進算法比較,結果表明CMPSO算法的有效性.
粒子群優化;多步搜索;混沌
1995年Kennedy博士和Eberhart教授提出粒子群優化(Particle Swarm optimization,PSO)算法[1,2],它是一種基于群體智能(Swarm Intelligence,SI)仿生的優化方法,該算法基本思想是源于對鳥群捕食行為的模擬.由于其原理簡潔,參數較少,易于實現等優點,成為繼遺傳算法后的研究熱點之一.其已被廣泛的應用于函數優化[3],工程優化[4],參數估計[5-9],電力系統優化[10-14],控制器設計[15-7],機器人路徑規劃[8]等.
類似于GA,PSO算法也有收斂精度低,早熟等不足[18-20],因此繼Kennedy和Eberhart之后有許多改進型PSO算法提出.如:引入慣性權重,加入微分演化或是交叉操作,加入混沌初始化,與其它智能算法混合等,這些算法在增加算法得雜度的前提下,都不同程度的提高算法的性能.但這樣做都有悖于算法的初衷:簡潔實效.本人在分析基本PSO算法不足的基礎上,引入混沌初始化,并將多步式位置更新引入其中,并通過實驗來驗證我們改進的有效性.
1 PSO簡介
一個有N個粒子的種群,在D維空間中進行尋優過程的算法的基本遞推公式:

其中:i=1,2,…,N;d=1,2,…,D;Xid(k+1),Xid(k),Vid(k+1),Vid(k)分別表示第 i個粒子在 k+1 和 k代的空間位置對應的第d維值及運動速度對應的第d維值;ω為慣性權重;c1,c2分別表示粒子個體和粒子群體的加速權重系數;r1,r2均為0到1之間的隨機值,分別表示粒子個體和全體的加速權重;Pid與Pgd分別表示第i個粒子個體在搜索過程中自身的歷史最佳位置和整個粒子群體目前找到的最佳位置.
2 新的PSO算法
2.1 PSO算法陷入局部收斂的原因
基本PSO算法易陷入局部極值的原因在文獻[3]做了詳細的分析,并通過數學推導得到式(3):
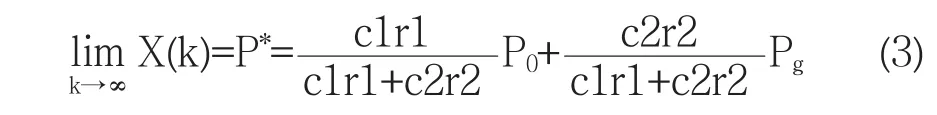
由式(3)可知,每個粒子不僅受它自己找到的當前最優解的吸引,而且還受全局最優解的吸引.如果這兩個最優解都是局部最優值,粒子將被這兩個值吸引而很快重復相同的搜索軌跡.由于式(1)沒有使算法跳出局部最優的機制,隨著進化迭代的進行,粒子最終將聚集到由個體極值位置P0和全局極值位置Pg共同決定的位置P*上,如果P*是某個局部最優位置,且所有粒子在向位置P*靠攏的過程中若沒有找到優于Pg的位置,則基本PSO的進化過程將很難跳出該局部最優,粒子將逐步收斂到P*.另外,結合式(1)還可看出,慣性權重僅能改變粒子的搜索步長,不能改變其運行方向,從而不能克服早熟問題.可見,加強搜索多樣性、使算法跳出局部最優,是提高算法收斂速度和尋優精度的重要措施.本文從以下三個方面入手,提出一種基于混沌思想和多步搜索的PSO算法.
2.2 初始化粒子群初始位置
混沌序列的運動特點:隨機性和遍歷性及規律性.本文采用混沌序列的這一特點對粒子進行初始化分布,這樣可以更好的體現初始種群的多樣性,為在尋優空間中找到最優解和加快收斂速度奠定較為堅實的基礎.
Logistic映射是一個典型的混沌系統,首先利用Logistic映射產生混沌序列,如式(4):
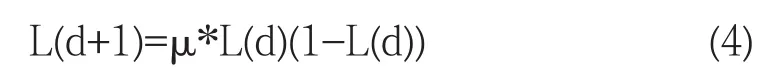
式(4)中 μ 為一個常數,μ∈[3.56,4.0],稱為控制參量,主要用來控制系統的混沌程度,L(d)∈(0,1),d=1,2,3,…,D.
第二步對處于D維中間中的N個粒子,首先產生 N 個初始值:L1(1),L2(1),…,Li(1),…,LN(1),把這N個初始值代入式(4)中進行D次迭代運算,將產生的結果代入式(5)中運算:
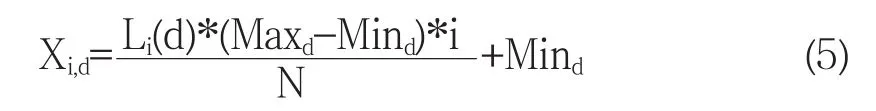
式(5)中:Xi,d表示第i個粒子第d維坐標,而Li(d)是第i個粒子用Li(1)經過d次迭代運算產生的值,Maxd,Mind分別是第d維的上下限.
2.3 引入多步搜索
由公式(1)知,粒子的運動失量由慣性項Vid(k),自身認知成分項c1*r1*(Pid-Xid(k)),社會認知成分項c2*r2*(Pgd-Xid(k))三項決定的,受人類活動行為的啟發可知:人類在做事時,有時會慣性式的執行,有時會加以總結靠自身的經驗,有時卻也會對所有信息加以匯總考慮然后再去做事(基本PSO算法則是這種方式)[19].本文在盡量不增加PSO算法的基礎上,對運算過程中的三項結果直接加以分析迭代:

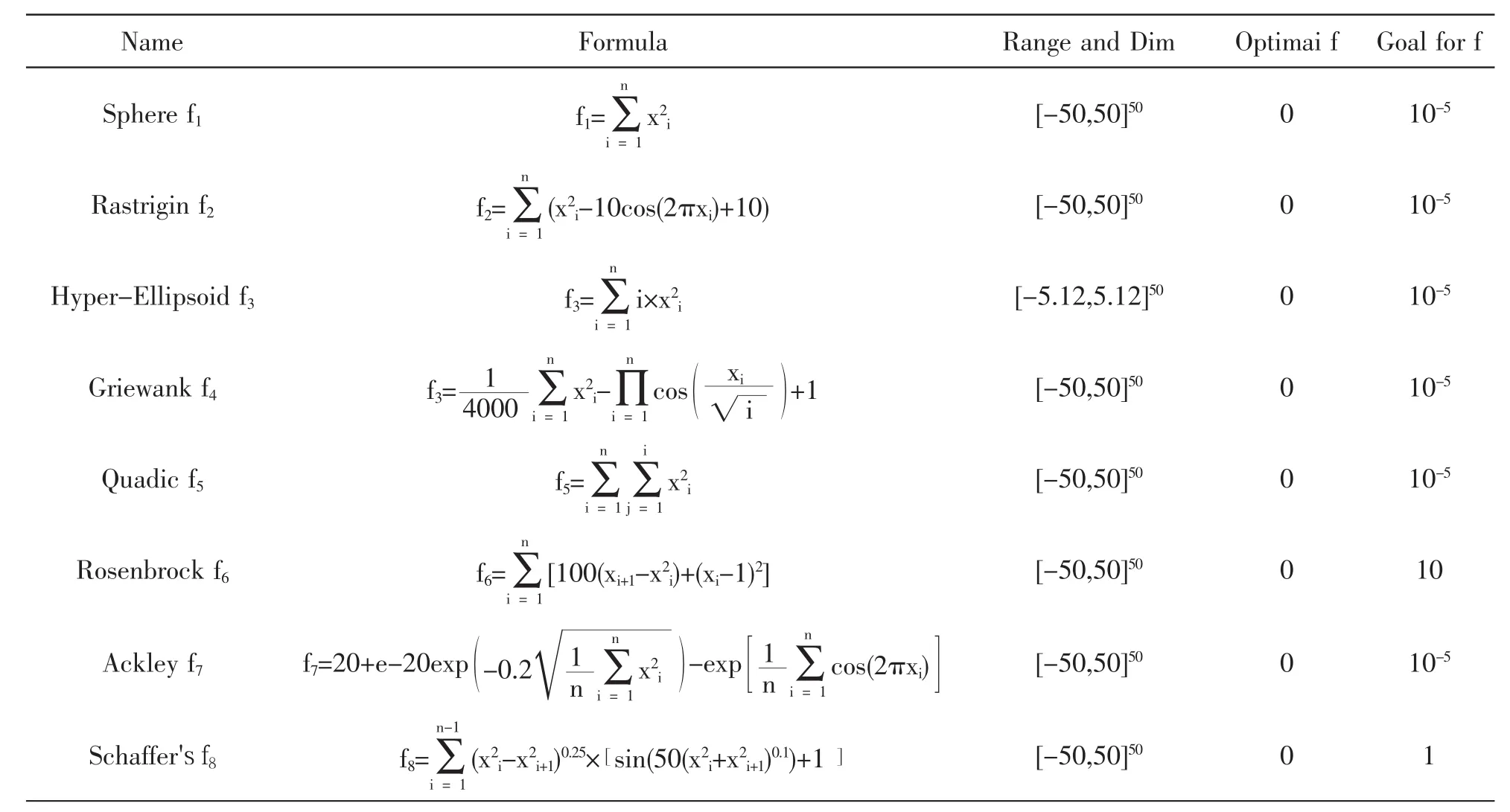
(6)Xid(k+1)3=Xid(k)ω*Vid(k)+c1*r1*(Pid-Xid(k)) (7)Xid(k+1)2=Xid(k)+ω*Vid(k)Xid(k+1)new=!###"###$Xid(k+1)2 if(f(Xid(k+1)2)) 由式(8)可知,粒子在搜索過程中,先利用自身慣性做第一步位移Xid(k+1)2,如果此步位移得到搜索位置最好,則取之;否則進一步利用自身認知經驗項得到位移點Xid(k+1)3,同進也可再利用社會認識經驗得到 Xid(k+1).最后比較 Xid(k+1),Xid(k+1)2,Xid(k+1)3,取其最優者做為下一步的運動位置更新點. 綜上所述,改進的PSO算法具有PSO算法的基本特點,簡單,易實現,運算量較小等優點,同時兼顧了搜索效率和收斂精度,此外,新算法并未引入新的參數,這樣就易于通用,因為新算法將搜索的中間值加以利用和分析,省去了參數調節的煩瑣計算,因此新算法較簡單通用. 在粒子群的進化過程中,當得到的最優解在連續的M次迭代中都無變化時,用一個計數器記錄到目前為止停滯的代數T,可以這樣設定:如果連續兩次得到的最優解相同則將T增1,否則將其清0;當T≥M時,則說明算法可能停滯,在M次的迭代中,粒子沒有能力跳出局部最優.此時,為加強粒子的對空間的搜索可以對某些粒子在概率性選擇下進行隨機重新初始化.搜索空間區域為:[XMind,XMaxd],在其內部重新初始化即為: 其中:β為事先設定的一個閾值,可取[0.8,1]. 在迭代過程中,當粒子有可能陷入局部極值時,為避免過大的破壞粒子原有的運行狀態,僅選擇少部分粒子進行重新初始化. 選用4個典型基準測試函數,與基本PSO及sPSO[18[18],HPSO-TVAC[15]等算法比較,驗證CMPSO的可行性.這4個常用的基準函數、函數形式、搜索范圍及維數、理論極值(極小值)和優化目標精度等見表1;其中:HPSO-TVAC,sPSO和tPSO參數設置與文獻[18]與文獻[15]一致,CMPSO參數設 置 為 :ω0=1.2,c1=c2=2,ω=ω0*exp(-0.5*k*k),μ=3.99,Max=10,β=0.8. 對算法性能評估采用如下方法[18]:(1)固定迭代次數下的實驗效果對比;(2)固定收斂精度的實驗效果對比. 固定代數下的的實驗結果對比如圖1所示,實驗結果是采用獨立運行50次后的平均值給出.其中:粒子數目為50,進化代數為1000;圖1(a)~圖1(h)是五種算法分別在測試函數f1~f8的適應度值的對數曲線(為方便顯示統一加10-10做為適應度的截止值). 從圖1-1(a)到圖1-1(h)可以看出,PSO算法在1000代內都難以收斂到目標精度,其他改進算法表現在總體上均優于PSO算法.下面依次詳細分析. 從圖1-1中可以看出,CMPSO算法較其它四中算法均得到較大改進,對8個函數的優化來看基本上在100代以內都能收斂到目標精度,有的函數甚至在20代以內都能收斂到目標精度,可以說CMPSO算法表現是較其它算法是最佳的.其它算法中sPSO,再次是tPSO算法收斂情況較好.在對Rosenbrock函數f6(一個經典的復雜優化問題,取值區間內平坦,為算法提供了少量的信息,要收斂到全局最優位置的機會非常小,所以它一般用來測試算法的執行效率[19])及Schaffer’s函數f8這兩個函數上,CMPSO將其改進后的開求精能力和開挖能力充分表現出來:如Rosenbrock函數f6,其在400代后又進一步向高精度深度求精;在Schaffer’s函數f8表現更為明顯,在1000代以內不斷向更高精度逼進,充分體現了其對空間的開挖能力和求精能力. 表1 8個基準測試函數 圖1-1 f1~f8在5個實驗中的適應度值進化曲線 表2 實驗結果對比 因此,CMPSO算法改善了PSO算法對空間的全局搜索效果,提高了算法的收斂速度和精度,較為有效的避免了早熟問題,與其它改進算法相比也是有較大的改進,如:較tPSO算法參數少,更具有通用性;較sPSO收斂速度和精度也有較大的提高.因此,在固定迭代次數的前題下,CMPSO算法改進有效性得到有力證實. 作如下規定:同樣是種群規模為50,在表1指定的收斂精度下,對達到收斂精度所需的迭代次數進行比較.由達到目標精度的最小值,均值,最大值,方差等方面加以考察.表2是由表1指定精度下獨立50次所得 (如果算法在10000代內還沒有收斂到目標精度于以終止). 由表2可見:在收斂速度上PSO算法最差,其次是HPSO-TVAC,這兩個算法在大部分情況下不能收斂到目標精度,而其它三種算法基本上均能收斂到目標精度.CMPSO在固定收斂精度下,其收斂速度均優于其它算法,而sPSO在收斂速度上優于tPSO,三者中CMPSO表現最佳,說明了改進有效性. 本文在分析基本PSO算法收斂精度低,早熟等不足的基礎上,受自然現象的啟發,提出了一種改進型的PSO算法.用經典的測試函數來測試算法,經驗證,充分表明了改進算法的有效性. 〔1〕Kennedy J,Eberhart R C.Particle swarm optimization [C].In:Proc.of the IEEE Internationa1 Conference on Neura1 Networks,Perth,Australia.1995,1942-1948. 〔2〕ShiY,EberhartR C.A modified particle swarm optimizer [C].In:Proc.of the IEEE International Conference on Evolutionary Computation.1998,69-73. 〔3〕Clerc M,Kennedy J.The particle swarm:Explosion stability and convergence in a multidimensional complex space[J].IEEE Trans.on Evolutionary Computation.2002,6(1):58-73. 〔4〕武忠勇,緱錦,趙志強.具有自適應鄰域探測機制的改進型PSO算法[J].小型微型計算機系統,2010,31(9):1938-1945. 〔5〕鄭宣耀,李歡,滕少華.自適應變鄰域混沌搜索微粒群算法 [J].計算機工程與應用,2007,43(31):90-93. 〔6〕趙娜,張伏生,魏平,等.基于改進多粒子群算法的電力系統無功優化 [J].西安交通大學學報,2006,34(4):463-467. 〔7〕張勇,鞏敦衛,張婉秋.一種基于單純形法的改進微粒群優化算法及其收斂性分析[J].自動化學報,2009,35(3):289-298. 〔8〕Parsopoulos K E,Vrahatis M N.UPSO:A unified particle swarm optimization scheme[C].In:Proc.of the ICCM SE 2004.Attica.2004:868-873. 〔9〕Mendes R,Kennedy J,Neves J.The fully informed particle swarm:Simpler,maybe better[J].IEEE Trans.on Evolutionary Computation.2004,8(3):204-210. 〔10〕赫然,王永吉,王青,等.一種改進的自適應逃逸微粒群算法及實驗分析 [J].軟件學報,2005,16(12):2036-2044. 〔11〕Peram T,Veeramachaneni K.Fitness-Distance-Ratio based particle swarm optimization[C].In:Proc.of the IEEE Swarm Intelligence Symp.Indianapolis.2003,174-181. 〔12〕〔13〕Trelea IC.The particle swarm optimization algorithm:Convergence analysis and parameter selection [J].Information Processing Letters.2003,85(6):317-325. 〔14〕潘峰,陳杰,甘明剛,等.粒子群優化算法模型分析[J].自動化學報,2006,32(3):368-377. 〔15〕Ratanaweera A,Halgamuge S K,Watson H C.Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients [J].IEEE Trans.on Evolutionary Computation,2004,8(3):240-255. 〔16〕Liang J J,Qin A K.Comprehensive learning particle swarm optimizer for global optimization of multimodal functions[J].IEEE Trans.on Evolutionary Computation,2006,10(3):281-295. 〔17〕呂艷萍,李紹滋,陳水利,等.自適應擴散混合變異機制微粒群算法 [J].軟件學報,2007,18(11):2740-2751. 〔18〕胡旺,李志蜀.一種簡化而高效的粒子群優化算法[J].軟件學報,2007,18(4):861-868. 〔19〕高芳,崔剛,吳智博,等.一種新型多步式位置可選擇更新粒子群優化算法 [J].電子學報,2009,37(3):529-534. 〔20〕紀震,周家銳,廖惠連,等.智能單粒子優化算法[J].計算機學報,2010,33(2):556-561. TP18 A 1673-260X(2012)10-0015-052.4 重新初始化
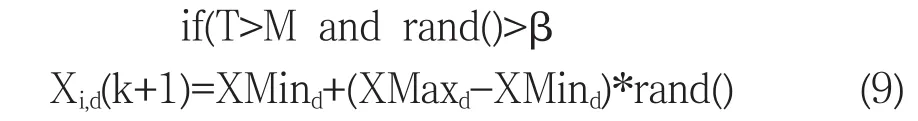
3 實驗及結果分析
3.1 實驗設計
3.2 實驗結果分析
3.2.1 固定迭代次數下的實驗效果對比
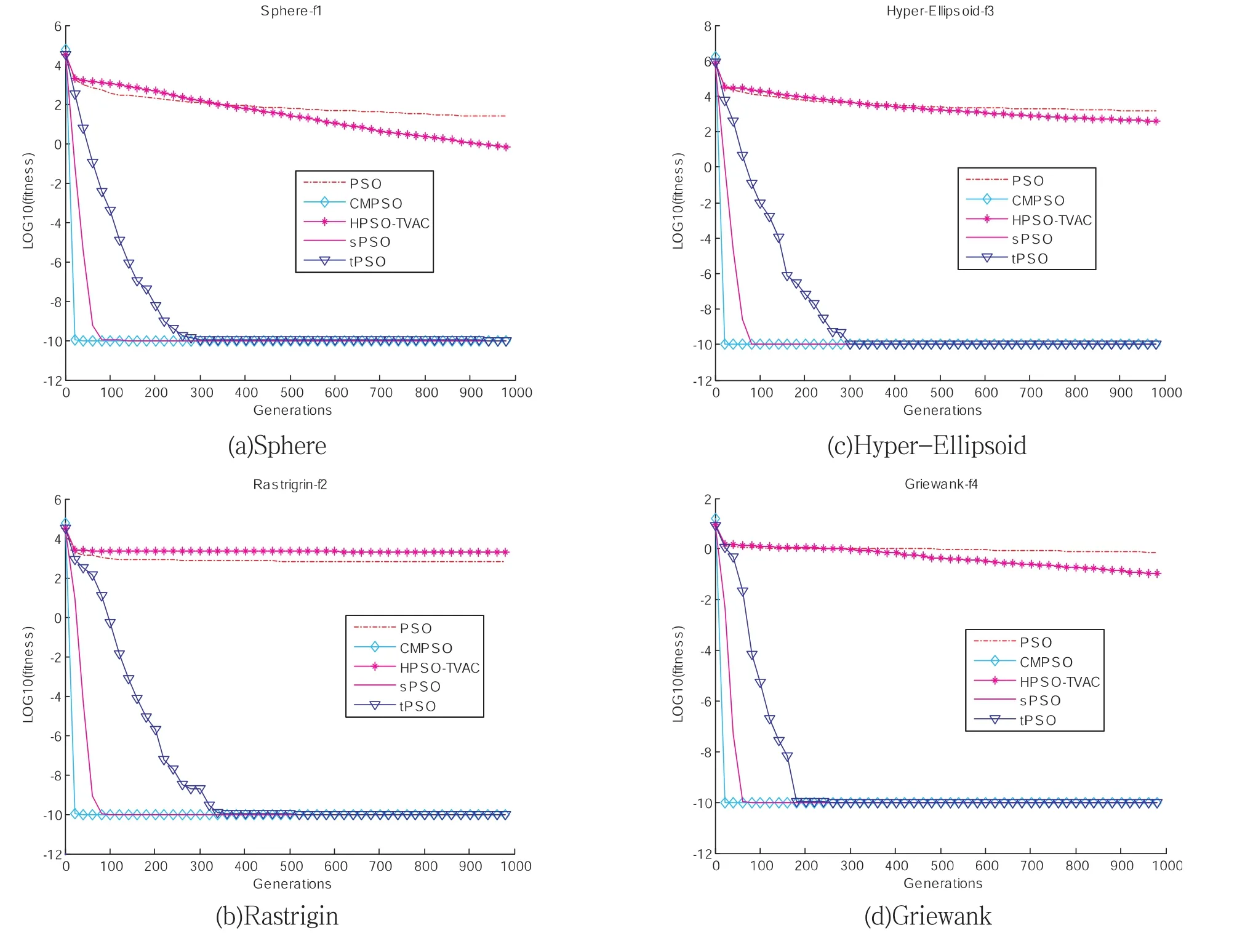
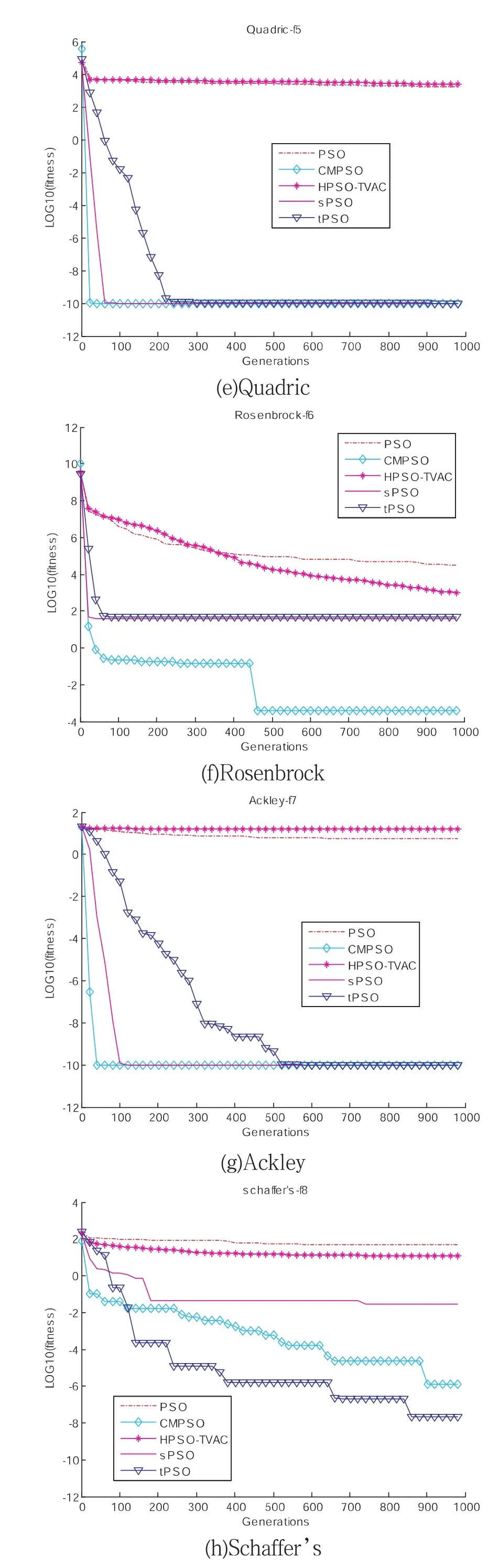
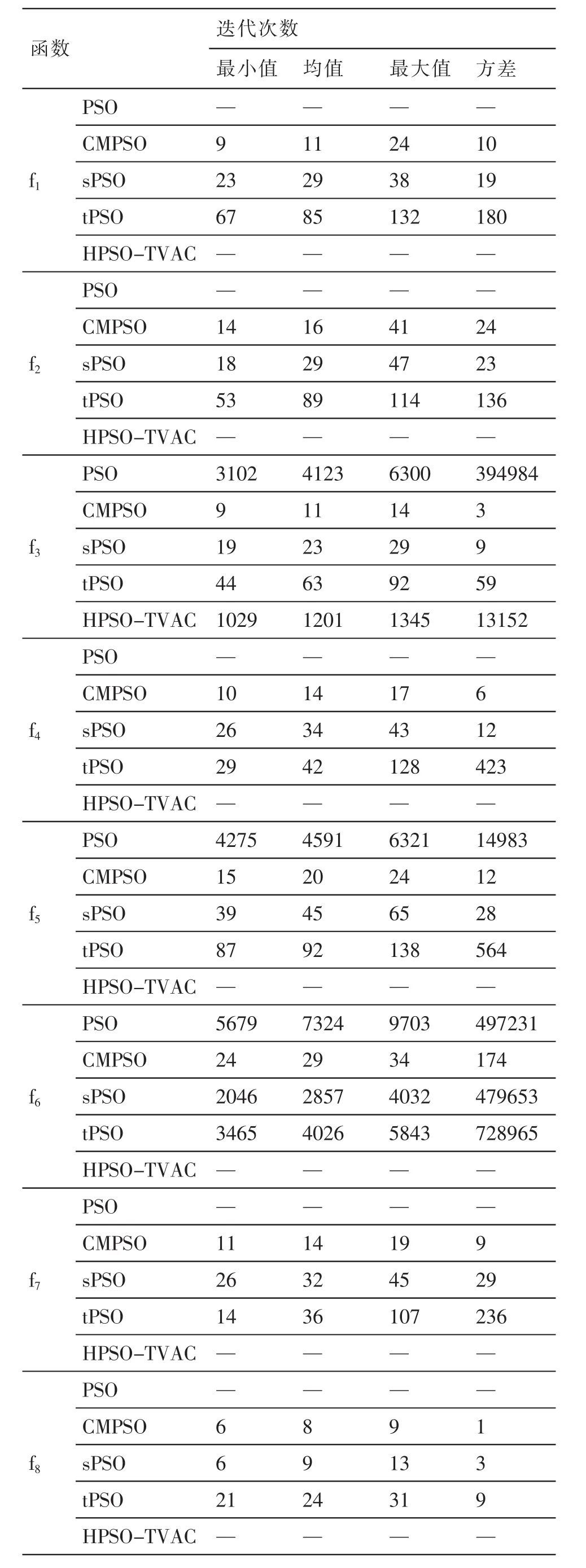
3.2.2 固定收斂精度的實驗效果對比
4 總結

