半群的Cwrpp Rees根的擴張結構

高振林， 許成蘇

（上海理工大學 理學院，上海 200093）

1 預備知識

定義1［1］半群S上的Green′s關系L和R定義為

Fountain［2］將Green’s關系推廣，定義 Green’s＊關系L＊和R＊為：

（a，b）∈L＊當且僅當對?x，y∈S1有ax＝ay?bx＝by

（a，b）∈R＊當且僅當對?x，y∈S1有xa＝ya?xb＝yb

文獻［3］對Green′s＊－關系做了進一步推廣，定義Green’s＊＊關系L＊＊和R＊＊為

（a，b）∈L＊＊當且僅當對?x，y∈S1有（ax，ay）∈R?（bx，by）∈R

（a，b）∈R＊＊當且僅當對?x，y∈S1有（ax，ay）∈L?（bx，by）∈L

定義2［4］半群S如果滿足下列條件：

a.S的每個L＊＊－類至少含有一個冪等元；

b.對?a∈S，?e∈E（）有a＝ae，其中E（）為的冪等元集合，則稱S為wrpp半群；若wrpp半群S還滿足E（S）?C（S），即S的冪等元在S的中心（）CS中，則稱S為Cwrpp半群.

定義3［5］半群S上的同余ρ稱為Cwrpp同余，如果S／ρ是Cwrpp半群.此時如果ρ還是S上的Rees同余，稱ρ是Cwrpp Rees同余.

定義4［5］對半群S上的Cwrpp同余ρ，如果存在S的子集I和Cwrpp子半群使得

S＝I∪C（不必是不交并）且C?S／ρ

則稱I是S的（Cwrpp）ρ－集，這時將ρ記作ρI.

由文獻［5］知，若（Cwrpp）ρ－集存在，則由ρ唯一確定.另外，若ρ是 Cwrpp Rees同余，則（Cwrpp）ρ－集I必存在，且I是半群S的理想，稱I為S的Cwrppρ－理想.

定義5［5］對半群S，如果S無任何Cwrpp同余，那么定義S的Cwrpp根同余是泛關系S×S，且稱S是Cwrpp根半群；如果S至少有一個Cwrpp同余，那么定義S上的Cwrpp根同余是所有Cwrpp同余ρα（α∈w）的交，記作ρcr.即

如果ρcr也有ρcr－集，則將其記為N（S）.即ρcr＝ρN（S）.稱N（S）為S的 Cwrpp根集.對于 Cwrpp根同余ρcr和Cwrpp根集N（S），有時統稱它們為S的Cwrpp根.

由定義5知，對任－半群S，ρcr總是存在的.一般地，ρcr不必仍是S的Cwrpp同余.當然，若ρcr仍是S上的Cwrpp同余，那么ρcr是S上的最小Cwrpp同余.

定義6［5］稱半群S的Cwrpp根同余ρcr是強Cwrpp根，若ρcr仍是S上的Cwrpp同余，且N（S）存在.若S的強Cwrpp根同余ρcr還是Rees同余，即N（S）是S的理想，則稱S為有強Cwrpp Rees根的wrpp半群.

設半群S的Cwrpp根同余ρcr是強Cwrpp根，由文獻［5］知

定義7［4］稱半群S為（右）左（L）R－可消的，若?a，b，c∈S有（（ba，ca）∈L?（b，c）∈L）（ab，ac）∈R?（b，c）∈R.

定義8 假設N，T＊是不相交半群，T＝T＊∪｛0｝有零元0.稱半群S是由T關于N的一個（理想）擴張，如果S＝NT＊（不交并）且N是S的一個理想使得S／N?T.T關于N的一個（理想）擴張S稱為Cwrpp Rees根的擴張，若T是Cwrpp半群且N（S）＝N是wrpp半群.

文獻［5］解決了有強Cwrpp根且N（S）＝E（S）是帶的wrpp半群S（即SBCRW－半群）的結構刻畫.本文繼文獻［5］的工作，用半群的理想擴張基本理論證明Cwrpp Rees根的擴張半群的結構特征，給出半群Cwrpp Rees根的幾種擴張結構.

2 基本性質

由文獻［1，3］得以下性質：

性質1 a.（R＊＊－關系）L＊＊－關系為任意半群S上的（左同余）右同余，且在S上有（R＊?R＊＊，R＊＊｜E（S）＝R.）L＊?L＊＊，L＊＊｜E（S）＝L；

b.設U是半群S的子半群，則 LU?LS∩（U×U），RU?RS∩（U×U）.

由定義3，4，8易得以下引理1，2與性質2.

引理1 若ρ是半群S上的Cwrpp Rees同余，則必有S的Cwrppρ－理想I使得ρ＝（I×I）∪1S且S／ρ同構于Cwrpp半群S＼I∪｛0｝.

引理2 半群S的Cwrpp根同余ρcr是強Cwrpp Rees根同余的充分必要條件為：

a.ρcr是Cwrpp同余；

b.N（S）存在且N（S）是S的理想.

性質2 設S是有強Cwrpp Rees根的wrpp半群，則

a.N（S）是Cwrpp根半群；

b.如果I既是S的Cwrpp理想，又是Cwrpp根半群，那么I＝N（S）；

c.S是Cwrpp Rees根的擴張半群.

證明 只要證明c.設S滿足題設要求，N＝N（S）是S的Cwrpp Rees根，由引理1，知

C＝∪α∈YMα∪ ｛0｝，S／N?S＼N∪ ｛0｝＝C是Cwrpp半群.依定義8，S是Cwrpp Rees根的擴張半群.證畢.

性質3［3］有零元的Cwrpp半群C＝C＊∪｛0｝有半格分解表示

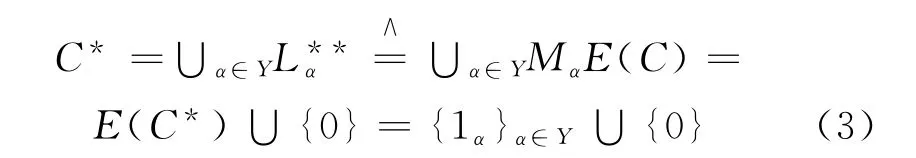
性質4［3］設S是有強Cwrpp Rees根的 wrpp半群.若E（S）是帶，則存在半格Y使得E（N（S））包含子帶

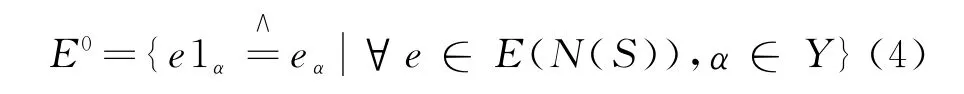
證明 由題設條件和引理2得，S／N（S）?S＼N（S）∪｛0｝是Cwrpp半群，由性質3，設S＼N（S）∪＼是左R－可消么半群的半格，這里Y是半格，1α是（α∈Y）的恒等元.因為E（S）＝E（N（S））∪｛1α｝α∈Y是帶，N（S）是S的理想，故對e∈E（N（S）），1α∈C＊，e1α，1αe∈E（N（S）），于是e1α·e1α＝e1α＝eα，e1αf∈E（N（S））.則對?eα，fβ∈E0（由式（4）定義），eα·fβ＝e1α·f1β＝h1β＝hβ∈E0（h＝e1αf）.即E°是E（N（S））的子帶.證畢.

性質5 Cwrpp Rees根的擴張半群S是有強Cwrpp Rees根的wrpp半群.

證明 只要證S是wrpp半群，則由定義8即知S是有強Cwrpp Rees根的wrpp半群.設a∈這里C是Cwrpp半群且N（S）＝N是wrpp半群.往證定義2中a與b.

若α∈N，因N是wrpp半群，故有冪等元e∈E（N），эeL＊＊Na且對?f∈E（N））有a＝af.由定義1，對

?x，y∈N，（ax，ay）∈RN?（ex，ey）∈RN

設x，y∈S，（ax，ay）∈RS＝R，則有x，，y，∈S，∈ax＝ayy，，ay＝axx，.于是

axN＝ayy，N?ayN，ayN＝axx，N?axN從而axN＝ayN，即（ax，ay）∈RN.由上式推得（ex，ey）∈RN，再由性質1得（ex，ey）∈RS.同理可證（ex，ey）∈RS?（ax，ay）∈RS.綜合得（a，e）∈L＊＊S.設?f∈E（（S）），因

E（S）＼｛0｝＝E（N）∪E（C＊），C＊＝C＼｛0｝若f∈E（（N）），由上知a＝af；若f＝1α∈E（C＊）（?α∈Y），由（f，e）∈L＊＊S和性質1得eS1＝fS1.因為e∈N，f∈C＊且N是S的理想，故eS1?N，fS1∩C＊≠Φ.從而eS1≠fS1.

這表明不存在α∈Y，f＝1α∈E（C＊）∈f∈E（（S））.故對α∈N定義2中a與b成立.

對α∈C用以上相同方法可得定義2中a與b成立.證畢.

由性質2與性質5得：

定理1 設S為半群，以下兩條等價.

a.S是Cwrpp Rees根擴張半群；

b.S是有強Cwrpp Rees根的wrpp半群.

引理3［6］設半群C與I滿足以下兩條，則C關于I的擴張總是存在的.

a.C無真零因子；

b.I至少有一個冪等元.

3 半群的Cwrpp Rees根的擴張結構

用半群的理想擴張基本理論，給出半群的幾種Cwrpp Rees根的擴張結構定理.

首先C＝C＊∪｛0｝是由式（3）給定的有零元的Cwrpp半群，N是與C＊不相交的Cwrpp根wrpp半群.E（N）包含由Y決定的半格

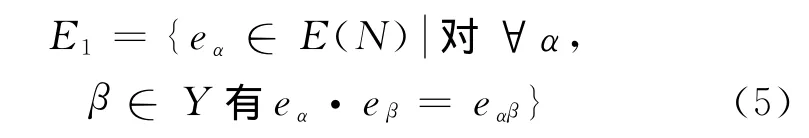
定理2 從C＊＝∪α∈YMα到N的映射θ定為

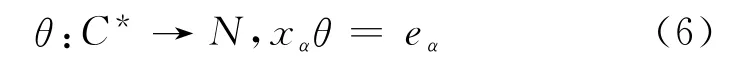
則以下結論成立：

a.θ是一個局部同態映射［6］；

b.令S＝NC＊為不交并，在S上定義由（a）－（d）決定的運算“。”

（a）?x，y∈C＊，x?y＝xy在C＊中；

（b）?x∈C＊，n∈N，x?n＝xθ·n在N中；

（c）?x∈C＊，n∈N，n?x＝n·xθ在N中；

（d）?n，m∈M，n?m＝nm在N中.

則S構成一個Cwrpp Rees根的擴張半群.

證明a.首先指出θ是C＊到N的局部同態.只需證明對任意的xα∈Mα，yβ∈Mβ有 （xαyβ）θ＝xαθyβθ成立.由θ的定義知，存在eα，eβ∈E1使得xαθ＝eα，yβθ＝eβ.因C＊是Cwrpp半群，E1是由Y決定的半格，故有

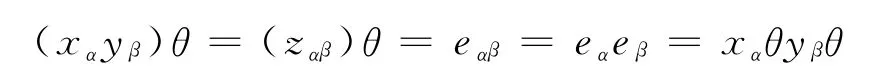
b.由文獻［6］知，S是θ決定的C關于N的擴張.因為N是Cwrpp根wrpp半群，C是Cwrpp半群，S＝NC＊，故N是S的最小Cwrpp理想，所以N＝N（S）.即S構成Cwrpp Rees根的擴張半群.證畢.

由文獻［4－5］，性質3和定理2得以下推論：

推論1 設C是由式（3）給出的Cwrpp（Crpp）半群，N是Cwrpp根wrpp半群且有半格分解N＝∪α∈Y.若N∩C＊＝Φ，則

a.E（N）是帶且包含子半格E1（式（5）定義）；

b.從C＊到N可由式（6）定義局部同態映射θ，通過（M1）－（M4）決定C關于N的Cwrpp（Crpp）Rees根擴張半群S，使得N是S的強Cwrpp（或Crpp）Rees根.

以上推論的一個特別情形是下面的結論：

推論2 設C為式（3）給出的Cwrpp（Crpp）半群，N是有零元的左（右）正則帶.若N∩C＊＝Φ，則

a.N是包含子半格E1（如式（5）定義）的Cwrpp根wrpp半群；

b.從C＊到N可由式（6）定義局部同態映射θ，通過（a）－（d）決定C關于N的Cwrpp（Crpp）Rees根擴張半群S，使得N是S的強Cwrpp（或Crpp）Rees根.

由性質4，Cwrpp根wrpp半群N的冪等元集E（N）不必包含子半格E1.但只要E（N）非空，由引理3知，N的Cwrpp Rees根擴張總是存在的.因此類似定理2的證明，易證下列更一般的Cwrpp根擴張定理.這里省略其證明.

定理3 設N是有零元的Cwrpp根wrpp半群，Cwrpp半群C由式（3）給出，S＝N∪·C＊是不交并.若有e∈E（N），則映射θ：?x∈C＊，xθ＝e是局部同態映射，且S關于運算“。”（由（a）－（d）給出）構成C關于N的Cwrpp Rees根擴張半群.

對E（N）中兩個不同的冪等元，由定理3可以得到兩個C關于N的Cwrpp Rees根擴張.兩者之間的關系由文獻［6］給出：

定理4 半群N，C如定理3所設.若有e，f∈E（N），e≠f，則

a.可確定兩個C＊到N的局部同態映射θ，θ′為

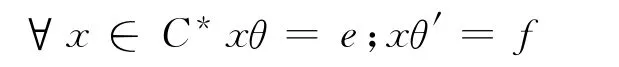
由θ，θ′可分別決定N的兩個Cwrpp Rees根擴張半群S，S′；

b.S和S′是等價擴張（見文獻［6］）當且僅當存在N的自同構φ和C的自同構φ，使得θφ＝φ1θ′，其中φ1＝φ｜C＊.

4 例 子

最后用下例結朿本文，該例指出Cwrpp Rees根的擴張半群（即有強Cwrpp Rees根的wrpp半群）有其獨特意義.

例1設C是有零元的Cwrpp半群，C的半格分解表示由式（4）給出.取N＝Y＝E1（見式（5）），則N為半格，對任意的x∈C＊，存在α∈Y使得x＝xα∈Mα.可定義映射

下證θ為C＊到N上的局部同態映射.

對x，y∈C＊，則存在α，β∈N使得x∈Mα，y∈Mβ，因此不妨記x＝xα，y＝yβ.則存在zαβ∈Mαβ，使得

（xα·yβ）θ＝ （zαβ）θ＝αβ＝ （xαθ）·（yβθ）故θ為C＊到N的局部同態映射.又對α∈N，?xα∈Mα，?xαθ＝α，即θ為C＊到N上的局部同態映射.令S＝C＊∪N為不交并，S上的運算“。”由（a）－（d）給出，即

?x，y∈C＊，x?y＝xy在C＊中

?x∈C＊，β∈N，x?β＝xθ·n＝αβ在N中

?x∈C＊，β∈N，β?x＝β·xθ＝βα在N中

?α，β∈N，α?β＝αβ在N中

由定理2知，S是一個Cwrpp Rees根的擴張半群.它是有強Cwrpp Rees根N的wrpp半群.

由于E（S）＝E（N）∪｛1α｝α∈Y＝N∪｛1α｝α∈Y，按以上“。”運算定義有

即E（S）為半格.由于E（S）≠N（S）＝N，故S不是文獻［5］中的SBCRW－半群.由文獻［5］知，左Cwrpp（右Cwrpp），完備rpp半群（見文獻［4，7］）均是SBCRW－半群，故S不是這幾類半群中的任何一類.

［1］Howie J M.An introduction to semigroup theory［M］.London：Academic Press，1976.

［2］Fountain J B.Abundant semigroups［J］.American Mathematical Society，1982，44（3）：103－129.

［3］Tang X D.On a theorem of C－wrpp semigroups［J］.Communications in Algebra，1997，25 （5）：1499－1504.

［4］Lan Du，Shum K P.On left C－wrpp semigroups［J］.Semigroup Form，2003，67（3）：373－387.

［5］高振林，宋土芳.半群的C－wrpp根和半C－wrpp半群［J］.上海理工大學學報，2012，34（5）：499－504.

［6］Clifford A H，Preston G B.The algebraic theory of semigroups［M］.Providence：American Mathematical Society，1961.

［7］Guo X J，Shum K P，Guo Y Q.Perfect rpp semigroups［J］.Communications in Algebra，2001，29（6）：2447－2459.