屏蔽電機主泵慣性飛輪完整性分析

葛 磊， 王德忠， 張繼革

（上海交通大學 機械與動力工程學院，上海 200240）

屏蔽電機主泵是單級、全密封、高慣量離心式屏蔽泵，用來輸送高壓、高溫、大流量的反應堆冷卻劑［1］.在主泵電機的轉軸上安裝飛輪，是為了保證主循環泵在反應堆緊急停堆或全廠斷電事故下，仍能提供一定的惰轉流量，繼續驅動冷卻劑循環，冷卻堆芯，從而為緊急停堆操作提供必要的緩沖時間.因此，飛輪的結構完整性直接關系到整個反應堆系統的安全性.為保證主泵在停堆后具有足夠的惰轉能力，從而保證堆芯的正常冷卻，有必要對主循環慣性飛輪的完整性進行分析.國內外對軸封泵飛輪完整性有了一定的研究［2－6］，但對屏蔽泵飛輪的完整性未進行深入的研究.鑒于此，本文主要工作是對屏蔽電機主泵的飛輪完整性進行分析.筆者首先對飛輪模型作了一定的簡化和假設，即未考慮鎢合金扇形塊之間的相互作用，并通過解析法計算出飛輪的應力位移分布.然后運用有限元軟件ANSYS對飛輪結構完整性進行分析，有限元建模時考慮鎢合金扇形塊之間的相互作用，得出飛輪的應力、位移分布.將解析解與ANSYS分析結果進行對比，從而驗證解析解中的簡化和假設的合理性，并證明了方法的正確性和可行性.最終利用分析結果判定飛輪結構的完整性.

1 飛輪設計與要求

1.1 飛輪結構

飛輪的結構是將鎢合金扇形塊裝到實心內輪轂上，利用厚壁的外輪轂夾持扇形塊.依靠外輪轂與鎢合金扇形塊的干涉配合，在額定轉速和設計轉速下，厚壁的外輪轂提供了重金屬合金扇形塊的保持力.因此，該鎢合金始終處于受壓狀態，而避免鎢合金材料受到拉伸載荷.飛輪裝配模型如圖1所示.

圖1 飛輪裝配模型Fig.1 Assembly model of flywheel

1.2 飛輪完整性分析要求

主泵飛輪外徑為950mm、內徑為307mm、厚度為408mm，飛輪的額定轉速為1 800r／min，設計轉速為2 250r／min.飛輪完整性分析包括強度分析和斷裂力學分析.強度分析包括在額定轉速下，飛輪的一次應力小于1／3屈服應力；設計轉速下，飛輪的一次應力小于2／3屈服應力；斷裂力學分析為飛輪在有最大假想裂紋的工況下，判斷裂紋處的應力強度因子是否小于臨界應力強度因子.

2 解析設計

2.1 軸對稱模型

解析法沿軸橫截面建立軸對稱模型.求解過程中假設：將鎢合金扇形塊簡化成一個圓環，即不考慮合金扇形塊之間的相互作用.對實心內輪轂、鎢合金以及外輪轂均按平面應力處理.軸對稱模型見圖2，圖中P1，P2為A，B面徑向應力；A，B位置為內輪轂與鎢合金以及鎢合金與外輪轂接觸位置；r1，r2為飛輪內輪轂內外徑；r3，r4為鎢合金和飛輪外輪轂外徑.

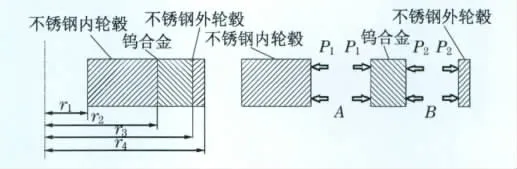
圖2 飛輪平面模型Fig.2 Plane model of flywheel

飛輪內輪轂以及外輪轂材料參數取彈性模量E1＝E3＝1.93×1011Pa，密度ρ1＝ρ3＝7 850kg／m3，泊松比υ1＝υ3＝0.3；鎢合金材料參數取彈性模量E2＝3.25×1011Pa，密度ρ2＝17 500kg／m3，泊松比υ2＝0.3.

2.2 額定轉速及設計轉速下應力計算

外輪轂與鎢合金扇形塊為過盈配合.在初始狀態下，外輪轂內徑小，鎢合金外徑大，兩者相差過盈量δ.由于過盈配合產生的壓力，外輪轂與鎢合金均受壓.當飛輪旋轉時，在離心力的作用下，外輪轂與鎢合金均向外擴張，由于外輪轂向外擴張位移大于鎢合金的擴張位移，兩環面之間的過盈量縮小為δ’.

飛輪在額定轉速下，先計算出殘余過盈量δ’.在離心力的作用下，鎢合金外表面徑向位移［2］為

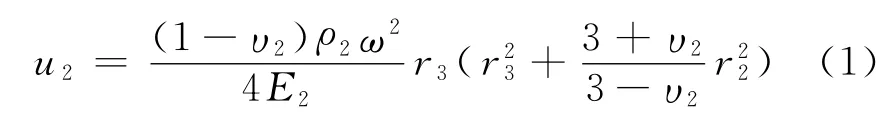
式中，ω為角速度.

外輪轂的內表面徑向位移為

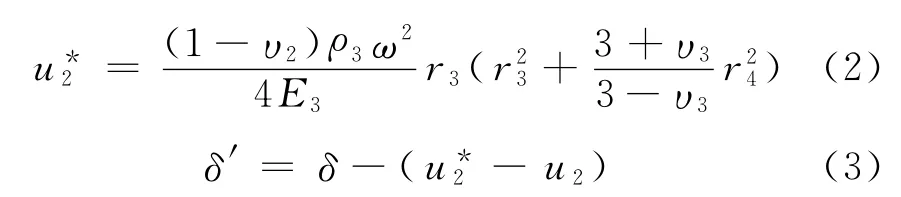
根據內輪轂的位移和應力關系［3］建立方程

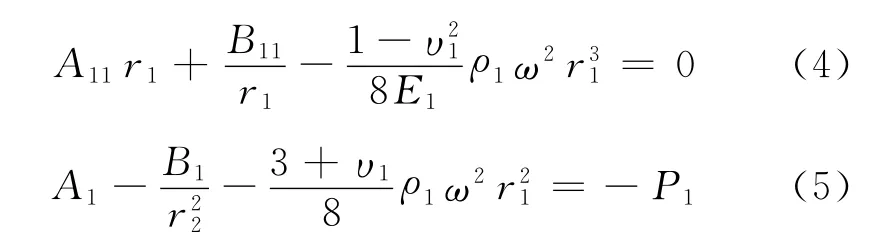
根據鎢合金的應力關系建立方程

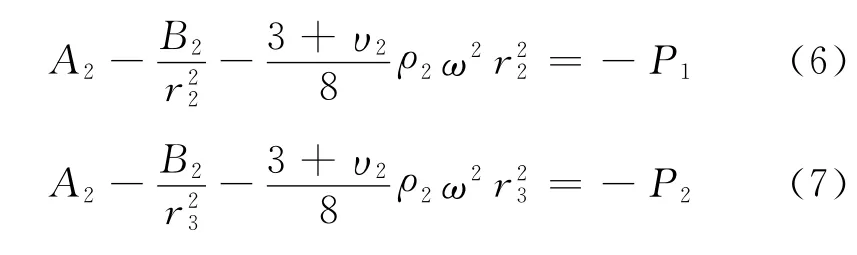
根據外輪轂的應力關系建立方程

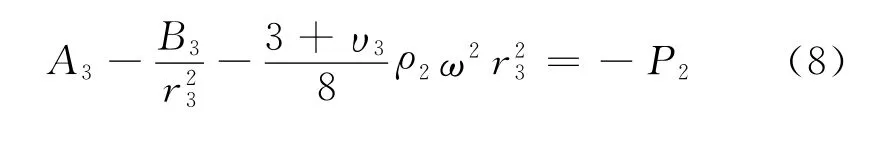
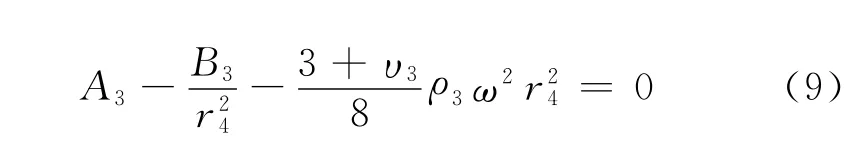
根據內輪轂與鎢合金及鎢合金與外輪轂接觸面位移關系建立方程

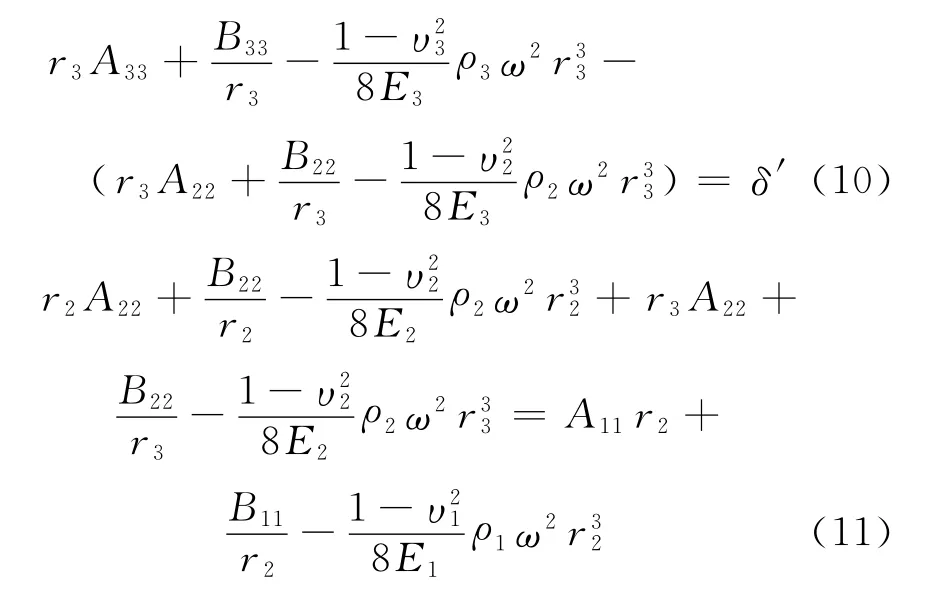
式（4）～式（11）中，Ai，Bi，Aii，Bii為計算系數，i＝1，2，3.將上文中相關參數帶入式（1）～式（11），得出額定轉速以及設計轉速下A，B位置應力以及位移如表1所示.

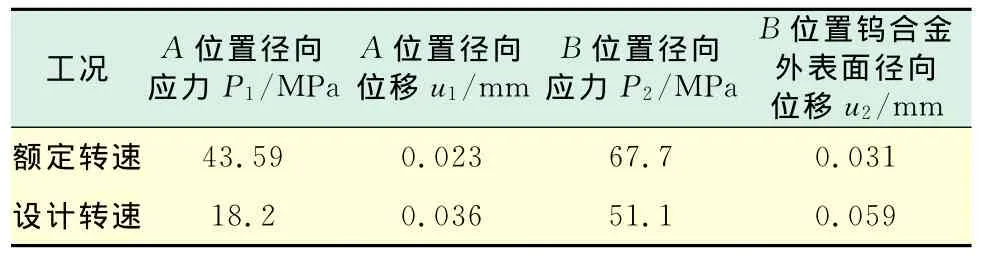
表1 額定轉速及設計轉速下A和B位置應力及位移結果Tab.1 Stress and displacement results in position A and Bunder rated and design speed

3 有限元分析

3.1 分析模型

采用ANSYS軟件進行分析.采用八節點六面體單元，共34 386個節點，38 336個單元.有限元模型示如圖3所示.為了準確分析飛輪在旋轉和過盈條件下的應力狀態，外輪轂與鎢合金之間按非線性接觸處理.在飛輪的軸向中間平面做對稱約束，實心內輪轂的內表面做徑向位移約束.這是考慮了飛輪軸向中間平面不發生軸向位移，因此在飛輪的軸向中間平面做對稱約束.

3.2 結果分析

3.2.1 強度分析

飛輪在額定轉速和設計轉速下的徑向應力和位移分布如圖4和圖5所示.

由圖4和圖5得出，在額定轉速下，A位置徑向應力約為43.57MPa，徑向位移約0.021mm，B位置徑向應力約為65.1MPa，鎢合金外表面徑向位移約0.03mm，飛輪的最大一次應力為78.7MPa；在設計轉速下，A位置徑向應力約為22.7MPa，徑向位移約0.039mm，B位置徑向應力約為52.45MPa，鎢合金外表面徑向位移約0.057mm，飛輪的最大一次應力為89.8MPa.將上述結果與應力限值進行比較，不考慮峰值應力，具體結果見表2.

圖3 飛輪有限元模型Fig.3 Finite element model of flywheel

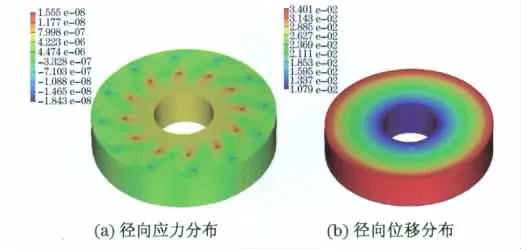
圖4 額定轉速下飛輪徑向應力分布與位移分布Fig.4 Radial stress and displacement distribution of flywheel in rated speed

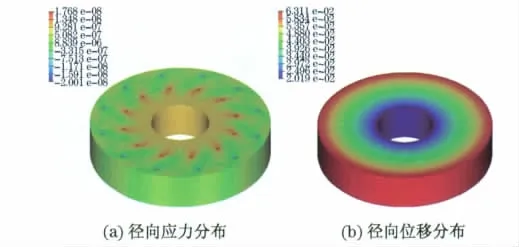
圖5 設計轉速下飛輪徑向應力分布與位移分布Fig.5 Radial stress and displacement distribution of flywheel in design speed

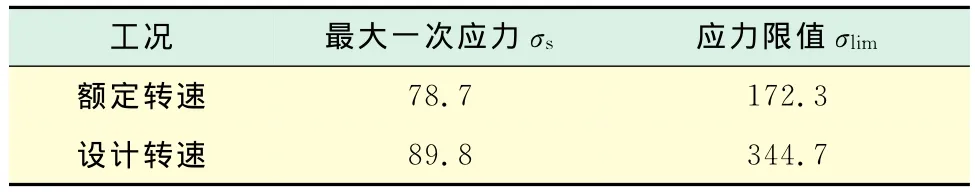
表2 飛輪應力計算值Tab.2 Calculated stresses of the flywheel MPa

從表2可知，飛輪在額定轉速和設計轉速下的應力強度滿足應力限值.

3.2.2 斷裂力學分析

按照斷裂力學原理，首先假定在飛輪最危險部位存在一最大裂紋，并計算該部位I型應力強度因子KI，然后將KI值與臨界應力強度因子KIC相比較，判斷是否能防止延性斷裂.

根據ASME附錄G－2120，最大假想裂紋方向垂直于最大應力方向.設初始裂紋尺寸如下：裂紋深度Wd為飛輪截面寬度的1／4，即Wd＝（D－a）／4＝（950－307）／8＝80.375mm；裂紋長度應為飛輪厚度的1.5倍，即482.25mm，而飛輪厚度只有408mm，則裂紋長度取408mm（貫穿飛輪厚度）.

進行斷裂力學評價時，將一次應力和二次應力分為薄膜應力和彎曲應力.薄膜應力和彎曲應力的計算公式［7－8］為

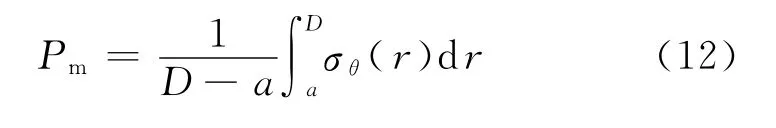
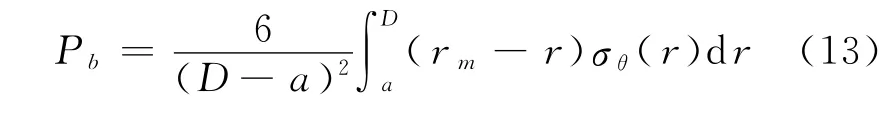
式中，a，D為飛輪內外半徑；r為半徑；平均半徑rm＝（a＋D）／2；σθ（r）為環向應力.

按照ASME附錄圖G－2241－1來選取額定轉速及設計轉速下的彎曲應力系數Mb和薄膜應力系數Mm.額定轉速與設計轉速下的分析結果列于表3.其中臨界應力強度因子KIC＝148MPa·m1／2；Mb＝2／3Mm，KIp＝2KIm＋2KIb，KI＝KIp＋KIs；KIm為薄膜拉伸應力強度因子，KIb為彎曲應力強度因子，KIp為一次應力引起的應力強度因子，KIs為二次應力引起的應力強度因子.

從表3可知，額定轉速與設計轉速下的總應力強度因子KI＜KIC，因此飛輪應力強度因子滿足要求，即在額定轉速和設計轉速下不會出現延性斷裂，能夠滿足結構的完整性要求.

表3 應力強度因子計算Tab.3 Calculated values of stress intensity factor

4 解析解與有限元結果對比

解析法計算出的A位置和B位置徑向應力和位移結果以及有限元分析得出的A位置和B位置應力和位移結果見表4，由表4可見，解析法與有限元方法的結果相近，解析分析所進行的假設合理，分析結果可信.

表4 解析解與有限元結果對比Tsb.4 Conparison between analytical solution and finite element results

5 結 論

a.飛輪在額定轉速以及設計轉速下最大一次應力分別為78.7MPa和89.8MPa，均小于應力限值，滿足強度要求.

b.額定轉速應力強度因子為91.9MPa·m1／2，設計轉速下應力強度因子為105.8MPa·m1／2，均小于臨界應力強度因子148MPa·m1／2，飛輪不會出現延性斷裂.

c.從解析解與有限元結果的對比可以看出，在兩個接觸A，B位置的徑向應力和位移值結果相近，可以證明解析分析所進行的簡化和假設合理，并且證明有限元分析的結果可信.

［1］李夢啟.三代核電反應堆冷卻劑泵屏蔽電機的技術特點［J］.大電機技術，2009，8（10）：1－4.

［2］楊鼎寧，鄒經湘.儲能飛輪過盈／脫落過程研究［J］.機械工程學報，2003，39（4）：1－7.

［3］黃載生，周士森彈性力學與應用［M］.杭州：浙江大學出版社，1995.

［4］Park J S，Song H C，Yoon K S，et al.A structural integrity evaluation for the interference－fit flywheel of reactor coolant pump［C］∥ ASME／JSME 2004 Pressure Vessels and Piping Conference，San Diego，2004.

［5］付月，張建宇.基于ANSYS的復合材料飛輪三維有限元分析［J］.高性能復合材料結構制造技術，2007，33（1）：63－69.

［6］張貴濱.冷卻劑泵電機飛輪完整性分析［J］.民營科技，2010（6）：16.

［7］張強，李昊.柴油機飛輪的應力分析［J］.農業機械學報，2002，33（4）：1－5.

［8］李笑天，鞠紅惠.主循環泵慣性飛輪完整性分析［J］.原子能科學技術，2007，41（4）：1－6.