雙重符合性審計抽樣時的抽樣規模的確定

耿修林

0 引言

運用抽樣方法開展審計活動已有近百年的歷史，經過這么多年的發展產生了許多樣本審計測試的組織方式，它們大體上可區分為兩大類別，即概率抽樣和非概率抽樣。非概率性質的審計抽樣能充分融入審計的意圖和審計人員的從業經驗，但由此得到的樣本測試結果原則上只能反映問題是否存在，不便于對審計對象總體情況做出符合數理邏輯的推斷。純概率意義上的審計抽樣，雖然能保證由樣本測試上升到對審計對象總體的反映，但在審計目的不很明確、審計人員業務經驗不足時，一味依賴于隨機規則實施抽樣審計，有可能會產生較大的風險，甚至遺漏或不能找出問題所在[1]，這或許也是純概率審計抽樣測試在實際使用中時常遭受詬疑的原因之一。對此，如果采用試探性做法，先從審計對象總體中按概率方式抽取一個較大規模的樣本，在初步檢查掌握部分情況后再從這個較大規模的樣本中抽取較小水平的測試樣本，則可以彌補“直接抽樣”的不足。這樣的樣本抽取方式，習慣上稱之為雙重抽樣或雙相抽樣，其基本特征是從樣本中再抽取樣本[3]。

在相同的抽樣規模和樣本推斷信度下，分層審計抽樣的效果要好于簡單隨機審計抽樣[3][4]。但在審計人員經驗不足或不存在明顯的分層標志情形下，要想取得良好的分層審計抽樣估計效果也是不大有可能的。假如采用雙重審計抽樣，在獲得第一重審計樣本后，通過對第一重樣本的直觀觀察和判斷，然后再用分層抽樣的辦法，從第一重樣本中抽取較小規模的第二重樣本以此進行測試分析，就有可能會改善審計樣本估計效果。

符合性審計也叫合規性審計，它主要檢查審計對象總體錯誤發生的比例或被審計單位相關內控制度的執行情況等[2]。符合性審計中成數是其重要的估計內容，由于這種測試內容的特征，要是直接按照統計隨機原則抽取測試樣本可能在某些場合下行不通或者效果不好，原因是：符合性特征的發生帶有某種程度的“稀少性”，可能在大量的審計單元中都不存在，這時先抽取一個比較大的第一重樣本把那些真正具有審計測試意圖的單位挑選出來再實施抽樣，可能有助于快速確定出對測試具有價值的檢查樣本；通過雙重抽樣的第一重樣本檢查，能夠獲得有關輔助性資料，這對改善審計樣本尤其是分層估計效果會有實質性幫助；縱使第二重樣本單位檢查的信息不能獨立發揮作用，至少也可以對第一重樣本審計檢查的結果進行評估和調整[4]。

1 雙重符合性抽樣分層估計量的精度

為便于討論雙重符合性審計抽樣時的抽樣規模，在此先對雙重符合性抽樣分層估計原理進行簡要的說明。假定從審計對象總體中按照純隨機抽樣方法抽取容量為n′的第一重樣本，然后將其分成L層，其中第h層的第一重樣本單位數為 n′h(h=1,2,...,L)，n′=n′1+n′2+...+n′L。從第一重樣本中抽取容量為n的第二重樣本，屬于第二重樣本第h層的樣本單位數為nh，那么n=n1+n2+...+nL。用表示由第一重抽樣得到的第h層層權，總體的第h層真實層權用Wh=N′h(N′)-1表示，N′為總體全部單位數，N′h為總體第h層單位數目。Yhj為第h層第 j個總體單位測量，且取值0或者1，yhj表示第h層第 j個樣本單位測量，同為0-1變量。在這些符號的約定下，容易得到審計對象總體符合性成數P=WhPh的樣本估計量，因為第一重樣本的層成數 p′h為

第一重樣本成數p′

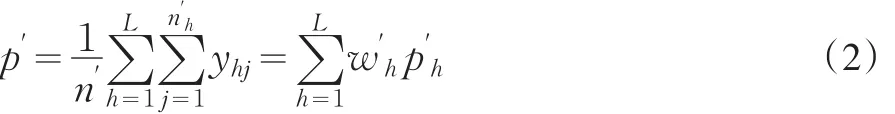
第二重樣本第h層的樣本成數

它可用作第一重樣本層成數 p′h的估計，并且還是無偏的估計量[4]。此時，總體符合性成數P的估計量可以構造成

其中，pstd表示雙重分層抽樣時的樣本符合性成數。

在抽樣測試水平比較大時，理論上可以說明pstd是總體均值P的無偏估計，用 pstd估計總體符合性成數P的方差為

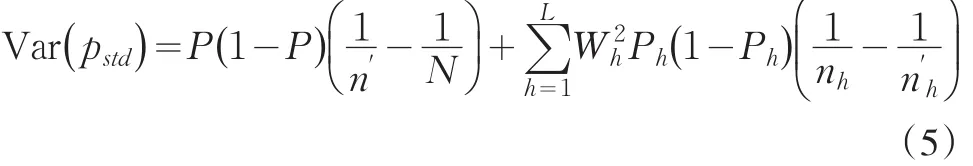
在第一重抽樣比和第二重抽樣比較小的情形下，式（5）可簡單表示成

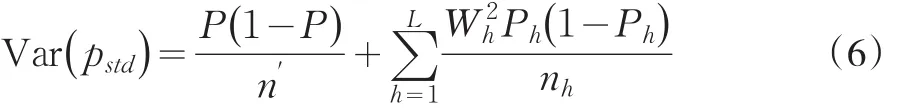
2 雙重符合性審計抽樣分層推斷時的抽樣規模

對雙重符合性審計抽樣測試問題，一方面需要給出第二重抽樣水平的計算辦法，另一方面也要確定出第一重抽樣測試的樣本檢查規模。依據決策分析的原理，大致有兩種處理方法，即“常規決策”分析和貝葉斯決策規則。

2.1 “常規決策”分析

樣本估計精度大小與樣本推斷風險之間存在一定的聯系，“常規決策”分析是根據事先給定的費用預算約束，盡可能地提高抽樣估計精度即最大限度地降低估計量的方差，然后以此來確定抽樣測試水平。

雙重抽樣測試的費用由兩部分組成，一部分是抽取第一重測試樣本發生的費用，另一部分是抽取第二重測試樣本的費用[3]。設第一重測試樣本每個單位的可變測試費用為c1，這樣第一重抽樣總的可變檢查費用c1n′。由于第二重樣本是符合性審計抽樣測試的關鍵部分，有關這一部分的檢查費用需要給出更為詳細的說明，假定第二重測試樣本中每個層的樣本單位檢查的可變費用為c2h，這樣為簡單起見分層用雙重審計抽樣測試的全部可變費用可采用如下的線性函數進行描述

其中的C表示測試檢查的全部可變費用支出。

根據一般的抽樣調查原理，由于第二重測試樣本每個層中分配的樣本單位數是隨機變量，為此需要考慮在固定第二重抽樣各層抽樣比的基礎上，計算審計樣本測試全部可變費用支出的數學期望

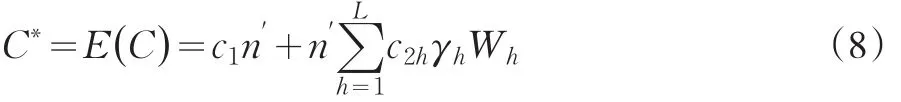
其中，γh為既定的第二重測試樣本的層抽樣比。

估計量 pstd的方差由式（5）給出，在引進第二重測試樣本固定的層抽樣比情況下，可以將式（5）改寫成

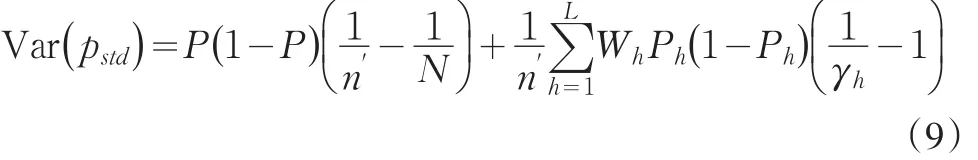
對其進行變形處理

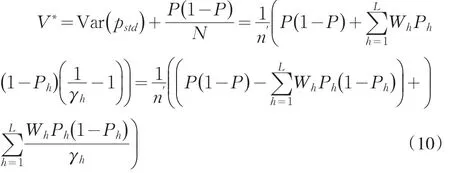
把式（8）與式（10）相乘得

根據CAUCHY-SCHWARZ不等式得

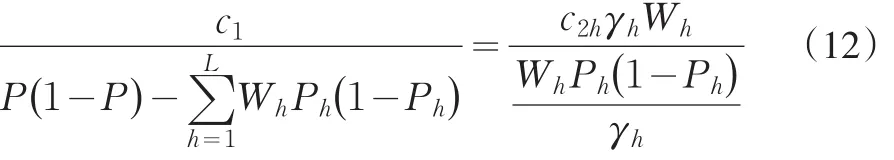
由此可解得第二重符合性審計抽樣中各層的抽樣比

把式（13）代入到式（7），得到第一重抽樣的最小抽樣測試水平，即

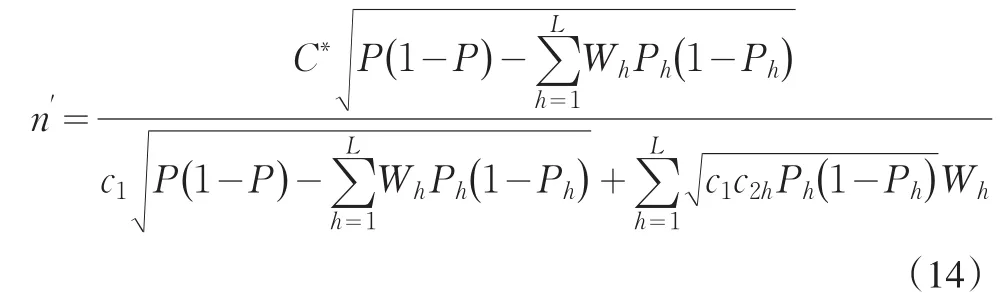
在第一重抽樣規模給定時，可以得到

如上所述，第二重樣本量是隨機變量，對其求數學期望可以給出雙重符合性測試抽樣時第二重抽樣的平均抽樣水平

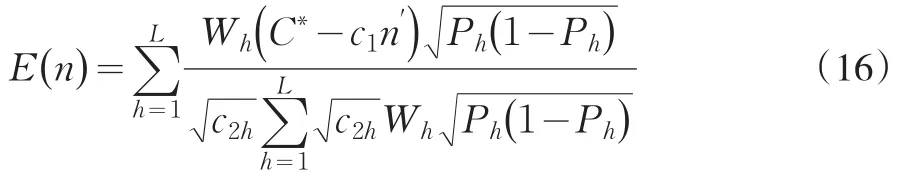
對雙重符合性測試抽樣在第二重抽樣時層間樣本量采用等比例分配，此時式（6）可簡潔表示成

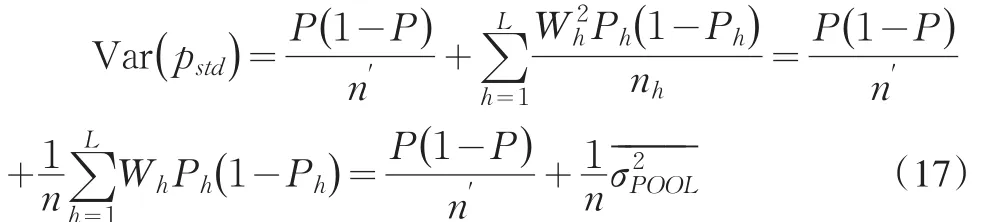
此時，假定檢查可變費用采用函數

1.2.1 實驗組教學方法 Mini-CEX考核評估項目包括7種：病史采集；體格檢查；醫德醫風；醫患交流；臨床診斷；治療方案；整體評價。實施步驟：（1）設計以Mini-CEX考核內容為基礎的內科護理學授課計劃及內容，并在教案中體現。（2）教師布置病例，要求護生結合病例進行角色扮演，內容包括病史采集、體格檢查、臨床診斷、治療方案，其間要體現醫德醫風、醫患交流。（3）每次課程最后20分鐘，教師抽取1名護生以Mini-CEX考核表格進行全面考核，當場進行評價并反饋。Mini-CEX的優點是護生可以及時獲得反饋，在給一名護生進行反饋的同時，其他護生也有收獲。

那么，關于雙重審計抽樣的抽樣規模確定，還可以有個稍微簡單一點的計算方法。

聯合式（17）和式（18），構造如下的符合性抽樣規模決策分析數學規劃模型

把約束規劃轉換成無約束問題，利用拉格朗日法則能得到

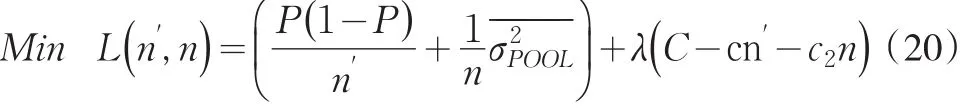
通過求極值，得到

對測試費用給定，把式（21）代入式（18）

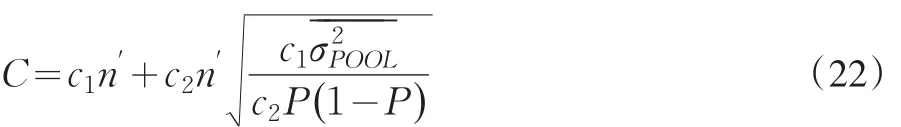
由此解出的第一重符合性抽樣測試規模的計算公式

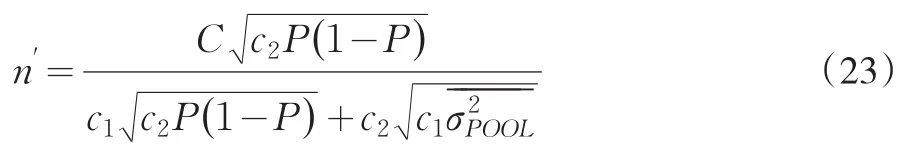
反過來，把式（23）代入到式（18），能得到第二重符合性抽樣測試水平的計算公式

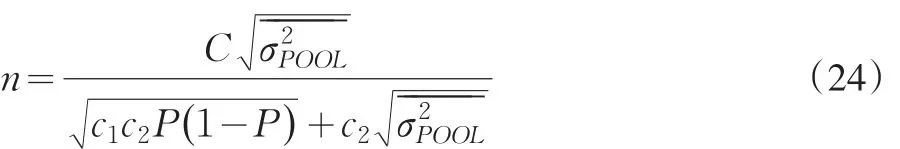
2.2 貝葉斯決策規則

運用“常規決策”分析法確定符合性審計抽樣測試水平的“缺陷”是，它直接把樣本估計精度和抽樣測試費用這兩類性質不同的東西放在一起處理，雖然最終能給出分析的結果，但從事理上有說不通的嫌疑。貝葉斯決策規則在確定符合性審計抽樣測試規模的時候，不僅把樣本估計精度與由此衍生出來的判斷失誤風險損失有機地結合起來，同時還兼顧了審計樣本測試發生的費用[5]。因此，貝葉斯決策規則對審計抽樣測試的損失或費用運用得更為深刻，也更符合客觀現實的邏輯。

假定由樣本測試資料做出審計判斷失誤的損失可以用價值量來刻畫；由樣本測試資料進行審計判斷的失誤可以用總體符合性成數估計的誤差來反映。那么，根據貝葉斯決策的基本做法，可以構造如下形式的雙重符合性審計抽樣規模確定模型：

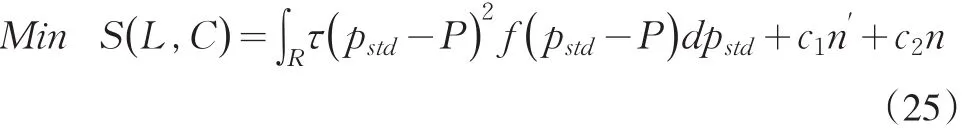
在第二重審計測試抽樣層間樣本數目采用等比例分配的假定下，式（25）等價于

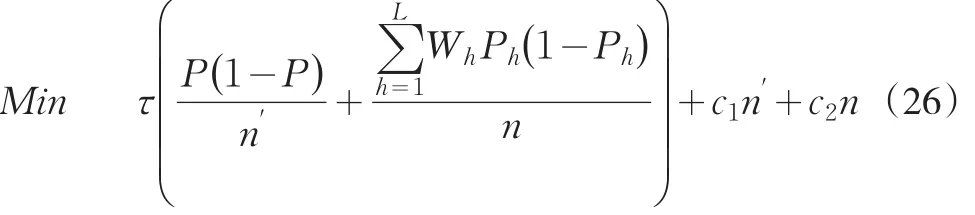
通過求解無條件極值可得到

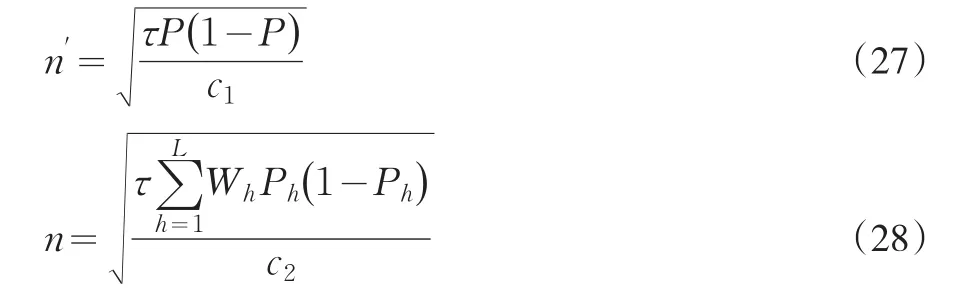
3 結論

樣本測試規模的大小對審計樣本測試推斷結果的影響是客觀存在的。按照概率統計的一般原理，樣本測試規模過小，有可能會產生更大的樣本估計風險；反過來樣本測試規模較大，由此會在一定程度上提高估計精度，相應地也就能降低樣本推斷風險。但測試樣本也不可能無限增大，否則就達不到抽樣審計的目的。另外，既然是抽樣審計樣本測試組織方式可以針對特定對象的特征進行安排，但樣本測試的規模需要結合樣本推斷要求以及測試費用約束來加以確定。這一方面是為了增加工作的規范性；另一方面是為了減小審計責任和風險。

[1]李鳳鳴.審計學原理（第5版）[M].上海:復旦大學出版社,2011.

[2]毛節飛.審計理論與實務[M].北京:經濟科學出版社,2009.

[3]馮士雍,倪加勛,鄒國華.抽樣調查理論與方法[M].北京:中國統計出版社,1998.

[4][美]W.G.科克倫.抽樣技術[M].張堯庭,吳輝譯.北京:中國統計出版社,1985.

[5]Hans Peter Stuger.Asymmetric Loss Functionsand Sample Size Deter?mination:A Bayesian Approach[J].Austrlan Journal of Statistics,2006,(35).