4象限H橋功率單元PWM整流器的比例－積分－諧振控制

，

（1.北京交通大學 電氣工程學院，北京 100044；2.清華大學 電機工程與應用電子技術系，北京 100084）

1 引言

H橋級聯型多電平變換器具有模塊化的結構，易于制造，且控制方式簡單，無直流母線電容均壓問題，因此在中壓大容量電機調速領域獲得了廣泛應用［1－2］。

在一些工業應用領域，電機需要頻繁的啟動制動。在這種情況下，將電機制動的能量回饋至電網，對于實現節能環保有重要意義。如果H橋級聯型變換器每個功率單元都使用PWM整流器，實現能量雙向流動，整個H橋級聯型變換器就能夠實現4象限運行［3－4］。

使用PWM整流器可以控制直流母線電壓，因此直流母線電容容量通常比使用二極管不控整流的變換器的電容小很多。每個功率單元都減少直流母線電容容量，使得整個H橋級聯型多電平變換器節省大量電容器，這對于降低變換器成本、提高可靠性很有意義。對于每個功率單元而言，H橋逆變器的輸出功率包含了2倍于輸出電壓頻率的分量，但是通常的PWM整流器控制策略主要針對直流分量［5－6］，這些2倍輸出電壓頻率的功率會引起直流母線電壓波動。為了抑制直流母線電壓波動，文獻［3］根據功率單元輸入輸出功率的平衡關系，為PWM整流器增加了負載功率前饋作為電流環的設定值，以期減小母線電容容量，但是由于使用PI調節器的電流環帶寬有限，電流并不能很好地跟蹤設定值，致使母線電壓波動仍然較大。另外，負載功率前饋方法需要將H橋逆變器交流側的占空比、瞬時電流等信息傳送給PWM整流器，系統設計較為復雜。

本文采用比例－積分－諧振（PIR）調節器［7］對PWM整流器進行控制，電壓、電流控制性能良好；只需知道逆變器的輸出頻率，系統設計就可以得到簡化。在功率單元原型系統上的實驗驗證了該方法的有效性。

2 4象限H橋功率單元運行分析

4象限H橋級聯型變換器的結構如圖1所示，逆變器的每一相輸出都是由多個功率單元的輸出串聯而成，串聯的功率單元數由負載電壓等級決定。每個功率單元的結構完全相同，其主電路如圖2所示，它與傳統的功率單元的區別在于使用了PWM整流器而不是二極管整流器，因此它可以實現對母線電壓的控制，還可以使能量雙向流動。

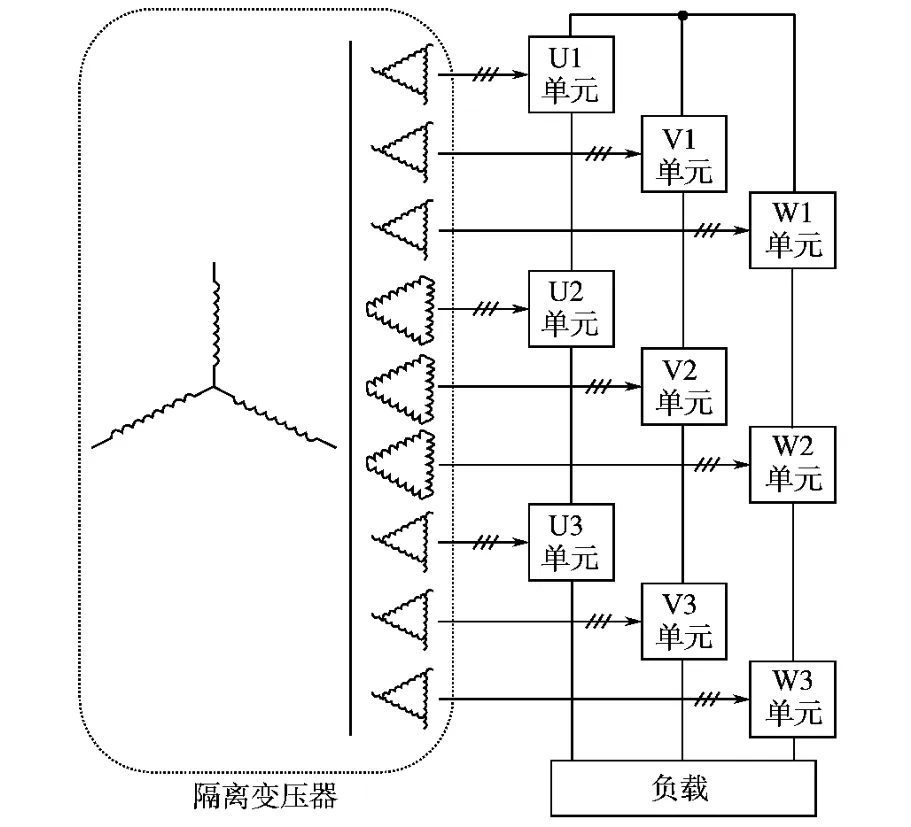
圖1 4象限H橋級聯型多電平變換器Fig.1 Four－quadrant cascaded H－bridge multilevel converter

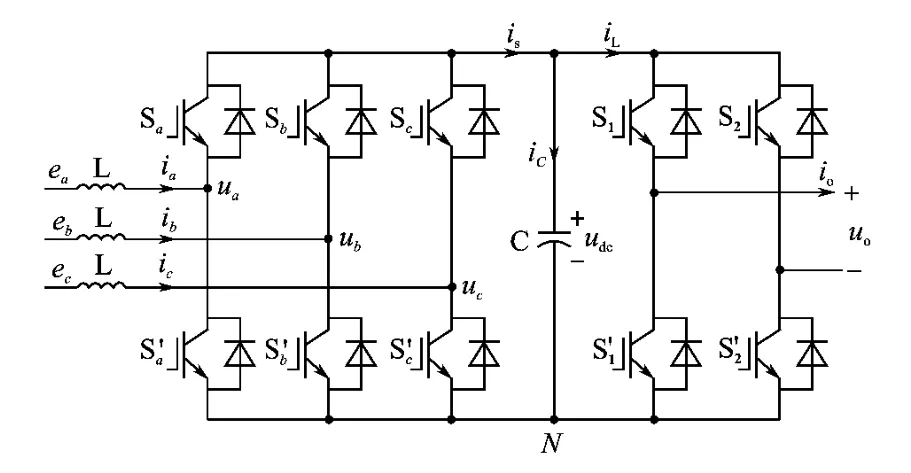
圖2 功率單元主電路Fig.2 Main circuit of a power cell

每個單元的輸入側PWM整流器相對比較獨立，可以分別獨立控制，控制目標是給H橋逆變器提供穩定的直流電壓。具體控制方式可以采用電網電壓定向控制［5］或者直接功率控制［6］等方式。本文基于電網電壓定向控制策略。

電網同步旋轉坐標系下，如果忽略交流電抗器的電阻，并假定開關器件為理想開關，PWM整流器交流側電壓方程為

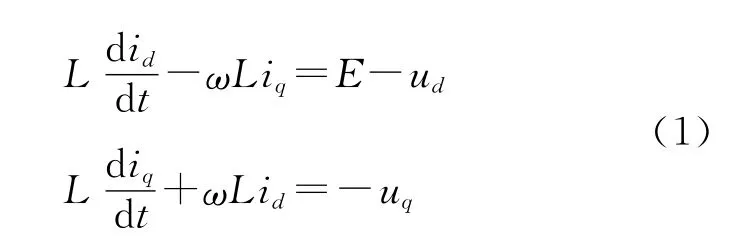
式中：E是PWM整流器輸入側電壓矢量的幅值。進一步假定電抗器儲能變化可以忽略，可以得出整流器的功率平衡關系如下

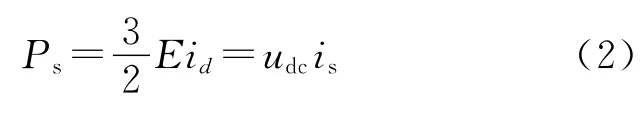
由式（2）可知，輸入整流器直流側的功率只與d軸電流有關，而與q軸電流無關。

如果采用傳統的電網電壓定向控制方法，在同步旋轉坐標系下對PWM整流器進行雙閉環控制，那么外環的直流母線電壓控制器和內環的交流電流控制器都可以是比例－積分（PI）調節器。對于直流負載或者三相逆變對稱交流負載，這種控制策略具有很好的效果。但是在H橋功率單元中，由于H橋逆變器的輸出功率含有2倍于輸出電壓頻率的交流分量，如果仍然采用PI調節器進行控制，那么直流母線電壓會有很大幅度的脈動。下面對此進行詳細分析。

在分析控制策略時，通常假定變換器的效率很高，損耗可以忽略。在此假設下，H橋逆變器交流側和直流側的功率平衡關系式為

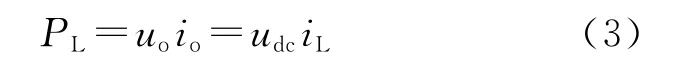
考慮到控制器設計主要關注受控對象的低頻特性，一般假設電壓電流高次諧波可以忽略。此時逆變器輸出的電壓和電流可以用平均模型分別表示為

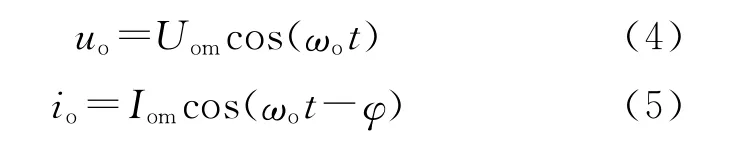
式中：Uom，Iom分別為輸出電壓和電流的幅值；ωo為輸出的角頻率；φ為負載的功率因數角。

要保持H橋功率單元的直流母線電壓恒定，必須使Ps＝PL，即PWM整流器的輸入功率與H橋逆變器的輸出功率相等，由式（2）和式（3）得到

將式（4）和式（5）代入式（6），得到

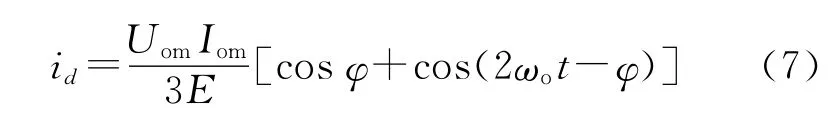
式（6）和式（7）反映了理想情況下的d軸電流瞬時值。由式（7）可以看出，由于逆變器是由H橋構成的，它的輸出功率除了直流分量外，還含有2倍于輸出電壓頻率ωo的交流分量，因此整流器d軸電流也必須包含直流分量和2ωo頻率分量，才能穩定住直流母線電壓。

傳統電網電壓定向控制策略的PI調節器可以對直流分量有很好的控制性能，但是對于2ωo頻率交流分量總是存在靜差。這就使得PWM整流器不能提供與H橋逆變器相平衡的瞬時功率，總會有2ωo頻率的功率交流分量流入直流母線，造成直流母線電壓的脈動。

3 PWM整流器的PIR控制策略

為了解決對于2ωo頻率交流分量的跟蹤問題，引入諧振（Resonant）調節器，并將諧振頻率設置為2ωo。與傳統的PI調節器結合，構成PIR調節器，它的傳遞函數是

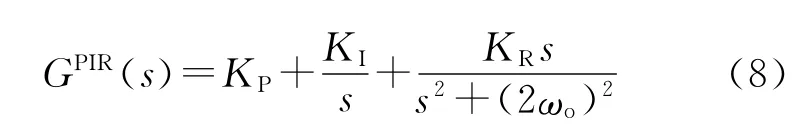
式中：KP，KI，KR分別是比例、積分和諧振調節器。

在諧振頻率2ωo處，控制器的開環幅頻特性趨于無窮大，因此閉環系統對于頻率為2ωo的指令值可以實現無靜差跟蹤。以電流環為例，使用PIR調節器和PI調節器的電流環閉環頻率特性對比如圖3所示。

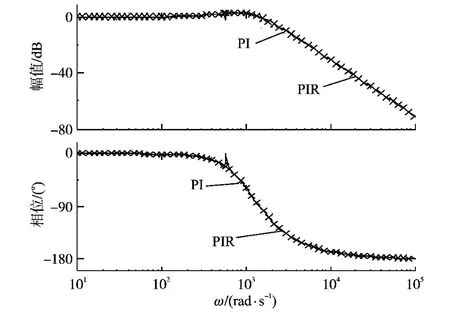
圖3 電流環閉環頻率特性Fig.3 Closed－loop frequency characteristic of current loop

從圖3中可以看出，PIR調節器控制的電流環在諧振頻率2ωo處的閉環增益為1。此外，諧振調節器只對諧振頻率附近極小頻段內的頻率響應特性有較大影響，其余頻率范圍的頻率響應主要由PI調節器決定。

采用PIR調節器對PWM整流器的電壓環和流環進行控制，控制策略如圖4所示。

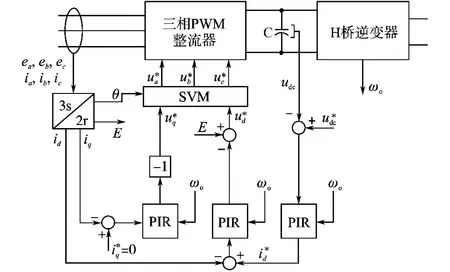
圖4 改進的PWM整流器控制策略Fig.4 Improved control strategy for PWM rectifier

由于直流母線電壓指令值為直流量，即2ωo頻率分量為零，使用PIR調節器對直流母線電壓進行控制，可以對2ωo頻率分量進行無靜差跟蹤，也就是能夠消除2ωo頻率分量。

根據前面的分析，消除直流母線電壓的2ω。頻率脈動需要使d軸電流包含該頻率分量，因此，外環電壓控制器的輸出（即內環d軸電流指令值）中必然也含有2ωo頻率分量。電流環也需要使用PIR調節器，使d軸電流能夠無靜差的跟蹤指令值。

相比于文獻［3］中的負載功率前饋控制策略，使用本文的方法，PWM整流器的控制無需知道H橋逆變器交流側的占空比、瞬時電流等信息，僅需要H橋逆變器的輸出頻率即可，減小了通信量和傳感器的安裝數量。

4 實驗結果

在一個4象限H橋功率單元原型系統上對上述控制策略進行了實驗驗證。功率單元的整流橋和逆變橋都使用三菱公司的PM50RVA120型IPM，其中逆變橋只使用了IPM 3個橋臂中的2個構成H橋，剩下的1個橋臂完全關斷。控制器為TI公司的TMS320F2812型DSP，工作頻率為150MHz。實驗系統的其他參數為：PWM整流器，電網線電壓380V，交流電抗值5.1mH，開關頻率2kHz；直流母線電容值110μF，電壓設定值620V；H橋逆變器，調制波頻率45Hz，開關頻率2kHz；負載電感20mH，電阻45Ω。

圖5所示為4象限H橋功率單元的實驗波形，從上到下依次是：H橋逆變器輸出電流，直流母線電壓，PWM整流器d軸電流指令值，d軸電流實際值，d軸電流誤差。在0.2s之前，PWM整流器采用PI調節器控制，在0.2s時投入諧振調節器，即PIR調節器控制。

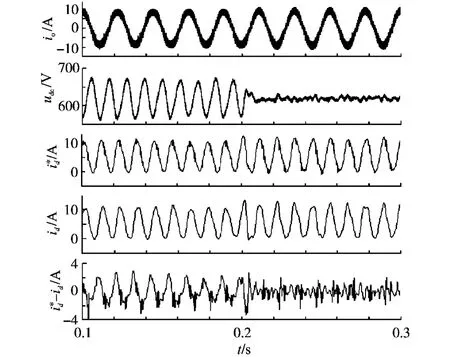
圖5 0.2s時投入諧振調節器的實驗波形Fig.5 Experimental waveforms of turning on resonant regulator at 0.2s

從實驗波形可以看到，由于H橋逆變器輸出基波頻率為45Hz，采用PI調節器控制時，直流母線電壓含有90Hz的交流分量，波動峰峰值約為120V；PWM整流器d軸電流指令值也包含90Hz分量，雖然PI調節器使d軸電流實際值也包含90Hz分量，但是d軸電流誤差值仍然包含90Hz分量，說明d軸電流實際值并沒有很好地跟蹤指令值。

在投入諧振調節器后，PWM整流器處于PIR調節器的控制下，在不到0.01s的時間內，直流母線的90Hz脈動迅速得以抑制，電壓波動明顯減小；且d軸電流誤差值中也不再含有90Hz分量；暫態過程非常迅速且無沖擊。由于直流母線電壓質量變好，H橋逆變器的輸出電流波形也更加接近正弦。實驗結果說明了PIR調節器對于H橋功率單元的PWM整流器具有很好的控制效果。

5 結論

在4象限H橋級聯型多電平變換器中，H橋功率單元的輸入環節為三相PWM整流器，輸出環節為單相H橋逆變器。本文根據單相H橋負載的特點，應用PIR調節器作為前端PWM整流器的電壓環和電流環的控制器，抑制了直流母線電壓的2倍輸出頻率脈動。實驗結果表明，即使直流母線電容很小，上述控制策略也能使直流母線電壓平穩，具有良好的控制性能。

［1］Hammond P W.A New Approach to Enhance Power Quality for Medium Voltage AC Drives［J］.IEEE Trans.Ind.Appl.，1997，33（1）：202－208.

［2］李永東，饒建業.大容量多電平變換器拓撲－現狀與進展［J］.電氣技術，2008（09）：7－12.

［3］Perez M A，Espinoza J R，Rodriguez J R，etal.Regenerative Medium－voltage AC Drive Based on a Multicell Arrangement with Reduced Energy Storage Requirements［J］.IEEE Trans.Ind.Electron.，2005，52（1）：171－180.

［4］吳鳳江，趙克，孫力，等.一種新型四象限級聯型多電平逆變器拓撲［J］.電工技術學報，2008，23（4）：81－86.

［5］Blasko V，Kaura V.A New Mathematical Model and Control of a Three－phase AC－DC Voltage Source Converter［J］.IEEE Transactions on Power Electronics，1997，12（1）：116－123.

［6］王久和，李華德，李正熙.電壓型PWM整流器直接功率控制技術［J］.電工電能新技術，2004，23（3）：64－67.

［7］Zmood D N，Holmes D G.Stationary Frame Current Regulation of PWM Inverters with Zero Steady－state Error［J］.IEEE Trans.Power Electron.，2003，18（3）：814－822.