人體站姿豎向振動等效單自由度模型參數研究

楊 予，楊云芳，洪 震，胡杰云，蔡其茅

(浙江理工大學 建工學院 土木系，杭州 310018)

由于現代工程材料和技術的發展，現代都市中的建筑結構有輕量化發展趨勢，近年來建筑物中的人與結構耦合振動問題日益突出。在進行人與結構耦合振動分析時，常遇到的關鍵性問題是對人體進行合理的簡化建模并給出適當的模型參數。

在人體動力學建模方面，目前已經積累有許多研究成果，代表性的研究者有 Subashi[1]，Matsumoto[2－3]，Wei[4]，Griffin[5]等，常見研究方法是視人體為多自由度模型，采用裝有傳感器的剛性電液伺服振動臺，通過施加隨機振動激勵的方式測出不同頻段人體站姿或坐姿情況下與結構的接觸力或位移，然后根據實驗數據識別各人體模型的各部分參數。另一方面，考慮到分析相對便捷，人體單自由度簡化動力學模型在實際工程中仍有相當廣泛的應用，但從一些公開發表的文獻資料中不難發現，目前在模型參數取值上尚無統一標準，例如:何浩祥等在文獻[6]中采用的人體豎向自振頻率為3.84 Hz，Dougill在文獻[7]中采用了 2.3 Hz的人體豎向自振頻率和25%的阻尼比，陳建英等在文獻[8]中給出的人體豎向自振頻率為5.12 Hz，阻尼比為0.42，樊健生等在文獻[9]中采用的人體豎向自振頻率為 5.24，阻尼比為 0.39。

考慮到單自由度簡化模型參數取值對動力學分析結果的影響，很有必要對其進行更為深入的研究和探討。本研究的目的是通過理論推導和實驗測試手段得出人與結構作耦合自由振動時的等效單自由度簡化模型參數，并討論這些參數對結構參數和人體局部姿態的敏感性，為工程中的相關分析提供直觀的取值依據。

1 人體一維簡化理論

設當采用n(n＞1)自由度模型對人體進行描述時，人體與結構耦合振動的動力學特征可以滿足所需精度要求，則此時對應的人體一維簡化模型應為該多自由度模型的某一最佳數值逼近。為說明其原理，試考察圖1中所示的兩個耦合振動結構體系:

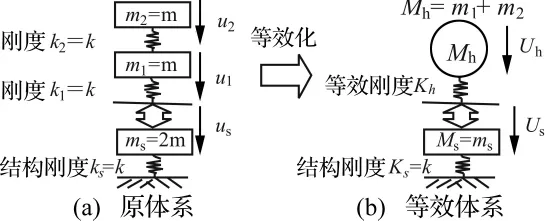
圖1 等效振動體系分析Fig.1 Theory of equivalent vibration system

圖1 (a)中一個兩自由度串聯彈簧－質量塊系統(代表人體)放置于一單自由度彈簧－質量塊系統上，構成耦合振動體系，設ks=k1=k2=k，ms=2m，m1=m2=m，如圖1(a)所示。由結構動力學可知該系統的主振型與各子系統的彈簧剛度與質量取值有關，若設該體系的初始狀態為{u0}=[1 1 1]T，{}=[0 00]T，則按振型分解法可求出質量ms的自由振動如式(1)所示:

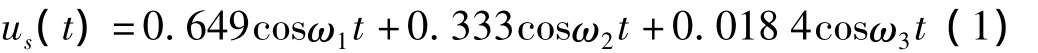
現考慮將該兩自由度串聯彈簧－質量塊體系等效化為單自由度模型，為便于工程應用，取新體系中的參數 Ks=k，Ms=ms，Mh=m1+m2，如圖 1(b)所示，則等效化問題可歸結為:求出新體系下的彈簧剛度Kh，使得相同初始條件下Ms的振動反應與原系統中ms的振動反應具有最佳近似性。

相應地，假定該系統初始狀態為{U0}=[1 1]T，，則按振型分解法可求出質量 Ms的自由振動，如式(2)所示:

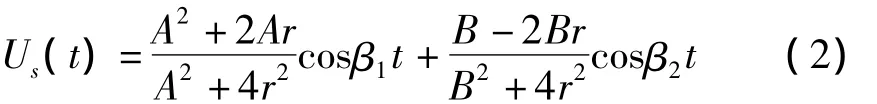
比較(1)、(2)兩式右端可見，想要上述兩個體系在任意t時刻的振動完全一致就必須讓各項系數和頻率值分別相等，而這顯然是不可能的。因此，為使一維等效簡化模型具有工程應用價值，可考慮按最小二乘法進行擬合，即作兩者誤差之平方對時間的積分函數F，如式(3)所示:

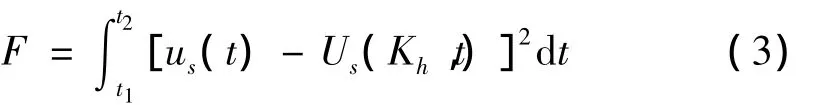
顯然，若能夠找到一個Kh值使得誤差函數F在所需特定積分時間段T=t2－t1內取極小值，則此Kh值就是該時間段內所求的一維等效模型的最佳逼近參數。

推及一般情形，在考慮阻尼的作用時，式(3)可改為:

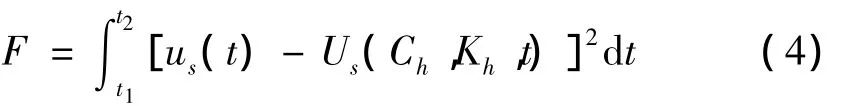
由此可見，本文中人體一維簡化模型的具體物理意義為:尋找適當的人體剛度值 Kh和阻尼值Ch使得簡化耦合振動體系結構振動反應與精確耦合振動體系結構振動反應的誤差在某所需特定時間段T內最小。

此外，根據上述分析尚可有如下推論:當結構取不同動力學參數時，由于耦合振動體系的主振型將發生相應變化，人體的一維簡化模型參數也隨之改變。

2 實驗測試與數據處理

根據上述等效原理，考慮到人體建模的復雜性，直接根據實驗數據導出一維等效參數較合理。為便于對比驗證，本文研究中利用兩臺不同原理的單自由度實驗臺進行測試，如圖2所示，并采用Power1401數采系統和壓電式加速度傳感器等對實驗臺進行加速度數據采集，采樣率為1 024 Hz。表1中列出了振動臺和待測志愿者的參數，其中振動臺一用于模擬自振頻率較高、質量較輕的剛性結構，振動臺二用于模擬自振頻率較低、質量較重的柔性結構。

圖2 實驗采用的兩種單自由度振動臺Fig.2 Two SDOF test rig used in experimental study

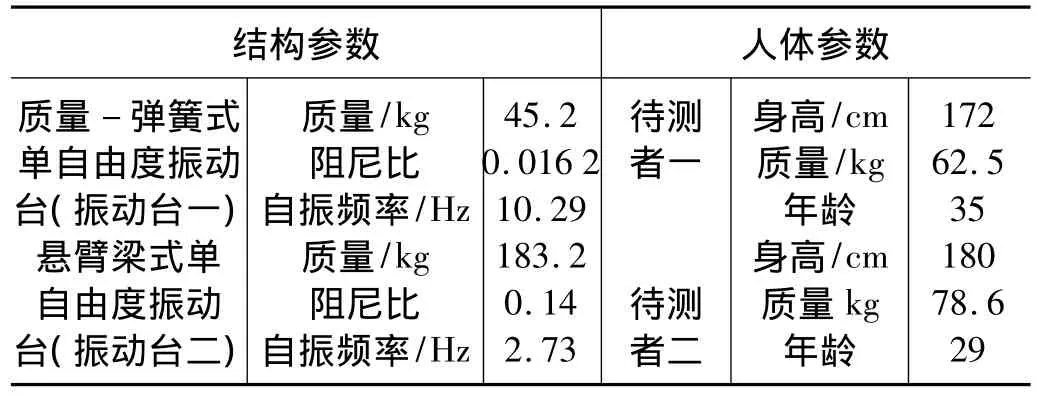
表1 人與結構耦合振動實驗參數條件Tab.1 Parameters of human body and test rigs

在實驗中采用賦予振動臺一定位移的方法進行初始激勵，為驗證參數對人體局部姿態的敏感性，分別測試了雙腳并攏自然直立、雙腳尖踮起直立、雙手向上直舉、雙腳尖踮起直立同時雙手向上直舉以及屈膝站立五種典型站立姿勢情況下的振動臺自由振動情況。

為避免出現不合理的結果，根據參考文獻[1－4]中的人體特征參數識別情況，在擬合分析中取人體豎向自振頻率和阻尼比的上下限值分別為0.1 Hz≤fh≤10 Hz，0≤ξh≤0.4，具體數據處理流程如下:

(1)取數據點P0，在P0處對采樣數據加矩形窗截取激勵完成后T=2 s時間段內的加速度向量[]，并對[進行規格化處理得到最大加速度為1的加速度向量[];(2)根據經驗給定合理的迭代初始頻率 fh0和初始阻尼 ξh0，將其與 Mh以及振動臺振動參數代入式(5)，并令時間步長為1/N，采用數值積分方法對自由振動進行求解，得出各時間點加速度向量[];

(5)考慮到截取測試數據的偶然性，調整截斷點P0位置作一維搜索，并重復步驟(1)－(4)，直至找到最小的二乘法誤差函數值，則此時對應的即為所求的人體單自由度等效自振頻率和阻尼比。

3 實驗結果分析

圖3(a)為剛性振動臺一所測得的加速度時程曲線以及參數擬合曲線，作為對比，圖3(b)中繪出了不考慮人體頻率和阻尼，將人體視為單純質量直接與實驗臺質量疊加作為單自由度振動體系的理論分析結果。由圖3可見，按本文方法得出的人體單自由度簡化模型與實驗結果具有不錯的擬合精度，在工程實用性上顯然好于將人體單純視為質量。

圖4給出了剛性振動臺一上五種典型站姿的等效參數分析結果(多次測試取平均值)，由圖可知:① 剛性振動臺上測試者的等效自振頻率受站姿變化影響的相對幅度較小，而等效阻尼受站姿變化影響的相對幅度較大;② 一些人體局部姿態如舉手、屈膝對測試者的等效自振頻率無明顯影響，但對等效阻尼比有較明顯影響。

圖5(a)為柔性振動臺二所測得的加速度時程曲線以及擬合曲線，作為對比，圖5(b)給出將人體集中質量與振動臺質量直接疊加的單自由度體系理論分析結果。由圖6可見，此時等效單自由度模型擬合誤差較大，但仍好于將人體視為單純質量的情形。

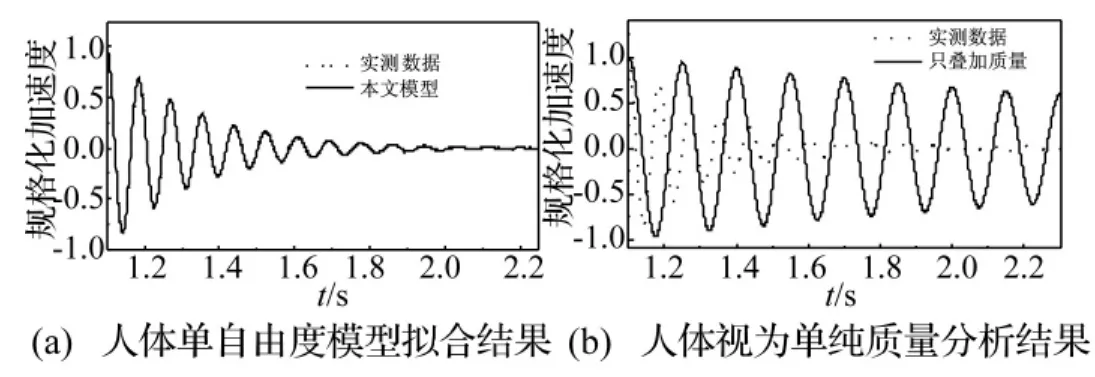
圖3 振動臺一:兩種簡化模型對比Fig.3 Comparison of two simplified models of human body on test rig 1

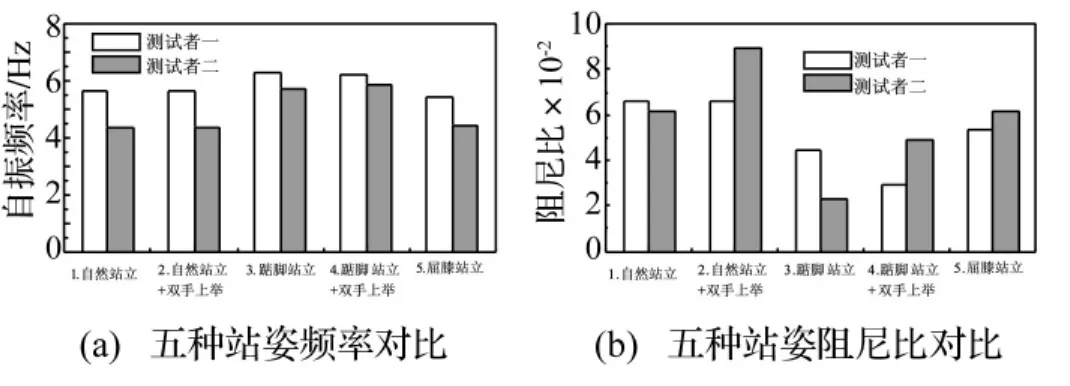
圖4 振動臺一:五種站姿自振參數Fig.4 Parameter identification of five standing postures on test rig 1

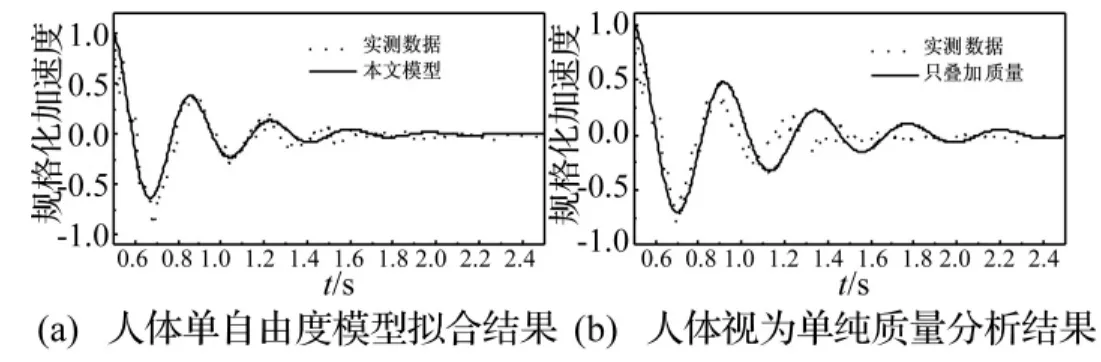
圖5 振動臺二:兩種簡化模型對比Fig.5 Comparison of two simplified models of human body on test rig 2

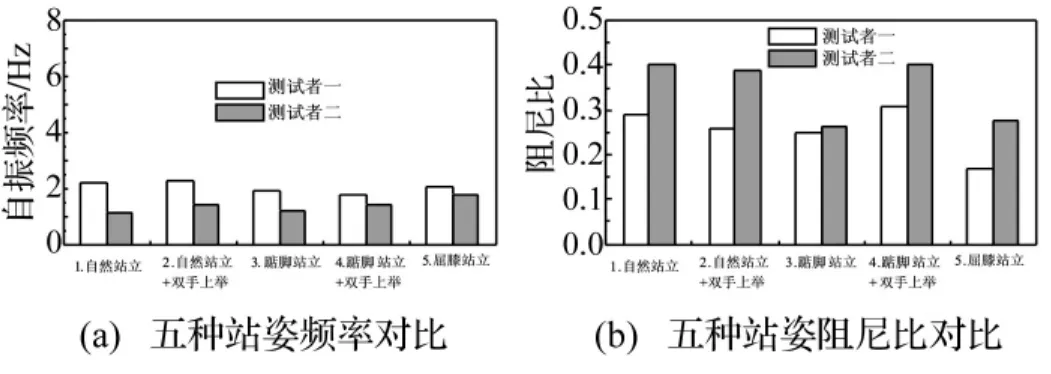
圖6 振動臺二:五種站姿自振參數Fig.6 Parameter identification of five standing postures on test rig 2

圖6 給出了五種典型站姿的參數識別情況(多次測試取平均值)，觀察圖6可得出與圖4類似的結論。但比較圖6與圖4可發現一些不同，即:① 柔性振動臺上測試導出的人體等效自振頻率(約2 Hz)要低于剛性振動臺上的相應數值(約4.5～6 Hz)，約為后者的1/3～1/2;② 柔性振動臺上測試導出的等效阻尼比(約0.3～0.4)遠高于剛性振動臺上的相應數值(約0.02～0.09)，最大差距可達到10倍以上。

綜合理論分析和實驗結果可知，若耦合振動體系的主振型參數發生變化，人體單自由度簡化模型參數取值也將隨之改變，但若站立的局部姿態變化不大可考慮忽略其影響。為便于工程應用，可根據實驗分析統計結果繪制相關圖表備查。

例如，圖7是通過調整振動臺參數對同一待測者進行測試，獲得的兩條簡化模型參數曲線，由圖7(a)可見，測試者等效自振頻率隨結構自振頻率和質量比在5～10 Hz之間變化，而由圖7(b)可見，測試者等效阻尼比也隨結構自振頻率和質量比在0.2～0.4之間變化。

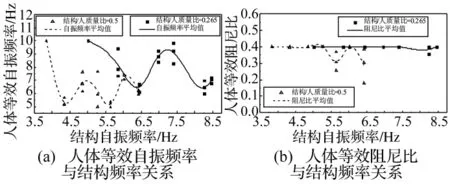
圖7 單自由度等效模型參數與結構參數關系Fig.7 Variation of equivalent human body parameters with structure parameters

4 結果驗證與結論

本文實驗中采用了初始位移激勵后測量擬合自由振動加速度時程的方法，這與國內外相關研究中采用的根據電液伺服振動臺掃頻分析結果對人體模型進行參數識別的原理有所不同，但所得結果仍有一些相似之處:

(1)在剛性較大的振動臺一上，兩位測試者自然站立的等效自振頻率分析結果在4.3～5.7 Hz范圍內變化，這與Subashi，Matsumoto，Griffin等在電液伺服振動臺上得出的人體直立時全身共振頻率約為5～6 Hz的結論[1]接近;

(2)研究中發現測試者雙手上舉對于等效自振頻率無明顯影響，這也和Subashi，Matsumoto，Griffin等在實驗中發現上肢姿態對人體共振頻率無明顯影響[1]一致;

(3)相似條件下，研究中得出的人體等效阻尼比波動范圍(0.2～0.4)與 Matsumoto，Griffin通過實驗得出的人體站姿阻尼比(0.3 ～0.5)[3]接近;

(4)研究中發現的當人體與結構質量比發生變化時，等效阻尼比隨之變化的現象在文獻[10]中也有類似論述。

綜上所述，根據理論分析結果、實驗測試擬合曲線及與前人理論的對比驗證情況，結論如下:

(1)由振型疊加法知，一般情況下不存在與人體精確多自由度模型動力學上完全等價的單自由度模型，但可通過調整其參數的辦法獲得與精確模型或實驗結果的最佳數值逼近;

(2)人體的局部姿態可影響其單自由度等效模型的參數取值，例如本文研究中踮起腳尖站立導致等效自振頻率增加，而舉手動作使得等效阻尼比發生變化;

(3)由前述可推知根據結構動力學參數確定人體等效單自由度模型參數顯然有利于獲得更為準確的動力學分析結果。

[1]Subashi G H M J，Matsumoto Y，Griffin M J.Modelling resonances of the standing body exposed to vertical wholebody vibration:Effects of posture[J].Journal of Sound and Vibration，2008，317:400 －418.

[2]Matsumoto Y， Griffin M J. Modelling the dynamic mechanisms associated with the principal resonance of the seated human body[J].Clinical Biomechanics，2001，16:31－44.

[3]Matsumoto Y，Griffin M J.Mathematical models for the apparent masses of standing subjects exposed to vertical whole-body vibration [J].Journal of Sound and Vibration，2003，260:431 －451.

[4]Wei L，Griffin M J.Mathematical models for the apparent mass of the seated human body exposed to vertical vibration[J].Journal of Sound and Vibration，1998，212(5):855－874.

[5]Griffin M J.Handbook of human vibration[M].London:Academic Press Limited，1990.

[6]何浩祥，閆維明，張愛林.人行激勵下梁板結構與人體耦合作用研究[J].振動與沖擊，2008，27(10):130－133.HE Hao-xiang，YAN Wei-ming，ZHANG Ai-lin.Dynamic interaction between human and beam-slab structures under human walking excitation[J].Journal of Vibration and Shock，2008，27(10):130 －133.

[7]Dougill J W，Wright J R，Parkhouse J G，et al.Human structure interaction during rhythmic bobbing[J].The Structural Engineer，21 November，2006:32 －39.

[8]陳建英，方之楚.人－結構相互作用動力學建模研究[J].振動與沖擊，2007，26(6):10－13.CHEN Jian-ying，FANG Zhi-chu.Study on modeling of human occupants-structure dynamic interaction[J].Journal of Vibration and Shock.2007，26(6):10－13.

[9]樊健生，李 泉，李全旺，等.考慮人－結構相互作用的樓蓋振動控制研究[J].振動與沖擊，2010，29(11):230－236.FAN Jian-sheng，LI Quan，LI Quan-wang，et al.Floor vibration control considering human-structure interaction[J].Journal of Vibration and Shock，2010，29(11):230 －236.

[10]Ebrahimpour A，Sack R L.Design live loads for coherent crowd harmonic movements[J].JournalofStructural Engineering，1992，118(4):1121 －1136.