薛澤春，李永剛，李連之，張憲璽，劉 穎

(1.山東省化學儲能與新型電池技術重點實驗室，山東 聊城 252059;2.聊城大學化學化工學院，山東 聊城 252059)

在進行色譜分析或光譜分析過程中，信號強度較弱或噪聲信號較強，會造成信噪比較小，使有用信號不能完全充分反映試樣的信息，或分析樣品含量很低，信號較弱，而應用小波變換，可發現合適信號［1］.目前，小波分析在故障診斷、圖像處理、語音識別、光譜分析［2］等領域得到了廣泛應用.在光譜分析中，由于小波分析具有優良的多分辨率分析特性［3］，利用小波多尺度分析可把信號分解成高頻和低頻成分，實現去噪功能［4］.

小波變換主要是基于小波時頻局域化特性，頻率成分在時間軸上位置保持不變，頻率變換不影響信號的線性［2，5－6］，能夠同時展現信號時間－頻率性質.在獲取試樣信號過程中，噪聲信號一般頻率較高，而有用信號頻率較低，小波變換可以將信號按頻率分開.

1 小波變換原理

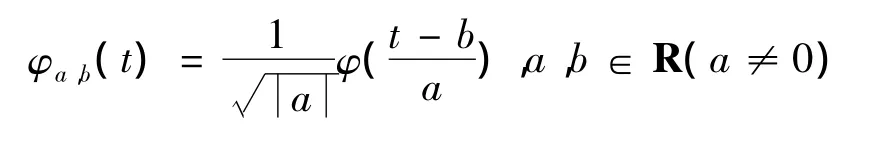
a用于控制伸縮，稱為尺度參數，b用于控制平移位置，稱為平移參數，φa，b(t)稱為小波函數.小波變換為某信號f(t)∈R在小波域的投影，通常定義為f(t)和φa，b(t)的內積，即:

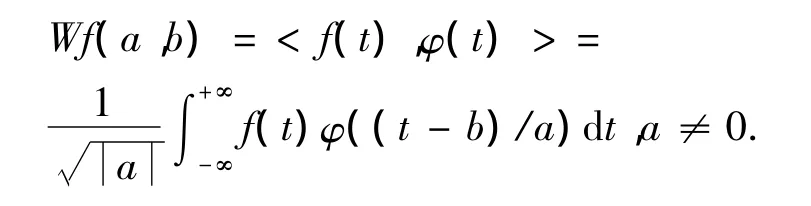
小波變換由于a，b可變且具有時頻局部化特征，因此對非平穩信號顯示出了獨特的分析能力.在小波分析中，隨著尺度因子a的增大，小波φa，b(t)的窗口逐漸加寬，在時間軸上考慮范圍大，而在頻域上相當于用低頻小波作概貌分析，對于較高頻率的噪聲信號濾波能力也隨之增強［10］.在低頻時，小波變換的時間分辨率較差，而頻率分辨率較高;在高頻時，小波變換的時間分辨率較高，而頻率分辨率較低.所以小波變換被譽為“數學顯微鏡”［11－12］.

小波基的選取應從一般原則和具體對象兩方面進行考慮.一般原則包括正交性，緊支集，對稱性，平滑性.要完全滿足以上特性是十分困難的，小波的選取也沒有形成統一的標準［13］.可以采用嘗試的方法從多個小波基中選取合適的小波.

連續小波變換可以在較大的伸縮尺度上觀察信號的變化趨勢，變換系數用小波函數與信號相似性程度表示.系數大說明信號與小波函數相似程度大，選擇小波系數可以重現原信號.在低尺度下，含有較多的噪聲信號，而在大尺度下基本上是要研究的信號，因此對小波系數累積求和，就可放大原信號.

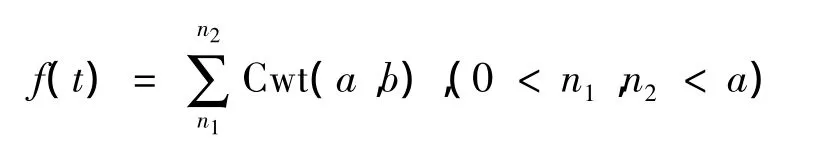
通過小波系數求和，就可以將噪聲中難以識別的信號強化，從而發現被原始信號掩蓋的信號.

2 實驗過程

2.1 模擬信號

分析信號多為高斯峰，應用Matlab模擬一信號，并且為噪聲信號所淹沒，不能有效進行定量定性分析.

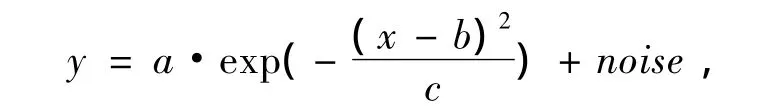
取a=2，b=200，c=40，noise為噪聲，信號譜圖如圖1所示.信號被噪聲完全覆蓋，不能有效區別有效信號，也不能進行定性、定量分析.

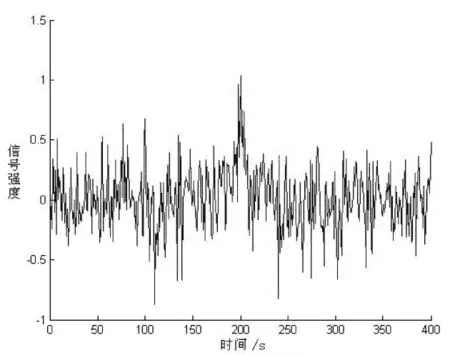
圖1 模擬信號

2.2 對信號進行連續小波變換

用 mexh，db4，coif4，haar，meyr，morl小波分別對圖1信號進行連續小波變換，并將變換系數求和，將弱信號放大，尋找最佳小波形式.

3 結果與討論

3.1 合適小波函數的選擇

用 mexh，db4，coif4，haar，meyr，morl小波對圖1信號進行連續小波變換，并將變換系數求和，放大信號如圖2所示.

從圖2 可以看出，a，b，c，f在時間為 200 處出現強峰，此處正好是模擬信號的峰位置，因此mexh，db4，coif4，morl能夠反映出信號位置，但是b，c，f雜峰比較多，不如 a平滑;d，e在時間為200處沒有出現信號峰，不能反映模擬信號的位置.綜上所述，最好選擇墨西哥帽小波進行小波變換.

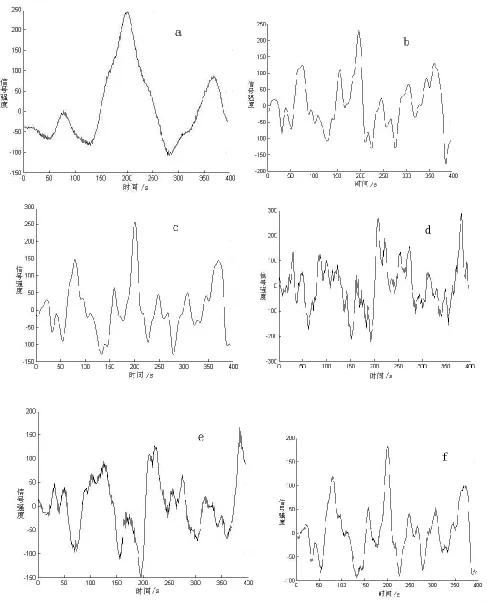
圖2 連續小波變換后小波系數求和(a ～ f小波函數分別為 mexh，db4，coif4，haar，meyr，morl)

3.2 連續小波變換找出有效信號

將模擬信號用墨西哥帽小波進行小波變換，尺度a取值為1∶96.如圖3所示，在低尺度，也就是頻率較高的信號，是噪聲信號的小波變換系數;在大尺度，是頻率較低的信號，是有效信號的小波變換系數.所以通過小波變換可以將混合信號按頻率分開.

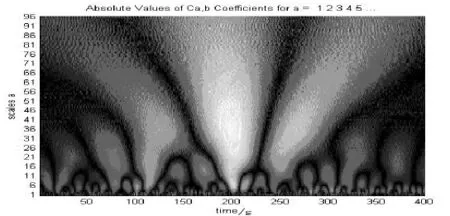
圖3 模擬信號連續墨西哥帽小波變換圖

在圖3中，顏色的深淺代表小波系數的大小，顏色越深小波系數越大.從圖3可以看出，信號在時間為200的點處，各尺度的小波系數最大，此處也正好是信號的位置，說明通過小波變換可以找到信號峰的位置.

3.3 弱信號的放大

除去高頻的噪聲信號將小波變換系數加和，就可以將原來的弱信號放大，而峰位值不變.圖4為不同尺度條件下求和后作圖.

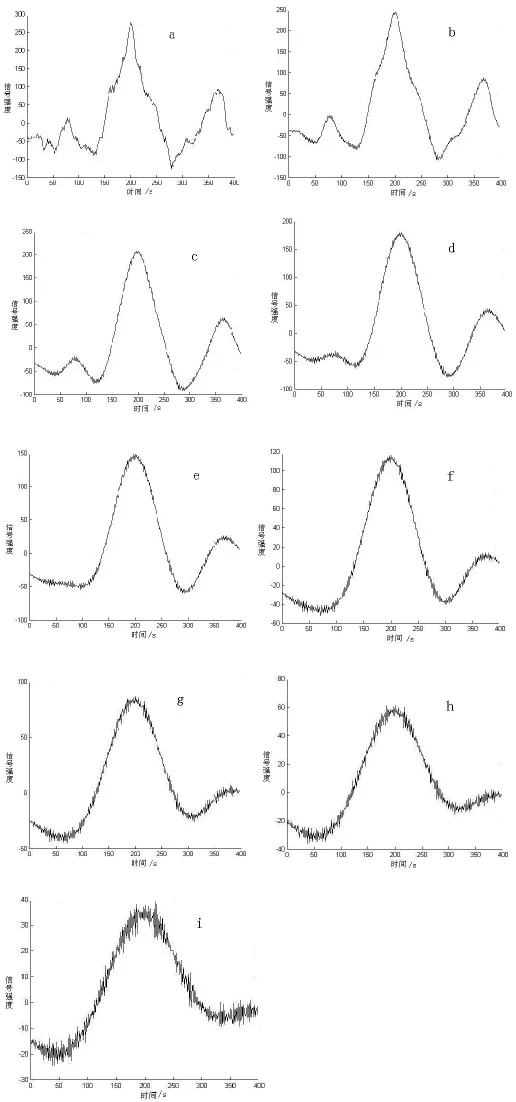
圖4 模擬信號連續墨西哥帽小波變換系數求和a～i分別為1～96、10～96、20～96、30～96、40～96、50～96、60～96、70～96、80～96小波系數之和)

從圖4可以看出，利用小波變換后系數求和可以放大原信號，但是求和范圍不同，所得圖形不一樣.范圍較小時，信號平滑性較差，不符合高斯線性關系;范圍較大時，信號夾雜很多噪聲信號，原因是連續小波變換會造成冗余信號.因此，通過觀察最好從c、d、e中選擇，這里我們選擇d來進行定量計算.

3.4 信號定量分析

將模擬信號按比例增大，然后用連續墨西哥帽小波變換，求其變換系數，加和以放大信號，研究其線性關系.

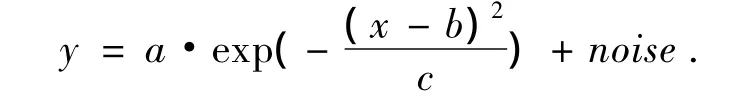
a=2，a=3，a=4，a=6，b=200，c=40分別作圖如圖5所示.

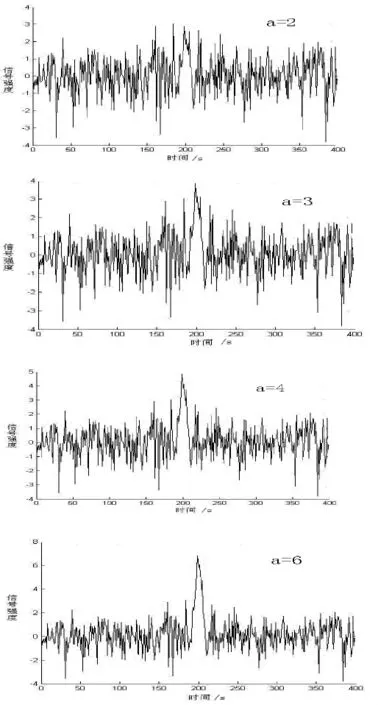
圖5 a=2，a=3，a=4，a=6 時模擬信號

在圖5中，有效信號被噪聲信號覆蓋，難于定量分析，將其用連續墨西哥帽小波變換，求其30～96層小波變換系數之和，并對時間作圖，如圖6所示.

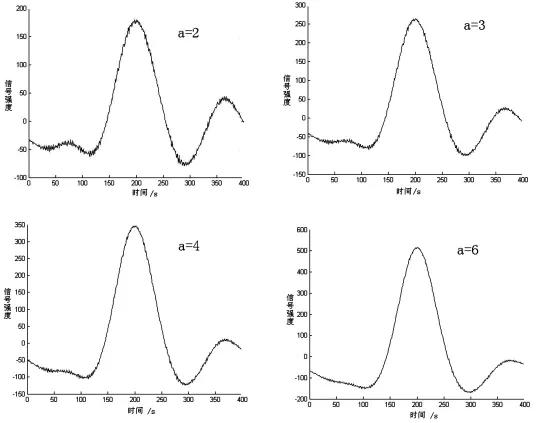
圖6 模擬信號小波系數之和與時間關系圖

在原始模擬信號中不能觀察到的信號通過小波變換被放大，峰位值不變，并且能夠進行定性定量分析.

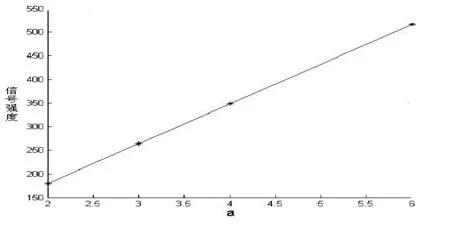
圖7 信號強度與a值線性關系曲線

4 結語

弱信號分析是分析化學的一個重要方向.將信號通過連續墨西哥帽小波變換，頻率高的噪聲信號在尺度因子較小的位置，頻率較低的信號在尺度因子較大的位置.通過連續墨西哥帽小波變換能同時展現信號的時－頻信息的特點，從而能夠找出有用信號，將埋藏在噪聲信號中的有用信號小波變換系數加和，可以將弱信號放大，信號強度不同，小波變換系數加和也不同，并且具有良好的線性關系，能夠作為定性定量分析的依據.

［1］盧禮萍，朱旭東，魏良淑，等.不同輻照下大豆胰蛋白酶抑制劑熒光的小波分析［J］.甘肅農業大學學報，2011，46(2):147 －151.

［2］朱殿明，金萬祥，駱曉森，等.人血清卟啉熒光光譜的雙正交樣條小波識別［J］.光譜學與光譜分析，2008，28(8):1879－1881.

［3］顧振普，鄭廣.心電信號小波分析［J］.河北科技大學學報，2006，27(4):328－331.

［4］周丹，王欽軍，田慶久，等.小波分析及其在高光譜噪聲去除中的應用［J］.光譜學與光譜分析，2009，29(7):1941－1945.

［5］宋寧，周新勇，徐曉軒，等.基于小波變換的藻類顯微光譜成像分類技術［J］.發光學報，2007，28(6):954－958.

［6］王書濤，王玉田，車仁生，等.基于小波變換的葉綠素熒光光譜測量系統研究［J］.應用光學，2005，26(1):49－ 52.

［7］倪雪春，楊慧中.基于小波變換測定水質中硝酸鹽含量［J］.光譜實驗室，2009，26(5):1175 －1178.

［8］張悅，杜守軍，張麗梅.小波奇異性在鋼結構損傷檢測中的應用［J］.河北科技大學學報，2010，31(2):151－157.

［9］郁青春，張世超，王新東，等.小波變換方法消除熱重實驗噪音信號［J］.北京科技大學學報，2007，29(5):532－536.

［10］陳昌國，龍英，李納.化學信號小波變換的本質分析［J］.渝西學院學報:自然科學版，2003，12(14):5－8.

［11］楊福生.小波變換的工程分析與應用［M］.北京:科學出版社，1999:89－90.

［12］馬麗萍，石炎福，余華瑞.小波分析及其在化工信號分析處理中的應用及展望［J］.化工進展，2005，24(2):147－153.

［13］劉素美，李書光.超聲檢測信號處理的小波基選取［J］.無損探傷，2004，28(6):12 －15.