時間序列中隨機型缺失數據的填補及預測效果比較*
李濟賓 張 熙 張晉昕
時間序列中隨機型缺失數據的填補及預測效果比較*
李濟賓1,2張 熙3張晉昕1△
目的 本文旨在通過填補時間序列資料中的隨機型缺失數據并擬合ARIMA模型,比較三種填補方法的填補和預測效果。方法 利用SAS產生平穩、有周期性的時間序列并構造不同比例的隨機型缺失,分別采用周期性填補法、均值填補法和三次樣條函數插值法進行缺失數據的填補,并對填補后序列擬合ARIMA模型進行序列預測。采用配對t檢驗對三種填補方法的填補誤差和序列預測誤差進行比較。結果 三種填補方法的填補值與真值的差異均無統計學意義(P>0.05);隨著缺失比例的增大,周期性填補法的填補誤差和序列預測誤差均小于三次樣條函數插值法和均值填補法。結論 周期性填補法對于含有確切周期信息的時間序列缺失數據,填補效果較優。
缺失數據 時間序列 填補 周期性 三次樣條
1.中山大學公共衛生學院醫學統計與流行病學系(510080)
2.香港中文大學公共衛生與基層醫療學院
3.復旦大學公共衛生學院衛生統計與社會醫學教研室(200032)△通訊作者:張晉昕,E-mail:zhjinx@mail.sysu.edu.cn
缺失數據是醫學應用研究中普遍存在的實際問題。在對醫學時間序列數據進行建模預測時,序列的長度和完整性對擬合模型的可靠性有影響。醫學時間序列的觀測值具有不可重復的特點,缺失數據的隨意插補或跳過,使擬合的模型難以很好地反映縱向數據的規律,制約了時間序列在醫學領域的應用。因此,如何合理填補時間序列資料中的缺失數據,進而擬合合適的數學模型是醫學時間序列應用中需要解決的一個重要問題。
目前,針對時間序列缺失數據處理的技術主要基于時域信息,如刪除法、均數填補法、極大似然估計法、三次樣條函數插值法等〔1,2〕。實踐表明,三次樣條函數插值法是一種思路簡明、效果較優的補缺方法。這些方法共有的一個缺陷是,未能利用時間序列中蘊含的周期信息。為此,本文探討一種基于序列周期信息,以不同周期的譜峰值作為權重的缺失數據填補方法,并利用模擬時間序列數據考核其填補效果。
資料與方法
1.模擬序列
在SAS9.1的軟件環境下,利用正弦函數Y=abs(sin(ωx))和正態分布函數 ε=μ+sqrt(σ2)×rannor(seed),模擬產生μ=0,σ2=1,隨機波動水平的月度時間序列,序列的周期設置為3、6和12個月。序列的起始時間設為1962年1月1日。模擬序列長度設置為N=300。
隨機型缺失數據的構造:利用SAS為模擬時間序列數據產生正態分布的隨機數,根據隨機數的秩次依次將缺失數據的比例設置為5%,10%,15%,20%,25%,30%,35%,40%共8個檔次。
2.缺失數據填補方法
(1)均值填補法:以序列均數作為缺失數據的填補值。
(2)三次樣條函數插值法〔2〕
三次樣條函數插值法是時間序列中缺失數據填補的常用方法之一。設函數f(x)在給定區間[a,b]上有定義,其中a=x0<x1<…<xn=b是給定的n+1個插值節點,若S(x)滿足條件:①S(x)在每個小區間[xj,xj+1]上是三次多項式;②S(x)在每一個內節點上,S(x)∈C2[a,b];③S(x)在所有節點內滿足S(xj)=f(xj)。則稱S(x)是節點x0,x1,…,xn上的三次樣條函數。為了構造特定的樣條插值函數,還需增加邊界條件的限制。邊界條件可根據實際情況來確定,不同邊界條件下S(x)的表達式可以有多種表現形式。本文針對時間序列的三次樣條函數插值法,由SAS9.1軟件環境下的PROC EXPAND過程實現〔3〕。
(3)基于序列周期信息的填補法(下文簡稱作周期性填補法)
①以序列均值作為缺失數據的初始填補值;②利用周期圖峰值檢驗的方法搜索序列中有統計學意義的m個隱周期,用I1,I2,…,Im表示對應周期的譜峰值;③基于m個周期,分別計算不同周期位置上序列的均數,將第i個缺失位置上的m個均數記為Xi(1),…,Xi(m);④ 以周期峰值I1,I2,…,Im作為權重,獲得第i個缺失位置的加權填補值Xi:

式中i表示缺失數據序號i=1,2,…,n,j表示隱周期序號j=1,2,…,m;
⑤用步驟④中填補后的完整序列,重復步驟②、③和④,直到前后兩次填補值的相對改變量δ≤0.01或迭代次數大于100次時,停止迭代,獲得缺失數據的最終填補值。本文通過搜索周期圖的峰值個數來確定隱周期的初始個數r,周期性檢驗的方法采用Priestley(1981)和Chiu(1989)提出的檢驗統計量〔4〕。
3.填補效果比較
(1)填補誤差
采用均方根誤差(RMSE)和平均絕對誤差〔5〕(MAE)量化填補值與真實值之間的填補誤差。
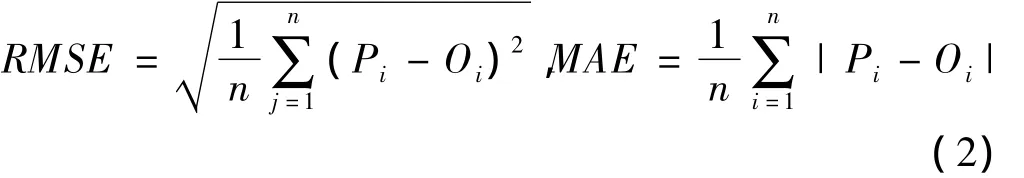
其中,n為缺失數據序號i=1,2,…,n,Pi表示填補值,Qi表示真實值。
以缺失個數n為樣本量,用配對t檢驗比較各填補方法的填補值與真值的差異;同時調整檢驗水準為α'=α/2=0.05/2=0.025,比較均值填補法、三次樣條函數插值法與周期性填補法的絕對填補誤差(|真實值-填補值|)的差異。
(2)絕對預測誤差
采用自回歸移動平均求和模型進行時間序列的模型擬合及序列預測,簡記為 ARIMA(p,d,q),其表達式為〔6〕:
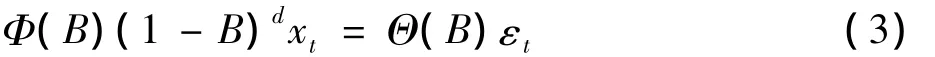
式中,p和q分別表示自回歸和移動平均的階數,d為差分的階數,Φ(B)=1-φ1B-…-φpBp,為p階自回歸系數多項式。Θ(B)=1-θ1B-…-θqBq,為q階移動平均系數多項式。
按照時間順序逐段選擇觀測長度為120的序列片段,進行提前期l=1~12的預測(即t1=1~120,t2=2~121,…),直至預測末期觀測值為時間序列的末值,確保能夠從實測值得到預測誤差。以推移次數(n')作為樣本量,以三種方法的絕對預測誤差(絕對預測誤差=|真實值-預測值|)作為變量,進行配對t檢驗,比較均值填補法、三次樣條函數插值法與周期性填補法絕對預測誤差的差異(其中檢驗水準調整為α'=α/2=0.05/2=0.025)。絕對預測誤差小的填補方法,其填補效果較優。
結 果
1.不同缺失比例下三種方法的填補值與真值的差異
表1結果顯示,三種方法的填補值與真值之間的差異均無統計學意義(P>0.05)。進一步繪制不同缺失比例下,三種方法填補值的平均誤差線圖。圖1顯示,周期性填補方法的曲線與參考線間的距離最小,而三次樣條函數插值法的曲線與參考線間的距離最大。
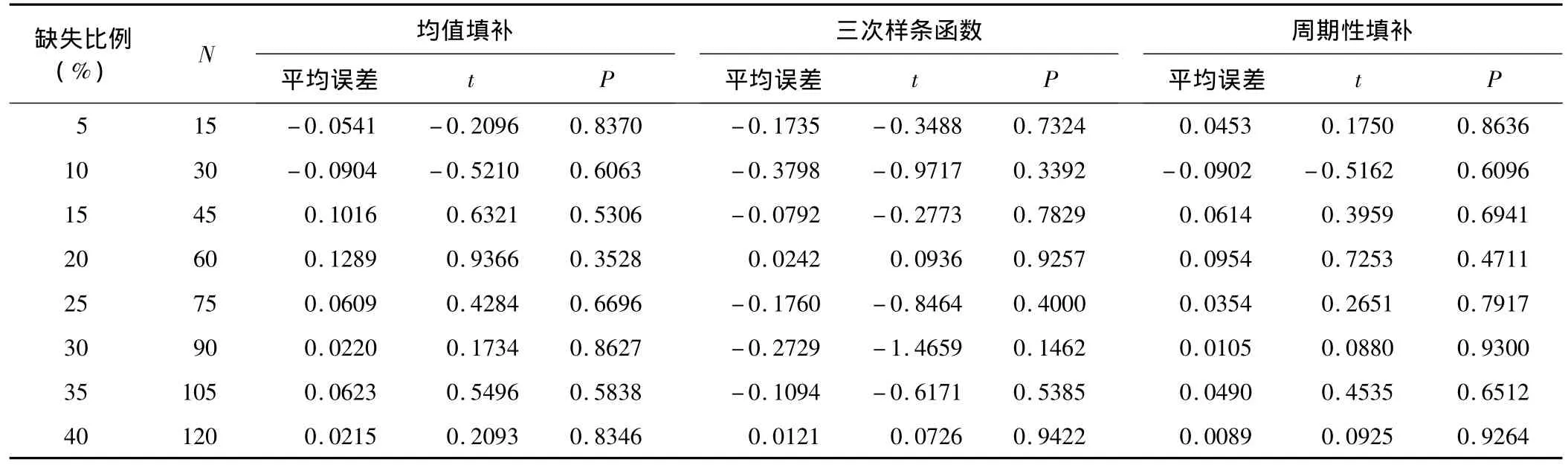
表1 不同缺失比例下三種方法的填補值與真值的比較
2.不同缺失比例下三種方法填補誤差的比較
表2為均值填補法、三次樣條函數插值法與周期性填補法的絕對填補誤差的比較結果。當缺失比例大于15%時,周期性填補法的絕對誤差小于均值填補法(P<0.025);此外,在各缺失比例下,周期性填補法的絕對誤差均小于三次樣條函數插值法對應的絕對誤差(P<0.025)。
圖2為不同缺失比例下,三種填補方法填補值的平均絕對誤差(a)和均方根誤差(b)的曲線圖,周期性填補方法的平均絕對誤差和均方根誤差的曲線均始終位于均值填補法和三次樣條函數插值法所對應曲線的下方。
3.缺失數據填補后序列擬合模型的預測誤差比較
為了進一步比較三種方法的填補效果,由序列自相關函數和偏自相關函數,對模擬時間序列進行模型識別,最終確定原始序列的模型形式為:

圖1 不同缺失比例下三種填補方法填補值的平均誤差

利用此模型對三種方法填補后的完整序列建模并進行提前期l=1~12的預測。在中期(l=6)和遠期(l=12)的預測中,除缺失比例等于10%的情況,周期性填補法填補序列對應的預測誤差均小于均值填補法和三次樣條函數插值法。此外,在近期(提前期l=1)的預測中,當缺失比例大于10%時,周期性填補法填補序列對應的預測誤差小于均值填補法。
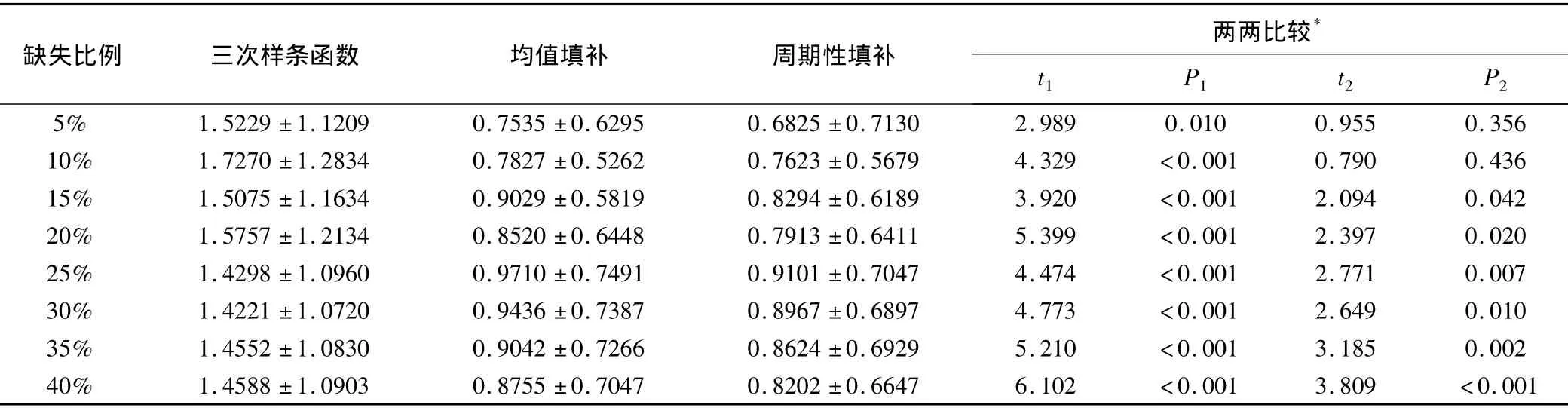
*:1:三次樣條函數與周期性填補;2:均值填補與周期性填補。
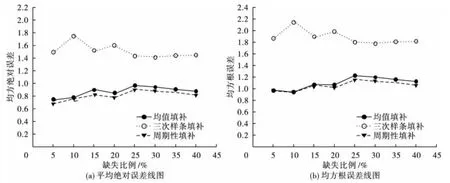
圖2 三種填補方法的平均絕對誤差、均方根誤差隨缺失比例變化的線圖
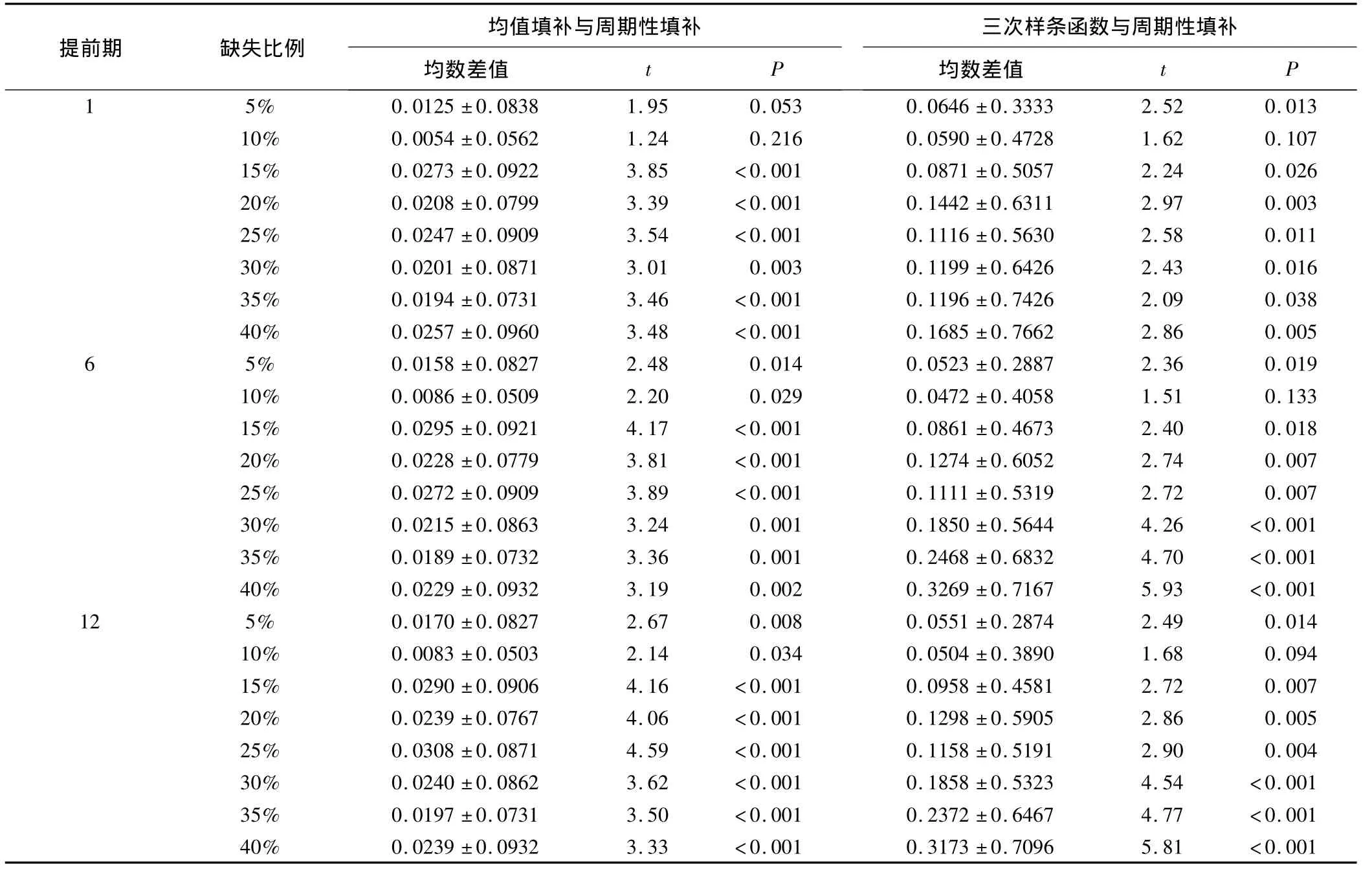
表3 提前1、6、12期時三種填補方法在各缺失比例下的預測絕對誤差 (n'=169)
圖3顯示,在缺失比例小于10%的情況下,三種方法的絕對預測誤差的差別不大;隨著缺失比例的增大,三次樣條函數插值法的絕對預測誤差呈上升趨勢;均值填補法和周期性填補法的絕對預測誤差均減小。同時,趨勢圖顯示周期性填補法所對應預測誤差的曲線始終位于均值填補法和三次樣條函數插值法所對應曲線的下方。
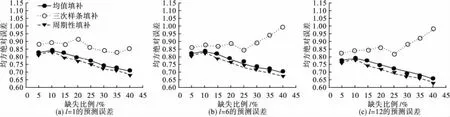
圖3 不同缺失比例下,三種填補方法提前期l=1、6、12的平均絕對預測誤差變化趨勢
討 論
時間序列數據是按照時間順序取得的一系列觀測值,其典型的特征是相鄰觀測值之間存在相關性,使得時間序列觀測值相互間不獨立,從而致使通常的針對獨立數據的缺失數據填補方法在時間序列中不再適用。
本文針對基于時間序列周期信息的缺失數據加權填補方法〔7〕,利用模擬數據從填補誤差和預測誤差兩個方面對填補方法的填補效果進行考核。結果顯示,三種方法的填補值均可以較好地估計出真實值,同時缺失比例大于15%時,周期性填補法的填補誤差是三種方法中最小的。在提前期l=1、6、12的預測中,缺失比例大于10%以后,周期性填補法填補序列的預測誤差小于均值填補法和三次樣條函數插值法。此外,對于均值填補法,由于樣本均數在不同位置的多次出現,容易導致低估變量的變異程度,進而扭曲原始樣本的分布狀態〔8-9〕。
綜上所述,結合時間序列的周期信息,進行加權填補的效果優于普通的只利用時域信息的缺失數據填補方法,尤其是對于缺失比例較大的情況。另外,需要說明的是,周期性檢驗是“周期性填補法”的關鍵步驟之一,對于未蘊涵確切周期信息的時間序列,周期性填補法將不再適用。
1.Wayne FV,Suzanne MC.A comparison of missing-data procedures for ARIMA time-series analysis.Educational and Psychological Measurement,2005,65(4):596-615.
2.郭昌言,高尚.三次樣條函數插值的推廣.科學技術與工程,2011,11(7):1507-1509.
3.高惠璇等編譯.SAS系統SAS/ETS軟件使用手冊.北京:中國統計出版社,1998,232-252.
4.Michael Arits,Mathias Hoffmann.The detection of hidden periodicities:a comparison of alternative methods.Paper provided by European University Institute in its series Economics WorkingPapers with number ECO2004/10.
5.Heikki Junninena,Harri Niskaa,Kari Tuppurainenc,et al.Methodsfor imputation of missing values in air quality data sets.Atmospheric Environment.2004(38):2895-2907.
6.肖枝洪,郭明月.時間序列分析與SAS應用.武漢:武漢大學出版社,2009,44-109.
7.張熙.基于周期信息的時間序列缺失值填補方法研究.廣州:中山大學,碩士學位論文,2009.
8.RK Kunar,RM Chadraseker.Missing data imputation in cardiac dataset(survival prognosis).IJCSE,2010,2(5):1836-1840.
9.王睿.胃食管反流病流行病學調查及其缺失數據的處理方法研究.上海:第二軍醫大學,博士學位論文,2009.
Prediction and Imputation for Missing Data at Random in Time Series
Li Jibin,Zhang Xi,Zhang Jinxin.School of Public Health,Sun Yat-sen University(510080),Guangzhou
ObjectiveIt is aimed to compare the effects of interpolation and prediction by imputing the missing data at random and fitting proper ARIMA models in time series.MethodsMissing data at random are generated with different missing proportions in simulated stationary time-series with periodicity.And then the missing data are interpolated using mean imputation,the cubic spline imputation and imputation based on periodicity.Prediction for imputed time-series is carried out by fitting a proper ARIMA model.The differences of interpolation and prediction from truth-data were analyzed using paired t test.ResultsThe differences between interpolation and truth-data were of no statistical significance.Both absolute interpolation errors and prediction errors in imputation based on periodicity were less than those of the cubic spline imputation and the mean imputation.ConclusionThe imputation based on periodicity showed better efficiency for missing data at random in time series with significant periodicity.
Missing data;Time series;Imputation;Periodicity;Cubic spline
2008年國家自然科學基金資助(30872182)

