應變率對復合材料殼體外壓性能的影響①

侯 曉，秦 誼，何高讓，王凌云

(1.中國航天科技集團公司四院，西安 710025;2.中國航天科技集團公司四院四十一所，固體火箭發動機燃燒、熱結構與內流場國防科技重點試驗室，西安 710025)

0 引言

潛射導彈在水下高速運行時，彈體表面會產生空泡，當導彈穿越水面時，因介質突變，空泡發生潰滅，引起導彈力學環境急劇變化。空泡潰滅時間約為5 ms［1］，復合材料殼體在此過程中受到沖擊外壓載荷的作用。國內外學者對復合材料殼體的外壓穩定性問題進行了廣泛的研究。Smerdov［2］基于經典薄殼理論通過對鋪層角度進行優化，提出提高復合材料殼體外壓載荷的方法。Han等［3］基于一階剪切理論研究了對稱鋪設圓柱殼在側向外壓和靜水外壓載荷作用下的屈曲特性。杜建科等［4］采用非線性屈曲理論，在不考慮幾何缺陷和材料缺陷的條件下，利用ANSYS軟件對纖維纏繞復合材料殼體和燃燒室側壓穩定性進行了對比計算。Ouellette等［5］給出了纖維纏繞材料圓管在側向壓力作用下的屈曲荷載計算方法，指出對復合材料圓柱殼結構進行外壓屈曲分析時必須考慮初始幾何缺陷的影響。周承倜等［6］使用能量法和有限差分法分析了多層復合材料圓柱薄殼在靜水壓力作用下的屈曲性能，考慮了初始幾何缺陷、幾何非線性和材料的物理非線性等因素對臨界載荷的影響。王永志等［7］對復合材料旋轉殼的失穩問題進行了有限元推導，考慮了橫向剪切變形的影響，認為橫向剪切變形對復合材料構件的結構穩定性影響較大。李志敏［8］運用了邊界層理論對纖維增強各向異性層合剪切圓柱殼的屈曲進行了分析，分析中同時考慮了前屈曲非線性變形，后屈曲大撓度和初始幾何缺陷的影響以及橫向剪切變形和耦合剛度的影響。這些研究都是針對準靜態外壓載荷進行的研究，對作用時間按毫秒等級計量的外壓載荷來說，還需考慮加載速率的影響。

對大部分材料而言，載荷的加載速率對材料的力學性能均有不同程度的影響，一般用應變率來描述。周元鑫等［9］研究了不同應變率下石墨纖維增強鋁合金基體復合材料的拉伸性能，研究結果表明該材料具有明顯的應變率強化效應。陳思穎等［10］研究了炭纖維、玻璃纖維和Kevlar纖維的拉伸力學性能的應變率相關性進行，結果是幾種纖維的彈性模量無一例外地隨應變率的增大而增大。蔣邦海等［11－12］對炭纖維增強復合材料試件的應變率相關性進行了試驗和研究，結果表明復合材料的強度性能不但存在應變率效應，而且這種效應是各向異性的。

目前，對固體火箭發動機復合材料殼體外壓承載能力的研究都在準靜態加載條件下進行，對其動態力學性能的研究較少。按照類似的原理，復合材料殼體對動態外壓載荷的承載能力應高于靜態外壓承載能力，如果能夠得到復合材料殼體應變率與外壓載荷定量或定性相關關系，按殼體動態外壓承載能力進行設計，可減輕復合材料殼體的質量，提高發動機質量比。正是基于這一考慮，本文對復合材料殼體外壓載荷承載能力與應變率的相關關系進行了試驗和分析。

1 試驗件和試驗方法

1.1 試驗件設計

按相同設計和工藝狀態研制了9臺試驗件，其中3臺進行靜態外壓試驗，6臺進行動態外壓試驗。試驗件赤道間距200 mm，直徑 φ200 mm，壁厚1.6 mm，前后裙采用了鋁合金材料，試驗件結構如圖1所示。

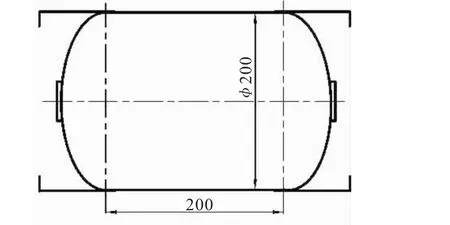
圖1 復合材料殼體試驗件Fig.1 Composite case sample

1.2 試驗方法介紹

如圖2所示，將試驗件置于 φ350 mm ×550 mm的試驗容器內，試驗件一端與試驗容器固支連接，另一端用堵蓋密封。向容器內注入水介質，通過手動壓力泵和航天四院設計的脈沖壓力發生器向容器內加載靜態外壓和脈沖外壓，手動壓力泵上連接觀察用壓力表。試驗件表面粘貼有應變片，試驗容器壁上安裝測壓傳感器。

靜態外壓試驗時，系統的采集頻率設定為10 Hz;動態外壓試驗時，系統的采集頻率設定為2 000 Hz。要求靜態外壓試驗在3～5 min內完成，脈沖外壓發生器具有在200 ms內達到1 500 kPa以上的能力(估算值)。試驗現場環境氣壓為98 kPa。

圖2 外壓試驗裝置Fig.2 Expermental system of external pressure

2 靜態外壓承載能力計算

試驗過程中實際對試驗件施加了軸外壓載荷。首先利用公式法對該試驗件的靜態軸外壓承載能力進行計算。根據文獻［13－15］，理論臨界失穩外壓按式(1)計算，理論臨界失穩軸壓按式(2)計算。該試驗狀態下殼體同時受軸外壓聯合載荷的作用，應滿足式(3)關系。

式中 E1、E2分別為殼體縱、環向彈性模量;μ1、μ2分別為縱、環向泊松比;R、h、L分別為殼體直徑、壁厚和赤道間距;T、P分別為殼體實際承受的軸壓和外壓。

聯立式(1)～(3)，參數T用加載壓強表示，代入試驗件的設計參數，求得殼體的最大失穩壓強為631 kPa。該計算值為理論值，根據文獻［14－15］，由于材料缺陷和幾何缺陷等原因，采用線性理論導出的理論臨界應力計算公式不能直接用于工程實際，必須進行修正。文獻［14］根據實際試驗結構給出鋼圓筒臨界外壓計算時的修正系數為0.8。復合材料的均勻性比鋼材料差，修正系數應選取的更低一些。文獻［15］中復合材料殼體臨界軸壓計算時修正系數應按0.3～0.5選取。本試驗中試驗件的制作要比一般的工程結構件精細，修正系數更高一些。試驗中主要加載載荷為外壓載荷，綜合考慮，修正系數取0.72，則計算臨界失穩壓強為454 kPa。

3 靜態外壓試驗

在靜態外壓試驗初始加載階段，隨載荷增加，壓力表讀數逐漸增大;當載荷加載到一定值后聽到復合材料破壞的響聲，同時壓力表的壓力值達到最大;繼續加載，壓力值開始下降。由此判斷試件破壞，試驗終止。

3臺試驗件的試驗結果見表1。表1列出了測試壓強(絕壓)和相對壓強(平衡大氣壓強后試件的實際承載壓強)。No.2試件的相對壓強與計算結果相同，No.1、No.3試件的試驗結果均略小于計算結果，說明修正系數的選取略高。

表1 靜、動態外壓試驗結果Table 1 The results of external pressure in static and dynamic condition

圖3為3臺殼體靜態軸外壓試驗測試系統加載曲線。由圖3可見，初始加載階段試件表面載荷按拋物線上升，到最大值時加載源雖然仍繼續加載，但測試壓強開始下降。測試系統曲線與試驗現場壓力表監視結果一致。壓強下降的原因是由于殼體外壓失穩后卸壓所致。加載曲線開始下降的時刻即為失穩破壞時刻，對應載荷為殼體失穩破壞載荷。

圖4為No.3試件部分測點應變測試結果(No.1、No.2試件測試結果類似)。由圖4可知，在第68 s時刻殼體局部應變快速增加，70 s時刻部分點達到最大值。由于加載源仍在繼續，其中一點應變繼續增大，表明該點所在部位出現了較大變形，試驗后解剖證實該點對應部位破壞。應變測試結果表明，該試件在70 s時刻開始失穩，74 s時刻完全失穩破壞，完全失穩破壞時的最大應變在－3 600 με左右。

圖3 靜態外壓載荷-時間曲線Fig.3 External pressure-time curves in static condition

圖4 No.3應變測試曲線Fig.4 Strain curves of No.3 sample

由以上加載和應變測試曲線分析知，3臺殼體的破壞值分別為 399、454、433 kPa，加載時長為 47、49、70 s，均可視為準靜態加載。

4 動態外壓試驗

動態外壓試驗時，沖擊外壓加載系統可實現10～200 ms脈沖外壓加載。

4.1 空載調試

動態外壓試驗前首先進行空載調試。空載調試的目的是為了確定加載載荷隨時間變化的趨勢以及加載源所能提供的最大加載壓強，試驗得到的加載載荷－時間曲線見圖5。由圖5可知，該試驗條件下加載載荷為一脈沖波形，峰值載荷絕壓可達到1 864 kPa，去除環境壓強影響后，實際加載壓強為1 766 kPa，可滿足加載要求。

圖5 空載試驗載荷-時間曲線Fig.5 Load-time curve of the no-load test

4.2 負載調試

為保證試驗條件的完全一致，排除加載容器內不同儲水量對試驗結果的影響，正式試驗前又進行了帶試件的調試試驗。調試試件的外形幾何尺寸與正式試件完全相同，但將殼體的壁厚設計的較厚，剛性較大，調試試驗結果見圖6。由圖6可知，帶試件狀態下，加載載荷也為一脈沖波形，峰值最大絕壓壓強可達到1 761 kPa，去除環境壓強影響后，實際加載壓強為1 663 kPa。

空載調試和負載調試時，加載載荷都可達到靜態試驗值的3倍以上，可滿足試驗條件。

圖6 帶試件調試空載試驗載荷-時間曲線Fig.6 Load-time curve of the test with sample

4.3 正式試驗

按照調試試驗的狀態對6臺正式產品進行了動態外壓試驗，試驗結果見表1，加載載荷-時間曲線見圖7。

圖7 動態外壓載荷-時間曲線Fig.7 External pressure-time cures in dynamic loads test

從圖7看出，6次試驗中，加載載荷均為脈沖壓強波，實際加載壓強為564～725 kPa(相對壓強)，低于調試試驗值1 663 kPa，也低于空載調試試驗值1 766 kPa。對比空載調試和相同幾何尺寸試件調試結果分析知，沖擊加載系統提供的能量遠高于殼體試件的實際承載能力，當加載載荷不斷上升并達到殼體試件的臨界外壓時，殼體開始失穩并釋放了一定的空間，測試壓強曲線開始下降，其變形過程與靜態外壓試驗時相同。從以上分析知，圖7中各試件加載峰值點載荷即為試件的動態外壓承載能力，試驗平均值為667 kPa。6臺殼體加載載荷上升很快，以計時時刻計算，加載上升段時間為20～56 ms，基本達到了快速加載的目的。

試驗過程中對應變進行了測試，圖8為No.7殼體應變測試結果，其他殼體基本類似。從圖8可看出，對應載荷曲線峰值點44 ms時刻部分測點的應變趨近于最大值，部分測點的應變值繼續增大，表明該時刻殼體對應部位破壞。

圖8 動態外壓試驗應變-時間曲線Fig.8 Strain-time curve in dynamic loads test

5 試驗結果分析

5.1 失穩應變的確定

外壓試驗中(存在附加軸壓)，復合材料殼體的主要破壞形式是失穩破壞，因此對應變的分析應以負應變為準。動態加載過程中，部分應變測點的測試值(負應變)持續上升，然后在－4 000 με左右完全失穩破壞。靜態加載時由于手動泵加載方式為間歇式加載，完全失穩時刻的最大應變與開始失穩時相差2 s。動、靜態外壓試驗過程中完全失穩破壞的應變在－4 000 με左右。

5.2 應變率的確定

動態試驗過程中6臺試驗件載荷上升段時間為20～56 ms，其中20 ms和56 ms各出現1次，其他均在30～44 ms之間。按平均加載時間38 ms計算，應變按前述 －4 000 με 計算，則應變率為 0.105 s－1。

5.3 應變率對承載能力的影響

從動、靜態外壓試驗對比結果看，復合材料殼體試驗件動態軸外壓承載能力明顯高于靜態時的承載能力。承載能力提高的原因是由于材料的模量具有應變率相關性。

取3臺靜態試驗殼體相對壓強均值429 kPa作為該殼體在準靜態軸外壓載荷作用下的承載能力，取6臺動態試驗殼體相對壓強均值667 kPa作為該殼體在動態軸外壓載荷作用下的承載能力，則當應變率為0.105 s－1時，承載能力由 429 kPa 提高到 667 kPa，動態加載下承載能力是靜態下1.55倍。

6 結論

(1)復合材料殼體的外壓(同時加載了附加軸壓)承載能力具有應變率相關性，應變率提高，承載能力相應增加。

(2)用靜態試驗結果評判殼體對沖擊類載荷的承載能力是不恰當的，承受動載荷作用的結構，應以相應載荷條件下的試驗結果為依據，否則將造成結構的冗余設計，降低效率。

(3)試驗證明，直徑200 mm、壁厚1.6 mm的復合材料殼體，當應變率達到達到0.105 s－1等級時，承載能力是靜態環境下的1.55倍。

［1］羅金玲，毛鴻羽.導彈出水過程中氣/水動力學的研究［J］.戰術導彈技術，2004(4):23-25.

［2］Smerdov A A.A computational study in optimum formulations of optimization problems on laminated cylindrical shells for buckling II－ Shells under external pressure［J］.Composites Science and Technology，2000，60:2067-2076.

［3］Han B，Simitses G J.Analysis of anisotropic laminated cylindrical shells subjected to destabilizing loads，Part II:numerical results［J］.Composite Structures，1991，19:183-205.

［4］杜建科，田曉耕，沈亞鵬，等.復合材料燃燒室均布側壓下穩定性分析［J］.固體火箭技術，2002，25(2):18-21.

［5］Ouellette P，Hoa S V，Sankar T S.Buckling of composite cylinders under external pressure［J］.Polymer Composites，1986，7:363-374.

［6］周承倜，周建平.多層復合材料圓柱殼的非線性失穩計算［J］.應用數學和力學，1986，7(1):17-23

［7］王永志，向錦武.復合材料旋轉殼穩定性有限元分析和橫向剪切變形的影響分析［J］.復合材料學報，2006，23(4):175-179.

［8］李志敏.船舶與海洋工程中復合材料圓柱殼結構屈曲和后屈曲行為研究［D］.上海交通大學，2008.

［9］周元鑫，張學峰，夏源明.應變率對Gr/Al金屬基復合材料力學性能的影響［J］.爆炸與沖擊，1999，19(3):243-249.

［10］陳思穎，黃晨光，段祝平.幾種高性能纖維束的沖擊動力學性能試驗研究［J］.爆炸與沖擊，2003，23(4):355-359.

［11］蔣邦海，張若棋.一種炭纖維織物增強復合材料應變率相關的各向異性強度準則［J］.爆炸與沖擊，2006，26(4):333-338.

［12］蔣邦海，張若棋.動態壓縮下一種炭纖維織物增強復合材料的各向異性力學性能試驗研究［J］.復合材料學報，2005，22(2):109-115.

［13］陳盛秒.外壓容器涉及的公式法及其應用［J］.壓力容器，2008，25(11):30-33.

［14］黃啟珍，等.導彈結構·材料·強度(下)［M］.北京:宇航出版社，1996.

［15］陳汝訓.復合材料殼體的軸壓穩定性［J］.固體火箭技術，2001，24(1):13-15.