飛行器系統參數變化對章動過程的影響分析①

劉平安，郜 冶，王 革

(哈爾濱工程大學航天工程系，哈爾濱 150001)

0 引言

小衛星發射的最末級通常使用旋轉固體火箭發動機作為動力裝置，在旋轉飛行器固體火箭發動機工作過程中，隨著推進劑的燃燒，系統的質量逐漸減少，使得系統的質量特性與能量特性發生變化，最終導致了飛行器章動的增長［1－7］。為了深入理解章動過程中能量損失的作用效果，需對系統能量耗散過程進行研究。能量耗散是指物體在做回旋運動時的彈性振動所產生的效果。這種耗散會導致進動角θ產生一個偏離，且越來越大。一個軸對稱的物體旋轉時，遵守轉動慣量守恒，如果沒有這種彈性振動，就不會產生進動角的耗散作用。若不存在外部力矩，它將以恒定的姿態保持穩定的進動。若施加一個力矩，這個進動角就會增加，當力矩的作用停止，進動角的增加也隨之停止，將保持一穩定值。

物體旋轉時，如果沒有能量耗散，轉動慣量的最大軸和最小軸都是穩定的。當存在能量耗散時，只有轉動慣量的最大軸是穩定的。這時，當物體圍繞轉動慣量最小軸旋轉時，進動角將會繼續增大，直到改變運動姿態，圍繞轉動慣量最大軸旋轉。當飛行器的側向轉動慣量大于軸向轉動慣量，對常用的細長體結構來說，是固有的、不穩定的。

本文從能量耗散的角度出發，研究飛行器系統參數變化對章動效果的影響。

1 控制方程

在沒有外力矩作用的情況下，質量特性不變的彈性體做回旋運動時，歐拉動力學方程如下:

角動量矢量可表示為

旋轉動能可表示為

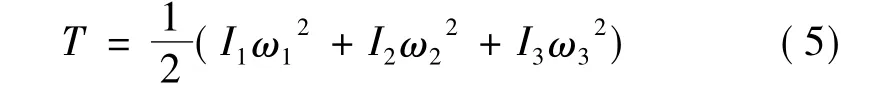
對于軸對稱飛行器，記作I1=I2=I，角動量值的平方可表示為

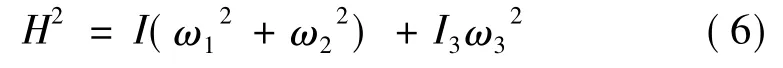
轉動動能可化簡為

由式(6)、式(7)可得:

由于 H=Iω3/cosθ，式(8)可表示為

對旋轉動能求時間的導數:

由式(10)可看出，章動角的變化率依賴于系統動能的變化率。隨著系統動能的耗散，章動角的變化率可增可減，取決于轉動慣量各分量的大小。對于實際的飛行器，由于推進劑的燃燒，伴隨著燃氣流的噴出，產生了噴氣阻尼作用，系統的能量發生了變化，動能的變化率不再為零。由于質量的損失，產生了能量的耗散，章動角速率也會發生變化。由于系統經歷了質量的減少及相應的噴氣阻尼作用，歐拉動力學方程可表示如下:

在飛行器系統不受外力矩作用的情況下，3個方向的歐拉方程可表示為

化簡可得:

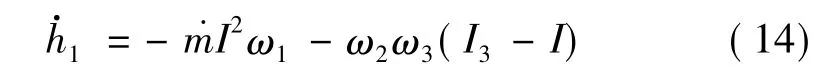
把角動量表達式帶入方程(14)～(16)，寫成角速度變化率的函數:

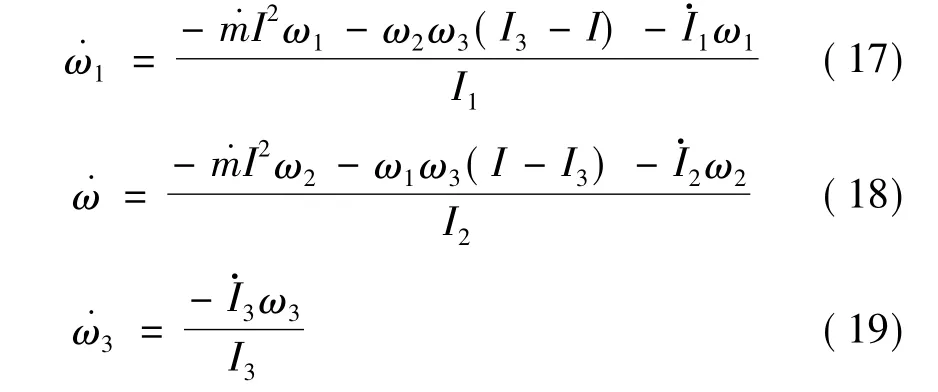
方程(17)～(19)是系統的角速度方程，描述了飛行器系統在質量減少、能量耗散過程中三向角速度的變化率。通過求解這3個方程，可得到章動變化過程中三向角速度的變化。

盡管章動角度發生了變化，在每一瞬時，角動量矢量與其分量在數值上保持相同的關系，即 H=Iω3/cosθ。這時，對式(9)進行求導，化簡可得到飛行器系統的能量耗散方程:

從式(20)可看出，旋轉飛行器系統，隨著質量減少，引起了系統能量的耗散，章動角的變化率依賴于系統動能的變化率。

當考慮質量變化時，對系統的轉動動能求導化簡可求得章動角的變化率:

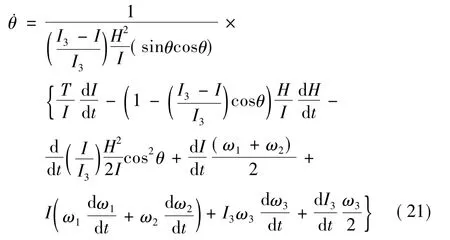
方程(21)是系統的章動方程，表達了在考慮旋轉飛行器系統質量變化，及其帶來的噴氣阻尼作用的條件下系統章動角的變化率。通過求解方程(21)，可得到系統章動角隨時間的變化歷程，或增大或減小。

至此，推導了旋轉飛行器工作過程中，伴隨著固體推進劑的燃燒，飛行器總的質量減少，引起了系統能量的耗散，以及相應的角速度與章動角的變化，得到了飛行器系統的角速度方程與章動方程。通過方程(17)～(19)可求解三向角速度的變化，通過方程(21)可求解章動角的變化。

2 計算結果與分析

2.1 算例1與分析

針對WESTAR-V飛行器，求解其角速度方程與章動方程。采用文獻［8］中的方法，在飛行器的工作過程中，將系統具體參數的變化，包括轉動慣量、質量流量、平均燃燒室半徑與質心位置(質心到噴管出口的距離)，根據實際數據用公式擬合成時間的函數。

側向轉動慣量:

軸向轉動慣量:

平均燃燒室半徑:

質心位置(質心到噴管出口的距離):

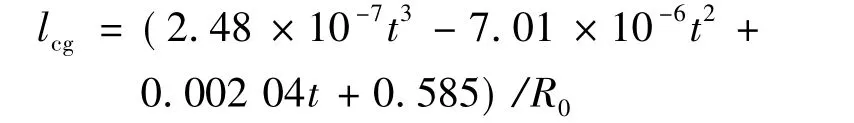
發動機的質量流量:

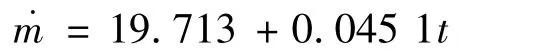
把這些參數代入角速度方程與章動方程，用四階的龍格庫塔法求解，計算結果見圖1～圖3。

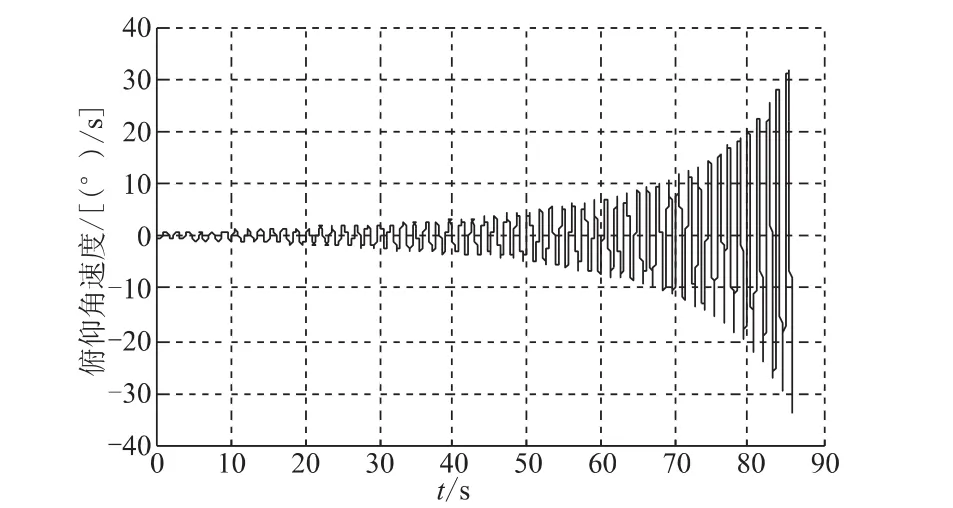
圖1 WESTAR-V俯仰角速度隨時間的變化Fig.1 Chang of pitch angular rate of WESTAR-V

從圖1和圖2可知，WESTAR-V飛行器俯仰角速度與偏航角速度的相位相差90°。飛行器系統隨著推進劑的燃燒，質量逐漸減少，引起了系統能量的耗散，使得系統的俯仰角速度與偏航角速度逐漸增加，到燃燒結束時達到最大值，在30°/s附近。實際飛行器系統的俯仰角速度與偏航角速度［9］的變化見圖4和圖5。可看出，由計算得到的結果與實際飛行器俯仰角速度與偏航角速度的變化規律一致，都呈現出了側向角速度的增長。

圖2 WESTAR-V偏航角速度隨時間的變化Fig.2 Chang of yaw angular rate of WESTAR-V

圖3 WESTAR-V章動角隨時間的變化Fig.3 Chang of nutation angular rate of WESTAR-V

圖4 WESTAR-V飛行器俯仰角速度隨時間的變化Fig.4 Chang of pitch angular rate of WESTAR-V spacecraft

從圖3可知，WESTAR-V飛行器的章動角以近似指數的形式增加，從初始的0.9°增加到燃燒結束時刻的17°，這與實際的飛行器數據一致［9］。章動角的迅速增大是飛行器系統由于質量變化引起能量耗散的結果。

從算例1可知，從飛行器系統質量變化引起能量耗散的角度出發，推導得到的角速度方程與章動方程，可正確描述飛行器旋轉章動過程中的角速度變化與章動角變化趨勢。計算結果與實際數據趨勢的一致性也說明了所采用的計算方法是可信的。可使用該方法計算具有旋轉章動不穩定性的飛行器的參數變化，研究飛行器其他參數變化對飛行器系統角速度變化與章動角變化的影響。

圖5 WESTAR-V飛行器偏航角速度隨時間的變化Fig.5 Chang of yaw angular rate of WESTAR-V spacecraft

2.2 算例2與結果分析

改變WESTA-V飛行器的參數，考察參數變化對飛行器章動過程的影響。首先，考察發動機質量流量的變化對飛行器章動過程的影響，保持其他參數不變，將質量流量減小、增大，求解章動角與側向角速度。其中，減小的質量流量為˙m1=15.331+0.045 1 t，增大的質量流量為˙m2=24.095+0.045 1 t。

當質量流量減小時，俯仰角速度的變化如圖6所示，偏航角速度的變化如圖7所示，俯仰角速度與偏航角速度在燃燒結束時達到最大，在18°/s左右，兩者的相位相差90°。與 WESTAR-V飛行器相比(30°/s左右)，側向角速度明顯降低。章動角的變化如圖8所示，從初始的0.9°增加到燃燒結束時刻的 15.5°，小于WESTAR-V飛行器的最大章動角(17°)。可見，當質量流量減小時，使得飛行器的側向角速度的變化幅值減小，最大章動角減小，從而削弱了飛行器的章動效果。

當質量流量增大時，俯仰角速度的變化如圖9所示，偏航角速度的變化如圖10所示。俯仰角速度與偏航角速度在到燃燒結束時達到58°/s左右，兩者的相位相差 90°。與 WESTAR-V飛行器相比(30°/s左右)，側向角速度明顯增大。

圖6 質量流量減小時的俯仰角速度Fig.6 Pitch angular with mass rate decreasing

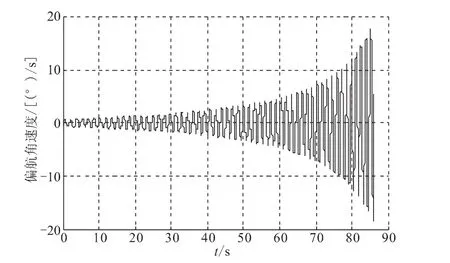
圖7 質量流量減小時的偏航角速度Fig.7 Yaw angular with mass rate decreasing

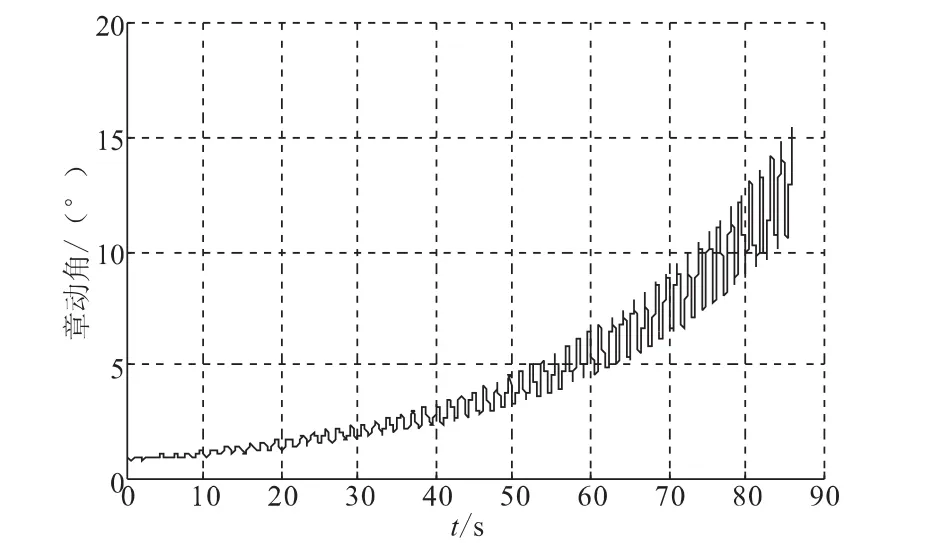
圖8 質量流量減小時的章動角Fig.8 Nutaion angular with mass rate decreasing

圖9 質量流量增大時的俯仰角速度Fig.9 Pitch angular with mass rate increasing

圖10 質量流量增大時的偏航角速度Fig.10 Yaw angular with mass rate increasing

章動角的變化如圖11所示，從初始的0.9°增加到燃燒結束時刻的23.3°，明顯大于WESTAR-V飛行器的最大章動角(17°)。可見，當質量流量增加時，使得飛行器的側向角速度的變化幅值增大，章動角也大大增加，從而加強了飛行器的章動效果。

圖11 質量流量增大時的章動角Fig.11 Nutation angular with mass rate increasing

從改變發動機的質量流量的計算結果可看出，發動機質量流量的變化在很大程度上影響了章動效果。隨質量流量的增加，飛行器的章動效果明顯加強。實際上，隨飛行器型號的逐漸增大，必然采用更大尺寸的火箭發動機，以獲得更大的推力，也就決定了發動機的質量流量隨之增加。在STAR-48發動機之前，采用小型號的發動機STAR-37，由于推力小，質量流量小，并沒有發生明顯的章動放大行為。在STAR-48發動機之后，采用尺寸更大的發動機STAR-63，由于推力增加，質量流量增加，發生了更加嚴重的章動放大行為。這就從側面印證了隨發動機質量流量的增加，會增加飛行器的章動效果。

考察質心位置的變化對飛行器章動效果的影響，保持其他參數不變，將質心位置減小與增大，求解章動角與側向角速度。lcg1是增大的質心位置，lcg2是減小的質心位置，lcg則是ESTAR-V飛行器實際的質心位置。其中:

當質心位置減小時，俯仰角速度的變化如圖12所示，偏航角速度的變化如圖13所示。俯仰角速度與偏航角速度在燃燒結束時達到16°/s左右，與WESTARV飛行器相比(30°/s左右)，側向角速度明顯降低。章動角的變化如圖14所示，章動角從初始的0.9°增加到燃燒結束時刻的15.1°，小于WESTAR-V飛行器的最大章動角(17°)。可見，當質心位置減小，使得飛行器的側向角速度的變化幅值減小，最大章動角減小，從而削弱了飛行器的章動效果。

圖12 質心位置減小的俯仰角速度Fig.12 Pitch angular with centroid position decreasing

圖13 質心位置減小的偏航角速度Fig.13 Yaw angular with centroid position decreasing

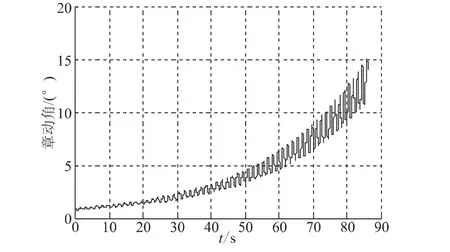
圖14 質心位置減小的章動角Fig.14 Nutation angular with centroid position decreasing

當質心位置增大時，俯仰角速度的變化如圖15所示，偏航角速度的變化如圖16所示。俯仰角速度與偏航角速度在燃燒結束時達到59°/s左右，與WESTARV飛行器相比(30°/s左右)，側向角速度明顯增大。章動角的變化如圖17所示，從初始的0.9°增加到燃燒結束時刻的23°，明顯大于WESTAR-V飛行器的最大章動角(17°)。可見，當質心位置增大，使得飛行器的側向角速度的變化幅值增大，章動角也大大增加，從而加強了飛行器的章動效果。

從改變飛行器質心位置的計算結果可看出，飛行器質心位置的變化與發動機質量流量的變化一樣，在很大程度上影響了章動效果。隨質心位置的增大，飛行器的章動效果明顯加強。從角速度方程(17)、(18)可看出，側向角速度的變化率是受噴氣阻尼項的影響。隨發動機質量流量與質心位置的增大，噴氣阻尼項也逐漸加大，對側向角速度變化率的影響也會加大。由計算結果可知，當發動機質量流量與質心位置增大，側向角速度隨之增大，相應的章動角也隨之增大，章動效果加強。可看出，噴氣阻尼項對飛行器的章動過程起到了驅動作用，而不是阻尼作用。或者說，噴氣阻尼項對章動過程所起的驅動作用超過了其所起的阻尼作用，最終表現為驅動作用，而不是文獻中提到的阻尼作用。

圖15 質心位置增大的俯仰角速度Fig.15 Pitch angular with centroid position increasing

圖16 質心位置增大的偏航角速度Fig.16 Yaw angular with centroid position increasing

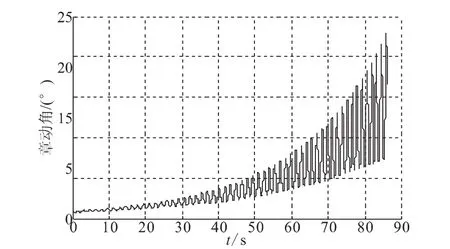
圖17 質心位置增大的章動角Fig.17 Nutation angular with centroid position increasing

當考察軸向轉動慣量的變化對飛行器章動過程的影響時，保持其他參數不變，將軸向轉動慣量減小、增大，求解章動角的變化。發現隨軸向轉動慣量由小到大變化，飛行器系統的章動角大幅度減小，章動效果明顯削弱。可見，增大飛行器系統的軸向轉動慣量，有利于抑制飛行器系統的章動。

當考察側向轉動慣量的變化對飛行器章動過程的影響時，保持其他參數不變，將側向轉動慣量增大、減小求解章動角的變化。發現隨側向轉動慣量由小到大的變化，飛行器系統的章動角大幅度增加，章動效果明顯加強。可見，若要抑制飛行器系統的章動，需減小飛行器系統的側向轉動慣量。

從算例2可知，飛行器系統的章動過程受系統軸向轉動慣量、側向轉動慣量、質量流量與質心位置等參數變化的影響。通過改變這些參數的變化，可改變飛行器系統的章動效果。當增大飛行器系統軸向轉動慣量，減小側向轉動慣量，減小質心位置，減小發動機質量流量，可削弱飛行器系統的章動效果;反之，可增強飛行器系統的章動效果。所以，在設計飛行器系統時，可通過設計飛行器系統的參數，如軸向轉動慣量、側向轉動慣量、質量流量與質心位置等，以便減小、削弱潛在的可能發生的章動現象。

3 結論

在旋轉飛行器工作過程中，伴隨著固體推進劑的燃燒，從飛行器系統質量減少，引起的能量耗散出發，推導得到了飛行器系統的角速度方程與章動方程，并通過適當的方法求解。通過具體算例驗證了所推導的角速度方程與章動方程，可正確描述飛行器旋轉章動過程中的角速度變化與章動角變化。計算結果與實際數據趨勢的一致性，也說明了所采用的計算方法是可信的。使用該方法計算具有旋轉章動不穩定性的飛行器的參數變化，研究了飛行器其他參數變化對飛行器系統角速度變化與章動角變化的影響。發現飛行器系統的章動過程受系統軸向轉動慣量、側向轉動慣量、質量流量與質心位置等參數變化的影響。通過改變這些參數的變化，可改變飛行器系統的章動效果。當增大飛行器系統軸向轉動慣量，減小側向轉動慣量，減小質心位置，減小發動機質量流量，可削弱飛行器系統的章動效果;反之，可增強飛行器系統的章動效果。通過具體算例驗證了上述觀點，所得結論可為具有旋轉章動不穩定性的飛行器系統參數設計提供指導。

［1］Janssens F.Jet damping and nutation growth during the burn of a solid rocket motor such as PAM-D［J］.ESA Journal，1988，12:273-288.

［2］Eke F O，Mao T C.On the dynamics of variable mass systems［J］.The International Journal of Mechanical Engineering Education，2002，30(2):123-137.

［3］Eke F O，Mao T C，Morris M J.Free attitude motions of a spinning body with substantial mass loss［J］.Journal of Applied Mechanics，2004(71):190-194.

［4］Jeerapa Sookgaew.Effects of substantial mass loss on the attitude motion of a spinning rocket［D］.University of California，2004:13-23.

［5］郜冶，楊丹，熊永亮.旋轉飛行器固體火箭發動機引起的章動不穩定性分析［J］.宇航學報，2008，29(1):270-275.

［6］楊丹，郜冶，熊永亮.旋轉固體火箭發動機隨質量變化的姿態運動分析［J］.推進技術，2008，29(1):8-12.

［7］郜冶，劉平安，楊丹.旋轉固體火箭發動機飛行器章動不穩定機理述評［J］.固體火箭技術，2011，34(1):14-18.

［8］Tina Morina Rice.Application of energy analysis to the problem of propulsion driven nutation instability of spin stabilized spacecraft［D］.The University of Tennessee，2006:18-36.

［9］Flandro G A.Characteristics of nutation instability in ULYSSES/PAM-S spin stabilized spacecraft［R］.CA 92647，1987:30.