淺析北京市2012屆上半年期中、期末對導數及其應用的考查

☉陜西省榆林市第一中學 韓向杰

考向一、對導數的概念及導數基本應用的考查

命題規律：以選擇題、填空題等客觀題目的形式考查導數的基本概念、運算、導數的物理意義、幾何意義及利用導數與不等式研究函數的單調性.

1.（2012年昌平區高三期末考試理8）已知定義在R上的函數f（x）滿足f（2）=1，f′（x）為f（x）的導函數.已知y=f′（x）的圖像如圖1所示，若兩個正數a，b滿足（f2a+b）>1，則的取值范圍是（ ）.

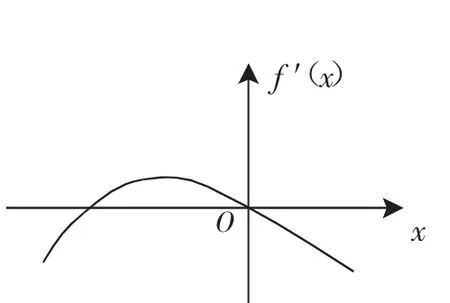
圖1

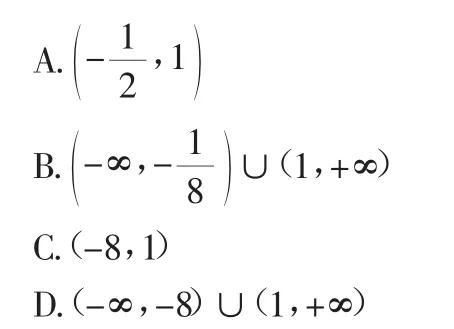
答案：A.

2.（2012年西城區高三期末考試文11）若曲線y=x3+ax在原點處的切線方程是2x-y=0，則實數a=______.

答案：2.

3.（2012年順義區高三尖子生綜合素質展示10）設函數f（x），g（x）在（0，5）內導數存在，且有以下數據：

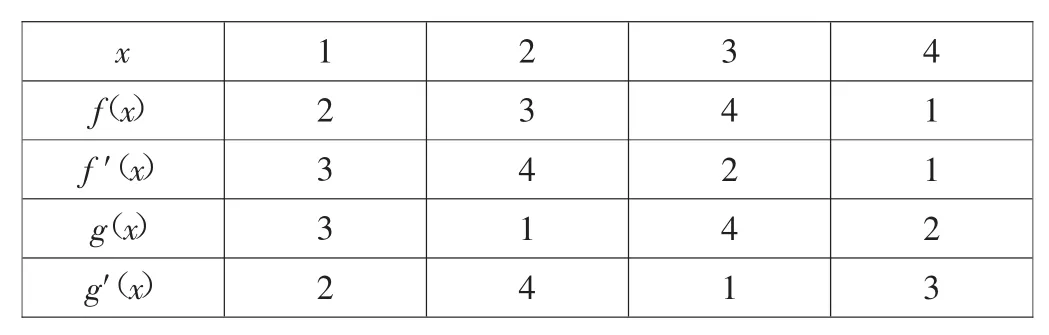
2 3 4 3 4 1 4 2 1 1 4 2 4 1 3 1 2 3 3 2 x f（x）f′（x）g（x）g′（x）

則曲線在點（1，f（1））處的切線方程是______；函數f（g（x））在x=2處的導數值是______.

答案：y=3x-1，12.

點評：主要考查復合函數的求導法則，化歸與轉化的思想，將函數的單調性問題轉化為不等式恒成立的問題.

考向二、導數與極值、最值

命題規律：利用導數求函數的極值與最高值是高考常見的題型，要注意極值與最值的區別，本內容也最常用于實際問題.

4.（2011年海淀區高三年級第一學期期中練習文17）某工廠生產某種產品，每日的成本C（單位：萬元）與日產量x（單位：噸）滿足函數關系式C=3+x，每日的銷售額S（單位：萬元）與日產量x的函數關系式

已知每日的利潤L=S-C，且當x=2時，L=3.

（Ⅰ）求k的值；

（Ⅱ）當日產量為多少噸時，每日的利潤可以達到最大，并求出最大值.

當x≥6時，L=11-x≤5.

所以當x=5時，L取得最大值6.

所以當日產量為5噸時，每日的利潤可以達到最大值6萬元.

5.（2011年東城區高三示范校高三綜合練習（一）理17）已知f（x）=xlnx，g（x）=-x2+ax-3.

（Ⅰ）求函數f（x）在［t，t+2］（t>0）上的最小值；

（Ⅱ）對一切x∈（0，+∞），2f（x）≥g（x）恒成立，求實數a的取值范圍.

解：（Ⅰ）f（x）定義域為0，+（）∞，f′（x）=lnx+1，

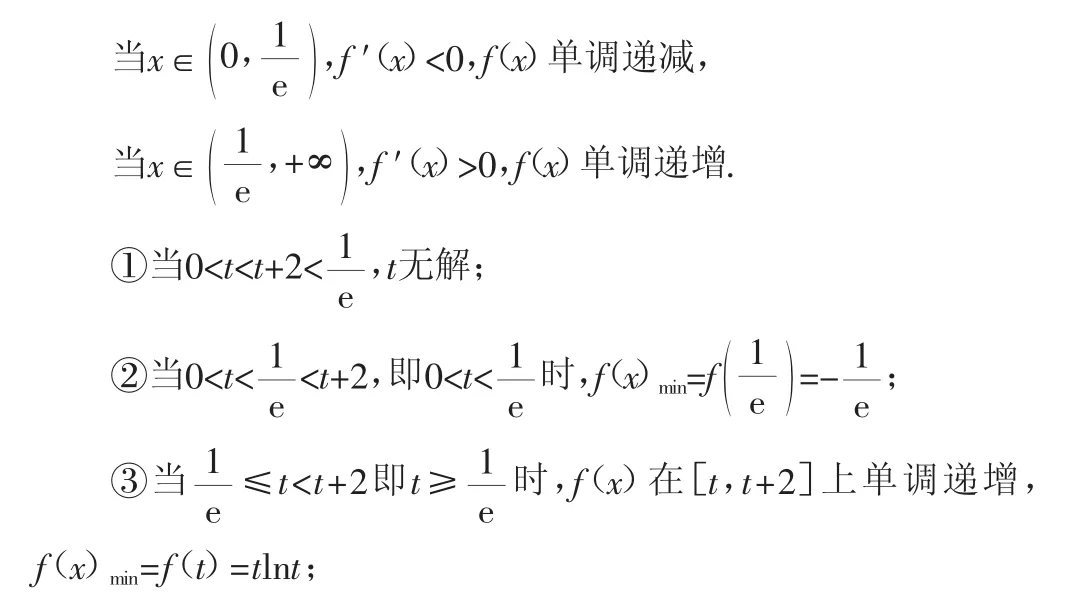
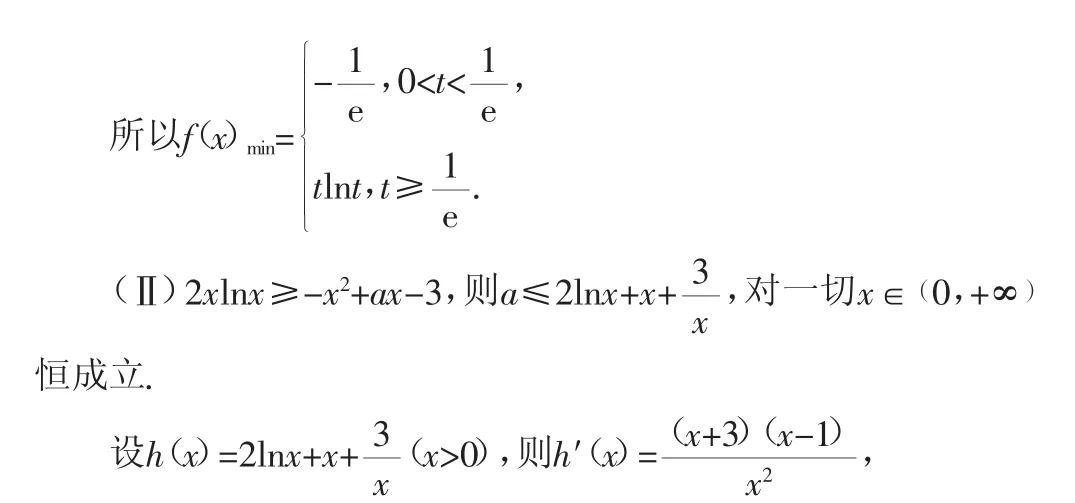
當x∈（0，1），h′（x）<0，h（x）單調遞減.

當x∈（1，+∞），h′（x）>0，h（x）單調遞增.

h（x）在（0，+∞）上，有唯一極小值h（1），即為最小值.

所以h（x）min=h（1）=4，因為對一切x∈（0，+∞），2f（x）≥g（x）恒成立，所以a≤h（x）min=4.

6.（2012年順義區高三尖子生綜合素質展示18）已知函數f（x）=x2+ax-lnx,a∈R.

（Ⅰ）若a=0時，求曲線y=f（x）在點（1，f（1））處的切線方程；

（Ⅱ）若函數f（x）在［1，2］上是減函數，求實數a的取值范圍；

（Ⅲ）令g（x）=f（x）-x2，是否存在實數a，當x∈（0，e］（e是自然對數的底）時，函數g（x）的最小值是3？若存在，求出a的值；若不存在，說明理由.

解：（Ⅰ）當a=0時f（x）=x2-lnx.

（Ⅰ）當a=1時，試求函數f（x）在區間［1，e］上的最大值；

（Ⅱ）當a≥0時，試求函數f（x）的單調區間.

解：（Ⅰ）函數f（x）的定義域為（0，+∞）.

所以函數f（x）在區間［1，e］上單調遞增，則當x=e時，函數（fx）取得最大值

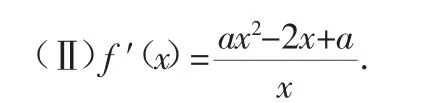
當a=0時，因為f′（x）=-2<0，所以函數f（x）在區間（0，+∞）上單調遞減；

當a>0時，⑴當Δ=4-4a2≤0時，即a≥1時，f′（x）≥0，所以函數f（x）在區間（0，+∞）上單調遞增.

⑵當Δ=4-4a2>0時，即00解得：

點評：本類型的題目主要考查函數的性質、導數、不等式等基礎知識，考查分析推理和知識的綜合應用、轉化的能力.