高三立體幾何復習教學中的探究性學習

☉江蘇省泰州市民興實驗中學 郭金華

在高三數學立體幾何復習中，我們從“以人為本，主動發展”的教學理念出發，將課堂教學設計為探究性學習組織教學，發揮了較好的效果.探究性學習主要分為兩個過程：一是問題引動，加強雙基；二是主動探究，培養能力.現以立體幾何復習中的“角度、距離的計算”一節課的教學為例，分析如下.（限于篇幅，本文主要側重于二面角）

一、巧設問題，加強基礎訓練

加強雙基，夯實基礎是復習目標之一.對于基礎知識的復習，由于學生已經有了第一次學習的經歷，無論理解的程度如何，總是以為自己是知道的，若仍按照教師提問學生答，教師羅列學生抄，教師歸納學生聽的復習方法，勢必讓學生感到乏味.時間花費多，學生收效少.我們采取“問題引動”法，即在教學過程中，圍繞教學內容，設計問題組，引導學生主動復習基礎知識，掌握基本方法.

如在“角度、距離的計算”一節復習中，首先設計如下問題：

1.P是邊長為a的正三角形ABC所在平面外一點，且PA=PB=PC=a，則二面角P-AB-C的余弦值為_______.

2.已知P為銳二面角α-l-β的棱上一點，PQ?α，PQ與l成45°角，與β成30°角，則二面角α-l-β的大小為_______.

設計意圖：回顧二面角的計算的常用方法：1.定義法；2.三垂線定理法；3.垂面法.

學生獨立完成后，口頭回答結果，教師同學生一起反思解題過程，歸納方法及書寫格式，通過具體的問題，讓學生主動總結基礎知識和基本方法.

二、加強探究，培養學生的解題能力

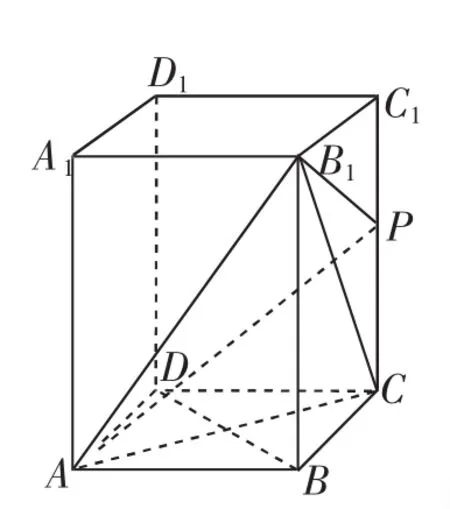
圖1

提高素質，培養能力是復習的重要目標，而能力的培養要通過學生的主動探究來實現.我們的做法是：根據教學內容、目標，精選示例，讓學生獨立思考或通過與同學合作討論解答，然后師生共同評價.

例1 如圖1，在正四棱柱ABCD-A1B1C1D1中，側棱長為2a，底面邊長為a，P是側棱CC1上一點.

（1）求證：BD⊥AP.

（2） 若CC1=3C1P，求平面AB1P與面ABCD所成的二面角.

讓學生獨立思考3分鐘左右，再口述思路.

生1：第一問用三垂線定理解決即可，第二問用射影法求解，但我沒有計算出來.

生3：可以用三垂線定理法，作出二面角的平面角，做法是：延長B1P與BC交點M點，再連接AM，然后過B作BH⊥AM于H，連接B1H即可，∠B1HB就是二面角的平面角.

師：講得很好，思路很正確.還有沒有其他方法呢？

生4：以D為坐標原點，分別以DA、DC、DD1為x、y、z軸建立空間直角坐標系.設底面邊長為3.易得平面ABCD和平面AB1P的法向量分別為n1=（0，0，1）、n2=（-1，3，1.5）.

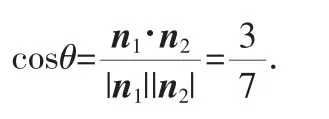
教師進行總結.

這樣，通過獨立思考，分組協作，互相交流，再通過師生共同解答過程進行反思、比較，使學生主動領悟、吸收、內化解題規律，訓練了思維的深刻性、靈活性，在學生主動探究學習的活動中，能力得到了提高，在整個復習過程中達到高考復習數學的總目標.