一道中國香港數學奧林匹克幾何賽題新證

●陳 宇 (姜堰中等專業學校 江蘇姜堰 225500)

第12屆中國香港數學奧林匹克試題第3題：

如圖1，在 Rt△ABC中，已知∠C=90°，作 CD⊥AB于點D.設O是△BCD外接圓的圓心，在△ACD內有一圓分別與線段AD，AC切于點M，N，并與⊙O 相切.證明：

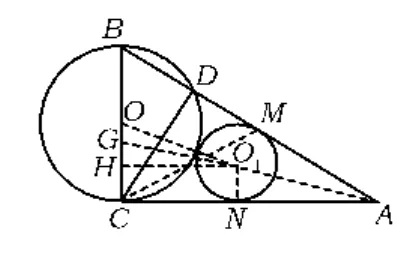
圖1

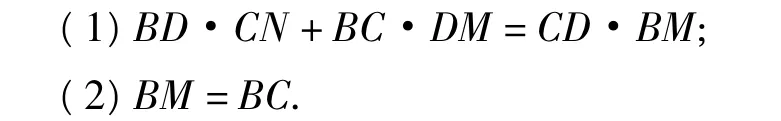
文獻［2］認為：文獻［1］提供的參考答案是從證明一個不容易想到的引理出發，然后利用托勒密定理加以解決，實屬不易.注意到問題(1)，(2)涉及的線段較多，為此文獻［2］依據圖形的結構特征，用解析法給出該題的一個另證.

經過一番探究，筆者發現，依據三角及代數計算可以給出該題的一個新證，且思路及計算也頗為簡潔.

證明(1)設∠BAC=2α(0°＜ α ＜45°)，BC=2a，圓 Γ1的圓心為 O1，半徑為 b.由題設知：∠BAC=∠BCD，AM=AN，OB=OC=a且0＜b＜a.分別聯結 OO1，O1N，則

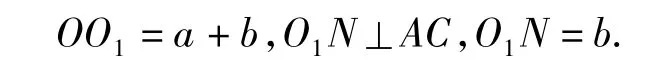
聯結AO1并延長交BC于點G，則AG平分∠BAC(易知 CG＜CO＜GB).過點O1作 O1H⊥BC于點H，則

［1］ 中等數學編輯部.2009-2010國內外數學競賽題及精解［J］.中等數學，2011(增刊)：25-26.

［2］ 彭成.一道中國香港數學奧林匹克幾何題的另證［J］.數學通訊，2012(6)：64.