廣義經驗似然估計量的結構參數檢驗水平校正

李 昊

0 前言

Hansen(1982)的廣義矩方法（GMM）已成為應用經濟計量研究的重要框架。然而，隨著應用的推廣和理論研究的深入，大量文獻表明（如Stock等(2002)的綜述），當工具變量與模型的內生變量弱相關或出現弱工具現象時，Hansen(1982)的廣義矩方法（GMM）及兩階段最小二乘法所使用的兩步估計程序將出現結構參數的不準確估計及評估估計結果的標準檢驗的不可靠推斷。

在GMM框架下，弱工具問題源于工具變量與模型蘊含的矩條件弱相關，Stock和Wright(2000)證明，弱工具下GMM估計量的極限分布不再是正態分布，且極限分布中包含結構方程擾動項，即擾人參數。他們建議使用Anderson和Rubin(1949)提出的對工具變量穩健的AR統計量實行結構參數檢驗。AR統計量將結構方程的擾動項投影到全體工具，極限分布是卡方分布，自由度參數是工具變量個數。但是，當工具的數目遠遠大于結構參數個數時，AR統計量功效很低。Kleibergen(2002)在AR統計量基礎上發展出K統計量來彌補此不足。和AR統計量類似，K統計量漸近服從卡方分布且獨立于擾人參數。不同于AR統計量，K統計量把結構方程的擾動項投影到屬于結構參數的內生變量工具估計。K統計量的優點表現為不論工具的質量如何及工具的個數有多少，這個估計漸近獨立于結構方程擾動項，極限分布的自由度參數等于全體結構參數個數。由于K統計量的極限分布不再依賴于所使用的工具個數，它可以比較使用不同工具個數下的結構參數估計結果。Kleibergen(2002)表明，K統計量是集中對數似然得分的二次型，而有限信息極大似然估計量恰好令這個得分為零。因此，K統計量的最小值將在有限信息極大似然處取得且等于零。該性質保證了K統計量的置信集非空且在每個顯著性水平上涵括有限信息極大似然估計。然而，這一性質也意味著K統計量不能區分目標函數的最小值、最大值和拐點，因為它將在這三個點處取值為零。特別地，在拐點處取值為零意味著模型矩條件沒有被滿足，此時K統計量的結論是偽結論。

我國的實證研究經常面臨的一個困境是樣本數據長度不足。而對于可利用的小樣本，又必須依據極限分布理論來進行結構參數的假設檢驗。面板數據模型是解決樣本數據長度的一個實用方法。但是，面板數據模型下K統計量是否能為我們所利用？它的小樣本性質是否會發生變化？這些問題尚未得到充分揭示。為此，本文將首先回顧結構參數穩健檢驗的發展，提出用廣義經驗似然估計量蘊含的經驗概率加權來獲取矩條件協方差估計，基于此來校正結構參數檢驗的水平扭曲，從而使有限樣本下的結構參數檢驗可以產生穩健的結論。

1 結構參數穩健檢驗

考察線性工具變量模型

其中Y是n×1維因變量向量，X是n×k維獨立變量矩陣，Z是n×m維工具變量矩陣，m≥k。ε和υ是誤差向量，β和π是未知參數。假定滿足模型的參數β具有唯一真值β0，正交矩條件是

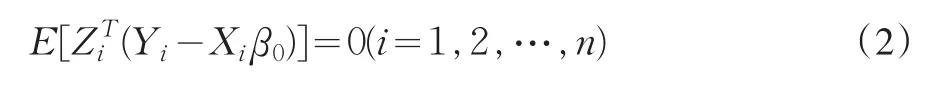
Stock等(2002)指出，如果π=0，工具是無效工具；如果π有固定的全秩，工具是有效工具；如果π與某個m×k維固定全秩矩陣成比例，工具是弱工具。

模型的傳統估計方法是兩階段最小二乘(2SLS)或廣義矩方法(GMM)。然而，當工具是弱工具時，它們的模型參數估計及檢驗存在如下問題：點估計量有偏，置信區間不準確，檢驗統計量水平扭曲。Bound等(1995)表明，這些問題不僅僅是小樣本問題，當樣本多達329000個觀測時，弱工具導致的分析結論非可靠的問題仍然存在。因此，一個自然的想法是尋找判別強工具的準則。Stock等(2002)提出了一個經驗法則：如果模型的聯合F統計量足夠大，可以認為使用的工具是強工具。他們建議的足夠大標準是10。但是，經驗法則并非一個判別工具強弱的充分條件，并且該法則僅適用于一個內生變量的模型，而實踐中研究者經常面臨的是多個內生變量。經驗法則的局限性推動了文獻從點估計朝向區間估計發展以使用弱工具穩健檢驗的研究。

文獻中弱工具穩健檢驗主要有三種，分別是Anderson和Rubin(1949)的AR檢驗，Kleibergen(2002)的K檢驗和Moreira(2003)的M檢驗。Moreira(2009)表明，這三個檢驗是下面兩個充分統計量的不同組合

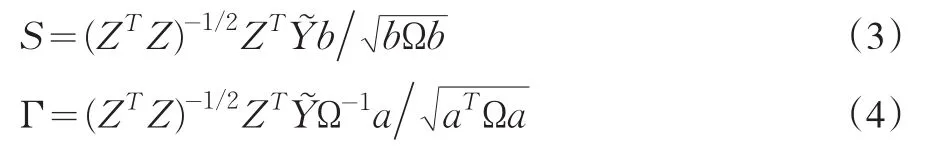
式（5）服從自由度等于結構參數個數k的卡方分布。K統計量是集中對數似然得分的二次型，而有限信息極大似然估計量恰好是令這個得分為零。因此，K統計量的最小值將在有限信息極大似然處取得且等于零。該性質保證了K統計量的置信集非空且在每個顯著性水平上涵括有限信息極大似然估計。然而，這一性質也意味著K統計量不能區分目標函數的最小值、最大值和拐點，因為它將在這三個點處取值為零。特別地，在拐點處取值為零意味著模型矩條件沒有被滿足，此時K統計量的結論是偽結論。

Kleibergen(2005)提出了K統計量的廣義矩拉朗日乘子形式來解決K統計量對拐點的取偽問題，本文稱之為GMMK統計量。該統計量的基礎是Hansen等(1996)連續更新估計量的目標函數

其中

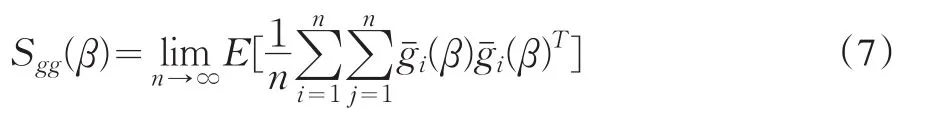
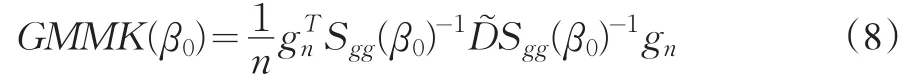
其中

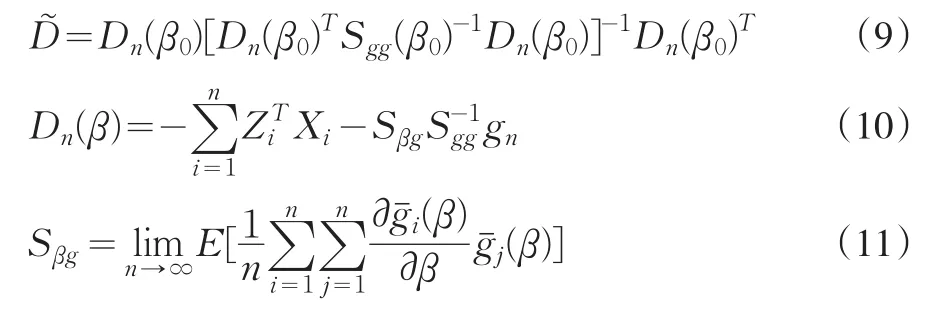
GMMK統計量（8）是不可行統計量，因為我們不知道矩方差（7），及矩條件和它的一階導函數的方差（11）。為使GMMK統計量可行，需要獲取它們的一致估計量以替代未知的矩方差。一個最簡單的形式是

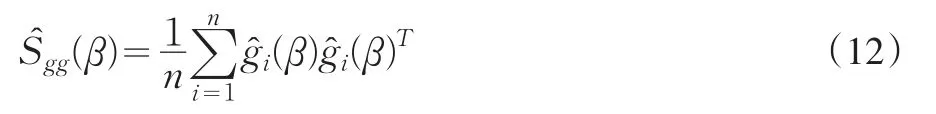
和

其中

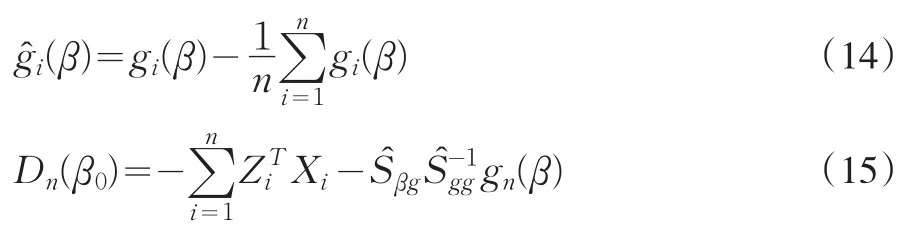
2 廣義經驗似然估計量

Owen(1988)首次使用似然函數來度量經驗分布和模型潛在的分布之間的離散距離，即經驗似然方法。如果模型正確識別，Owen(2001)表明經驗似然方法結合矩條件估計模型時擁有一致漸近正態的優良性質。Qin和Lawless(1994)在獨立同分布條件下推導出經驗似然估計量（EL），Kitamura(1997)將其推廣到弱相依過程。對給定的樣本規模n和觀測數據 zi(i=1,2,…,n)，樣本的離散概率(p1,p2,…,pn)的經驗似然是

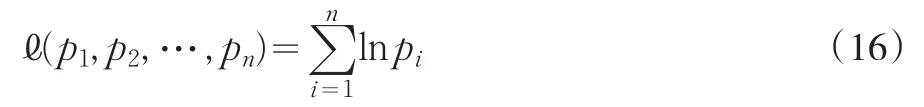
并結合矩函數g(zi,θ)建立下面的約束條件

求解最優化問題(17)式即可得到經驗似然估計量。從約束條件(18)式可以看出，經驗似然估計量考慮了有限樣本分布中樣本點具有不同的經驗分布概率pi的可能（pi是參數θ的函數）。經驗似然估計量及以它為基礎發展的估計量關注于有限樣本下樣本矩的不同概率加權，而傳統的廣義矩估計量考察的是等概率加權的樣本矩

對應 pi=1/n時，式(16)達到最大值-nlogn的情形。這表明GMM隱含地規定有限樣本下樣本點經驗概率等于，即服從均勻分布，而EL視經驗概率服從多元聯合分布π=(p1,p2,…,pn)。這一點上的差異構成GMM和GEL的主要差異。

經驗似然約束最優化問題的拉格朗日函數是

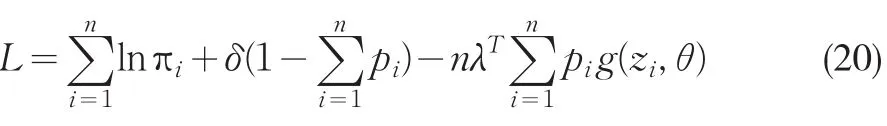
其中λ是拉氏乘子，用迭代算法求解λ

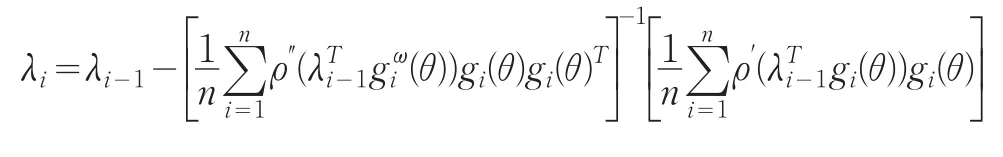
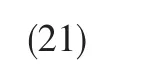
可解得經驗概率

和參數θ0的經驗似然估計量

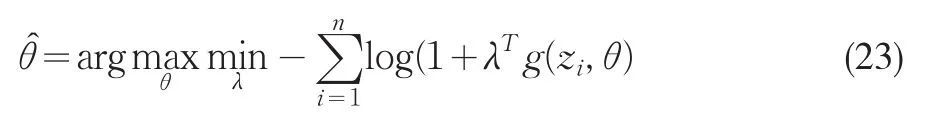
Qin和Lawless(1994)推導了經驗似然估計量(23)的漸近分布。令 G=E[?θg(z,θ0)]，S=E[g(z,θ0)g( )z,θ0T]，那么

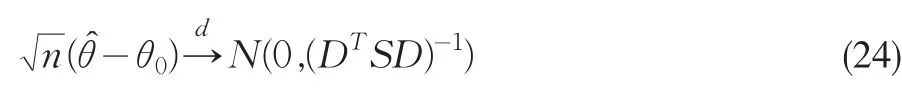
Imbens(1997)和Smith(1997)在Qin和Lawless(1994)的基礎上提出指數加權估計量(ET)，它的目標函數是

Imbens等(1998)證明，如果使用Cressie-Read離散準則作目標函數，EL和ET同屬一類估計量，他們稱之為廣義經驗似然估計量。Cressie-Read冪離散準則是

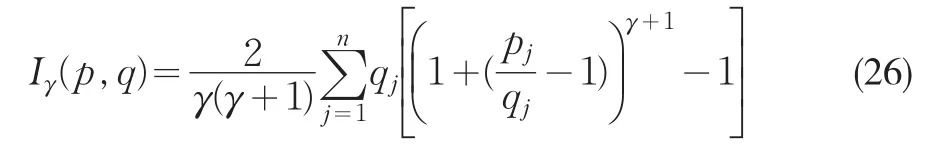
p和q是不同的概率測度集。Smith(1997)證明Owen(2001)的EL對應γ=0，Kitamura和Stutzer(1997)的ET對應γ=-1。Newey和Smith(2004)證明Hansen等(1996)的連續更新估計量對應 γ=1。Kitamura和Stutzer(1997)指出在求解前預先平滑觀測值可使EL和ET達到與GMM相同的漸近協方差。Newey和Smith(2004)表明Hansen(1996)的連續更新估計量是廣義經驗似然估計量的特例，在獨立同分布條件下推導了廣義經驗似然估計量的高階性質，證明GEL相比GMM具有更小的高階偏差。

Newey和Smith(2004)將廣義經驗似然類估計量歸結為奇點問題(27)式的解

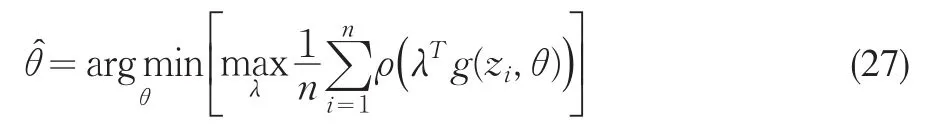
其中λ是約束最優化問題的拉氏乘子。dn(pt)度量 pt與1/ n的距離，屬于Cressie-Read函數。ρ(?)是標準化后的嚴格凸函數，依據不同的Cressie-Read函數族參數γ對應不同的廣義經驗似然類估計量。如果令υ=λTgω(zi,θ)，那么經驗似然估計量(EL)對應 ρ(υ)=ln(1-υ)，指數加權估計量（ET）對應ρ(υ)=-exp(υ)，連續更新估計量（CU）對應 υ的二次型。我們可以分別寫出這三個估計量的目標函數如下

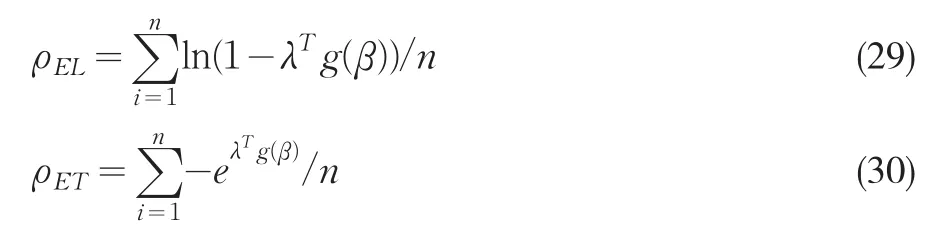
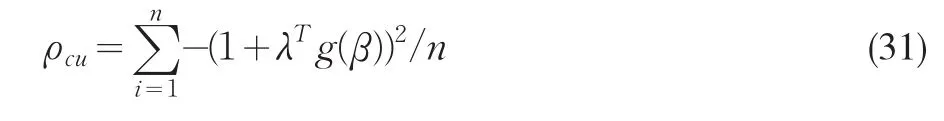
3 穩健檢驗的廣義經驗似然備擇

不同于GMMK統計量基于GMM的目標函數，GELK檢驗基于GEL的目標函數。發展GELK檢驗的目的是期望GEL程序能探測出樣本數據中的異常值并對異常值賦予相對小的權重。由于GMM程序賦予全體樣本觀測值以等概率權重，我們期望GELK檢驗從理論上來說會表現得比GMMK檢驗要好。

Guggenberger和Smith(2005)推導了Wald類和LM類的GEL基礎的K檢驗，基本思想是通過計算GEL目標函數的一階導數并在原假設處估值。

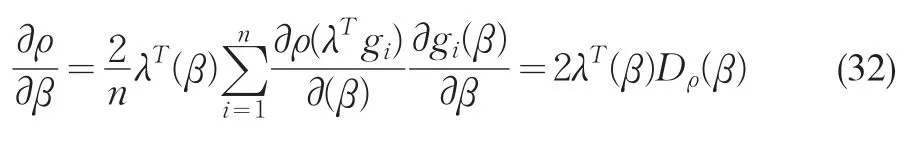
式（32）中的Dρ表示GEL類目標函數的導數。對于線性工具變量模型，我們有

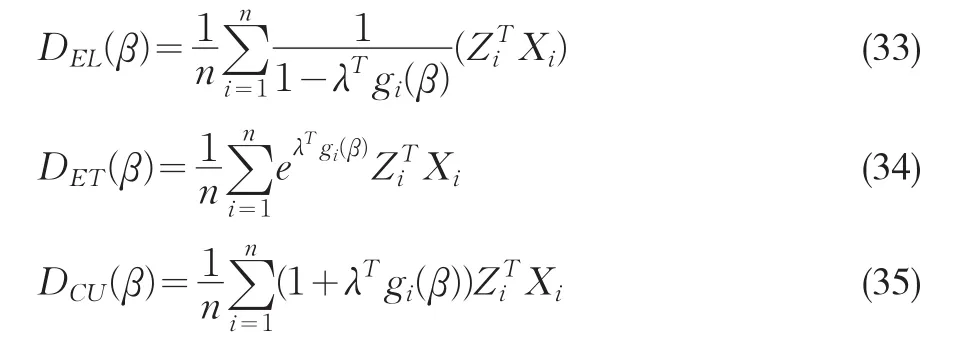
Guggenberger和Smith給出GELK的表達式

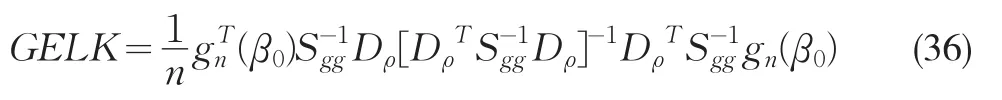
Guggenberger和Smith(2005)考察了線性聯立方程的GELK檢驗。筆者注意到，他們忽略了可以利用GEL估計量所對應的概率去重新加權矩條件協方差以改善矩條件協方差估計。使用GEL估計的概率去再加權矩條件協方差矩陣估計量

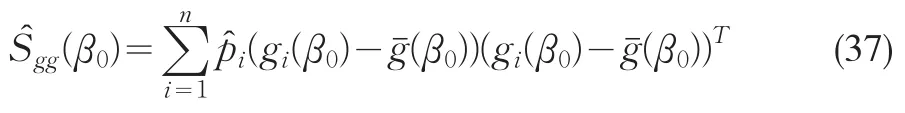
其中 ρ1(?)是 GEL 目標函數 ρ(?) 的一階導函數，它的不同形式對應式(29)～(31)。

4 仿真實驗

為檢驗矩條件協方差概率加權對GELK檢驗的改善效果，本文使用一個簡單的固定效應動態面板AR(1)模型

其中T相對N很小：i=1,2,…,N；t=1,2,…,T；?∈(0,1)。 αi～N(0,σα)，表示各截面的固定效應。 εit跨截面N和時序T獨立，均值為0，方差為σ2ε。為消除固定效應，對方程進行一階差分得

其中 Δ 是差分算子，如 Δyit=yit-yi,t-1。由于Δyi,t-1=yit-1-yit-2和 Δεit=εit-εit-1會因 yi,t-1和 εi,t-1的相關而相關，所以方程(40)的普通最小二乘估計將有偏。傳統上使用工具變量消除Δyi,t-1和Δεi,t的相關，如二階段最小二乘和廣義矩方法。方程的工具變量選取一般是 yit的二階滯后項，如yi,t-2。顯而易見，yi,t-2與Δyi,t-1相關，與 Δεi,t不相關，因此 yi,t-2是 Δyi,t-1的有效工具變量。

按照Arellano和Bond(1991)的思路，我們可以取yit的二階滯后或更高階滯后作工具，每個截面i的工具矩陣可表達為

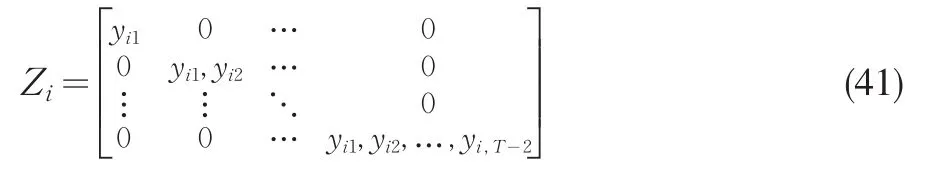
然而，Stock等(2002)表明模型(40)的所使用的工具矩陣(41)的強度依賴于未知參數?。當?接近1，工具是弱工具，且基于二階段最小二乘的標準Wald檢驗過度拒絕原假設，有嚴重的水平扭曲現象。因而Stock等(2002)建議使用Anderson和Rubin(1949)的AR統計量進行結構參數檢驗。雖然AR統計量對弱工具具有穩健性，但它的極限分布依賴于工具變量個數。Arellano和Bond(1991)的動態面板估計方法表明，可以使用yit的滯后二階或更高階作模型(40)的工具。因此，Kleibergen(2002)在AR統計量基礎上發展K統計量，它的極限分布僅依賴于結構參數個數。

本文使用模型(39)進行蒙特卡羅仿真試驗。固定效應αi服從正態分布，均值為零，方差取2(1-?)2。結構參數?的取值是(0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9)。為模擬誤差項的有限分布性質，從t分布中抽取誤差項，自由度為10。t分布的峰度是6/(υ-4)（υ是自由度），所以取υ=10能較好地模擬有限樣本分布中常出現的尾部概率。為確保初值不為零，令初值 yi0=αi+εi0，εi0從標準正態分布中抽取。本文的仿真試驗分別設定截面N=50,80,100；設定時序T=6,8,10；設定工具滯后L=2,3,4。L代表工具滯后階數，等于2表示僅用到滯后二階；等于3表示用到yit的滯后二階和三階作為工具。試驗取名義顯著性水平0.05，每次模擬生成1000個樣本來考察五個檢驗統計量的實際顯著性水平：GMM，EL,ET,CU和Wald。依據N，T，L不同的取值組合，試驗考察了7種情況，結果展示在圖1～7

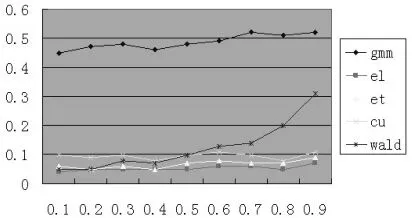
圖1 N＝50，T＝8，L＝2

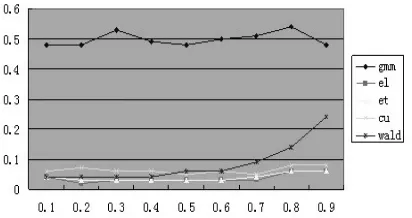
圖2 N＝80，T＝8，L＝2

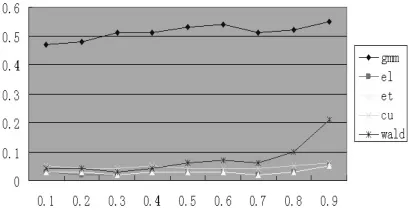
圖3 N＝100，T＝8，L＝2

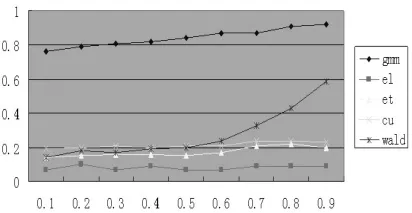
圖4 N＝50，T＝8，L＝3

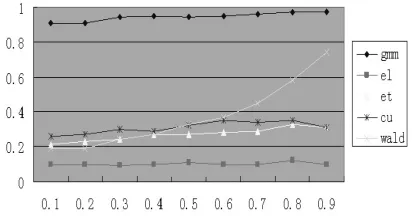
圖5 N＝50，T＝8，L＝4

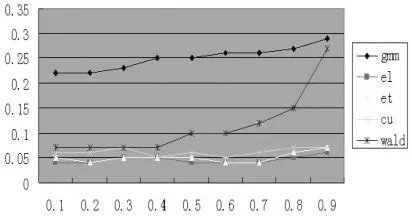
圖6 N＝50，T＝6，L＝2

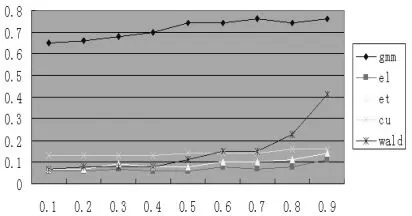
圖7 N＝50，T＝10，L＝2

首先，我們展示了基于GELK檢驗統計量、對矩條件協方差矩陣經驗概率加權后的改善效果。圖6～7可以發現EL的表現最好，拒絕原假設的比例在0.1左右；GMM的表現最差,拒絕原假設的比例超過了0.5。因此，仿真試驗結果表明EL檢驗統計量的顯著性水平改善最佳，證明了基于廣義經驗似然估計量以經驗概率加權能有效地改善K檢驗。全體結果還表明，當?趨近于1時，Wald檢驗統計量傾向于過度拒絕原假設，這符合Stock(2002)的結論。

其次，我們還展示了截面、時序和工具滯后階三個參數不同取值對全體檢驗統計量的影響。圖1～3給出了截面變動時各統計量的表現，圖4～5給出工具滯后階數變動時各統計量的表現，圖6～7給出時序變動時各統計量的表現?？疾靾D1～3可以發現，當截面數目增加時，所有估計量的過度拒絕現象都有改善，檢驗的真實顯著性水平收斂于名義顯著性水平5%。圖4～5表明，工具滯后階數的增加對不同的檢驗統計量有不同影響后果，EL檢驗的真實顯著性水平較穩定，傳統的Wald檢驗過度拒絕現象加劇，ET和CU的真實顯著性水平隨著?值的增加而快速增加。這表明使用過多的滯后階數作工具并不能達到預期的效果。圖6～7表明對固定的N，中等大小的時序將使得檢驗統計量具有較好的表現效果。

5 結論

本文改善廣義經驗似然Kleibergen類結構參數檢驗，基本思路是以廣義經驗似然類估計量伴隨的經驗概率來加權矩條件協方差估計。本文設計并實現了動態面板模型的蒙特卡羅實驗，結果表明，在有限樣本特別是小樣本的條件下，傳統的基于廣義矩估計量的結構參數檢驗存在嚴重的水平扭曲。這一結論說明，在廣義矩框架下，若對結構參數的約束基于Wald統計量的極限分布來進行檢驗，很可能產生錯誤的結論。進一步，本文使用經驗概率加權獲得了比等概率1 /n加權更好的檢驗結果。這一結論強烈推薦，在對結構參數進行假設檢驗時，為保證結構的穩健性，應使用廣義經驗似然估計量并基于此產生檢驗結論。

本文使用動態面板模型評價結構參數檢驗的有限樣本表現，一是面板數據模型在學術界廣為研究和應用，二是因為面板數據模型的估計嚴重依賴于工具變量的質量和未知待估關注參數的真實值。本文研究發現，在5%名義顯著性水平下，經驗似然檢驗統計量基礎的檢驗表現最好，基于廣義矩檢驗統計量的檢驗水平扭曲嚴重。實際應用中，我們往往不知道研究模型的真實的結構參數，并且還不得不依賴工具變量方法展開參數估計。因而，對工具變量的質量和參數的真實值的檢驗是否穩健直接影響著實證研究后續結論的可靠性。基于全文的研究，我們建議使用經驗似然檢驗估計量對結構參數進行穩健檢驗；特別地，經驗似然概率加權擁有相對其他備擇方法的最佳表現。

[1] Anderson,T.Rubin,H.,Estimation of the Parameters of a Single Equa?tion in a Complete Set of Stochastic Equations[J].The Annals of Mathe?matical Statistics,1949,(21).

[2] Arellano,M.,Bond,S.Some Tests of Specification for Panel Data:Mon?te Carlo Evidence and an Application to Employment Equations[J].The Review of Economic Studies,1991,(58).

[3] Bound,J.Jaeger,D.A.,Baker,R.M.Problem with Instrumental Vari?ables Estimation when the Correlation between the Instruments and the Endogenous Explanatory Variables is Weak[J].Journal of the American Statistical Associations,1995,(90).

[4] Guggenberger,P.,Smith,R.J.Generalized Empirical Likelihood Esti?mators and Tests under Partial,Weak,and Strong Identification[J].Econometric Theory,2005,(21).

[5] Hansen,L.P.Large Sample of Generalized Method of Moments Esti?mators[J].Econometrica,1982,(50).

[6] Hansen,L.P.,Heaton,J.,Yaron,A.Finite-Sample Properties of Some Alternative GMM Estimators[J].Journal of Business&Economic Sta?tistics,1996,(14).

[7] Imbens,G.One-Step Estimators for Over-Identified Generalized Method of Moments Models[J].Review of Economics Studies,1997,(64).

[8] Imbens,G.W.,Spady,R.H.,Johnson,P.Information Theoretic Ap?proaches to Inference in Moment Condition Models[J].Econometrica,1998,(66).

[9] Kitamura,Y.,Stutzer,M.An Information-Theoretic Alternative to Gen?eralized Method of Moments Estimation[J].Econometrica,1997,(65).

[10] Kleibergen,F.Testing Parameters in GMM without Assuming that they are Identified[J].Econometrica,2005,(73).

[11] Kleibergen,F.Pivotal Statistics For Testing Structural Parameters In Instrumental Variables Regression[J].Econometrica,2002,(70).

[12] Moreira,M.J.Tests with Correct Size when Instruments Can be Arbi?trarily Weak[J].Journal of Econometrics,2009,152(2).

[13] Newey,W.K.,Smith,R.J.Higher Order Properties of GMMandGen?eralized EmpiricalLikelihood Estimators[J].Econometrica,2004,(72).