錐度量空間中擴張映射的一個新的不動點定理
史曉棠,谷峰
(杭州師范大學理學院,浙江杭州 310036)
錐度量空間中擴張映射的一個新的不動點定理
史曉棠,谷峰
(杭州師范大學理學院,浙江杭州 310036)
為了研究完備的錐度量空間中擴張型映象不動點的存在性和唯一性問題,對滿足不同條件的擴張型映象,采用不同的迭代方法,得到了錐度量空間中擴張映射的一個新的不動點定理.這些結果是度量空間中某些經典結果在錐度量空間的進一步推廣和發展.
錐度量空間;擴張映射;不動點
1 引言
眾所周知,非線性算子不動點的存在性及唯一性研究是非線性分析的重要研究課題之一,而且不動點理論廣泛的應用于非線性積分方程和微分方程中[16].擴張型映射是一類重要的非線性映射,關于這類映射不動點的存在性的研究同樣備受人們關注.目前,在錐度量空間中有關擴張型映射的不動點的結果微乎其微.文獻[7]引進了錐度量空間并且在完備的錐度量空間中證明了Banach壓縮映象原理依然成立.隨后,文獻[8]推廣了文獻[7]的結果.最近,文獻[9-18]在錐度量空間中研究了滿足一定壓縮條件的非線性算子的不動點的存在性問題,得到了一些新結果.本文主要在完備錐度量空間中研究擴張型映射不動點存在性問題,得到了幾個新的不動點定理,本文的結果推廣了一些已知的相關結果,而且也是度量空間中某些經典結果在錐度量空間的進一步推廣.
在介紹主要結果之前,先介紹一些基本概念和已知結果.
定義1.1設E是一個實Banach空間.P是E中的一個子集,稱P是一個錐,如果
(a)P是非空閉凸集且P/={θ},其中θ是E的零元素:
(b)若λ≥0且x∈P,則λx∈P;
(c)x∈P且-x∈P,則x=θ.
設P是E中的錐,由P所定義的半序“≤”如下:若y-x∈P,則x≤y.用x?y表示y-x∈int P(P的內點集).
定義1.2錐P稱為是正規的,若存在常數K>0,使當θ≤x≤y時,恒有‖x‖≤K‖y‖.
定義1.3錐P稱為是正則的,如果X中的每一個遞增(遞減)序列{xn}都有上(下)界,使得

則存在x∈E使‖xn-x‖→0(n→∞).
顯然,每個正則錐都是正規錐.
定義1.4令X是一個非空集.如果映射d:X×X→E滿足
(1)θ≤d(x,y)對一切x,y∈X.d(x,y)=θ當且僅當x=y;
(2)d(x,y)=d(y,x),?x,y∈X;
(3)d(x,y)≤d(x,z)+d(z,y),?x,y,z∈X.
則稱d是X的一個錐度量.而(X,d)稱為錐度量空間,它是一般錐度量空間的推廣.
令(X,d)是一個錐度量空間,{xn}?X.
(4)稱{xn}是一個柯西列,若對每一個c∈E且c?θ,存在正整數N使得對所有的n,m>N有d(xn,xm)?c;
(5)稱{xn}是一個收斂列,若對每一個c∈E且c?θ,存在正整數N使得對所有的n>N有d(xn,x)?c,其中x∈X,稱x是{xn}的極限,記作
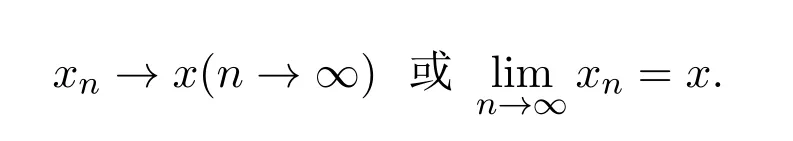
錐度量空間(X,d)稱為完備的是指對X中的每一個柯西列都在X中收斂.
引理1.1設(X,d)是錐度量空間,E是Banach空間,P?E是錐,int P/=?.設{xn}與{yn}是X中的兩個序列,且xn→x0,yn→y0(n→∞).則
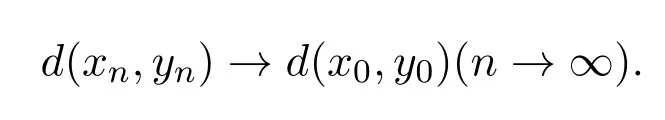
證明因為xn→x0,yn→y0(n→∞),所以對任意的c∈E,c?0,存在正整數N,使當n>N時,有

由三角不等式可得:

于是,當n>N時,有
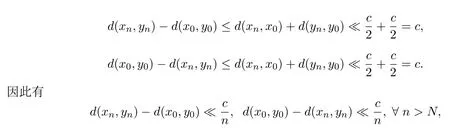

2 主要結果


即Tx*也是Tp,Tq的公共不動點.由x*的唯一性得Tx*=x*,因此x*是T的唯一不動點.
推論2.1設(X,d)是一個完備的錐度量空間,P是E中的正則錐.映射T:X→X是滿射并且滿足:其中a(t):E+→(1,∞)是單調遞增函數,則T在X中存在唯一不動點.

證明在定理2.1中,令p=q=1即可.
定理2.2設(X,d)是一個完備的錐度量空間,P是E中的正則錐.映射T:X→X是滿射并且滿足:

其中p,q∈?+,a(t),b(t),c(t):E+→[0,∞)是單調遞增函數,并且滿足a(t)+b(t)+c(t)>1.如果0<a(t)/=1,則T在X中存在唯一不動點.
證明類似于定理2.1,可取點列:

對任意的n∈?+,不妨設y2n-1/=y2n且y2n/=y2n+1.這是因為,如果對某個自然數n有y2n-1=y2n,則由y2n-1=Tpy2n知y2n=Tpy2n,于是由(9)式可得:
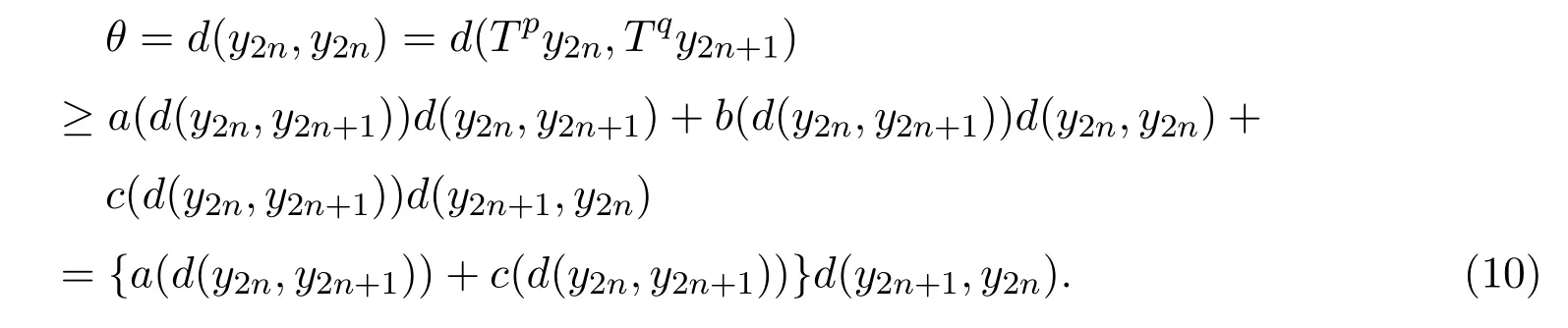
因為a(t)+c(t)≥a(t)>0,從而由上式得y2n=y2n+1.又y2n=Tqy2n+1,所以y2n=Tqy2n,因此y2n是Tp,Tq的公共不動點.若還有z∈X也是Tp,Tq的公共不動點,則由條件(9)式有

因0<a(t)/=1,所以上式僅當y2n=z時成立.故y2n是Tp,Tq的唯一公共不動點.另外,顯然有Ty2n=Tp(Ty2n),Ty2n=Tq(Ty2n).即Ty2n也是Tp,Tq的公共不動點,由公共不動點的唯一性知,y2n=Ty2n,即y2n是T的唯一不動點.
同理,若y2n=y2n+1,則y2n+1就是T的唯一不動點.故不失一般性,可設y2n-1/=y2n且y2n/=y2n+1,于是就有



[1]Guo D J,Lakshm ikantham V.Coup led fixed point of nonlinear operators with app lications[J].Nonlinear Anal.,1987,11(5):623-632.
[2]Guo D J,Lakshm ikantham V.Nonlinear Problem s in Abstract Cone[M].New York:Academ ic Press,1988.
[3]Sun Y.A fixed point theorem s for m ixed monotone operators with app lications[J].J.Math.Anal.App l., 1991,156:240-246.
[4]Guo D J.Existence and uniqueness of positive fixed point form ixed monotone operators and app lications[J]. App l.Anal.,1992,46:91-100.
[5]Rhoades B E.Som e theorem s on weak ly contractivem appings[J].Non linear Anal.,2001,47:2683-2693.
[6]尹建東,鄧中書.幾個非線性算子不動點的存在性定理及其應用[J].南昌大學學報:理科版,2009,33(6):518-522.
[7]Huang L D,Zhang X.Cone m etric spaces and fixed point theorem s of contractive mappings[J].J.Math. Anal.App li.,2007,332:1468-1476.
[8]Abbas M,Rhoades B E.Fixed and periodic point results in cone m etric spaces[J].App l.Math.Letter., 2009,22:511-515.
[9]Abbas M,Jungck B G.Comm on fixed point results for noncommuting m appingswithout continuty in cone metric spaces[J].J.Math.Anal.App l.,2008,341:416-420.
[10]Yuan Q,Qin X.Fixed point theorem s for generalized contractions in cone m etric spaces[J].International Journal of Modern Mathematics,2009,4(3):269-275.
[11]張憲.錐度量空間中Lipschitz型映射的公共不動點定理[J].數學學報,2010,53(6):1319-1148.
[12]張石生.不動點理論及應用[M].重慶:重慶出版社,1984.
[13]楊云蘇,尹建東,廖川榮.錐度量空間中擴張映射的不動點定理[J].南昌大學學報:理科版,2010,34(2):117-119.
[14]Rezapour Sh,Ham lbarani R.Som e note on the paper“cone m etric space and fixed point theorem s of contractivemappings”[J]J.Math.Anal.App l.,2008,345:719-724.
[15]Tomonari Suzuki.A new type of fixed point theorem in m etric spaces[J].Nonlinear Analysis,2009,71:5313-5317.
[16]Abbas M,Rhoades B E,Nazir T.Comm on fixed points for four m aps in cone m etric spaces[J].App lied Mathematics and Com putation,2010,216:80-86.
[17]Binayak S,Choudhury,Metiya N.Fixed points of weak contractions in cone m etric spaces[J].Nonlinear Analysis,2010,72:1589-1593.
[18]Erdal Karapinar.Coup le fixed point theorem s for non linear contractions in conem etric spaces[J].Com puters and Mathem atics with App lications,2010,59:3656-3668.
A new fixed point theorem of expanding mappings in cone metric spaces
Shi Xiaotang,Gu Feng
(Institute of App lied Mathematics and Department of Mathematics,Hangzhou Normal University, Hangzhou 310036,China)
In order to investigate the fixed points for expandingm appings in com p lete conem etric cone spaces, different iterativemethods used for satisfying different expanding conditions,and several new results are gotten. The resu lts in this paper generalize a few known results.
conem etric space,expanding m appings,fixed point
O177.91
A
1008-5513(2012)03-0349-08
2011-01-08.
國家自然科學基金(11071169);浙江省自然科學基金(Y 6110287);杭州師范大學研究生教改基金.
史曉棠(1984-),碩士,研究方向:非線性泛函分析.
2010 MSC:47H10,54H25

