長白山主要樹種直徑生長的多元回歸預測模型:以云杉為例1)

劉 洋 亢新剛 郭艷榮 高北延 馮啟祥

(省部共建森林培育與保護教育部重點實驗室(北京林業大學)，北京，100083)(北京林業大學) (吉林省汪清林業局)

林分內各種大小直徑的樹木的分配狀態，直接影響樹木的樹高、干形、材積、材種及樹冠等因子的變化;林木直徑可以被快速、方便且準確地測量，同時它是許多森林經營技術及測樹制表技術理論的依據［1］。因此，直徑生長模型一直是單木模型的研究重點，它是一個或一組數學函數式，描述林木生長及林分狀態與立地條件、林分密度、周圍相鄰木距離、環境因子等變量之間的關系，并經一定方法處理后可預估林分直徑生長量、收獲量和林木枯損量。

直徑回歸方程是建立林分生長與收獲模型的基礎。國內外有關直徑預測模型也很多，大多數都是以經驗和理論生長方程為基礎擬合［2－7］，只考慮了林分密度，沒有考慮立地質量和對象木與相鄰木的最近距離對林木直徑生長的影響，多數都涉及的是與距離無關的林分的單木模型。筆者利用3個競爭指數反映立地質量、林分密度和對象木與相鄰木的最近距離，對直徑潛在生長函數進行修正，從而合理預測林木的未來直徑大小，為林分直徑生長模型提供一種新的途徑。

1 研究區概況

研究區位于吉林省汪清林業局金溝嶺林場，地理位置 130°10＇E，43°22＇N。地貌屬低山丘陵，海拔為300～1 200 m，坡度多在5°～25°。該區屬季風型氣候，全年平均氣溫3.9℃左右，積溫2 144℃，年降水量600～700 mm，生長期為120 d。土壤多為針葉林灰棕壤，溝谷是草甸土、泥炭土、沼澤土或沖積土，結構一般為黏壤土類，粒狀結構，濕松，根系多，平均厚度在40 cm左右。研究區為天然針闊葉混交過伐林。主要樹種有:云杉(Picea koraiensis)、冷杉(Abies nephrolepis)、紅松(Pinus koraiensis)、楓樺(Betula costata)、椴樹(Tilia amurensis)等，其它樹種還有:色木槭(Acer mono)、水曲柳(Fraxinus mandschurica)、胡桃楸(Juglans mandshurica)、黃菠蘿(Phellodendro namurense)、白樺(Betula platyphylla)、青楷槭(Acertegmentosum)、花楷槭(Acer ukurunduense)等。

2 材料和方法

2.1 數據資料

數據來源于1982—1988年在吉林省汪清林業局金溝嶺林場設立的26塊皆伐標準地的1381株云杉解析木和101株云杉標準木，26塊皆伐標準地林型基本一致，土壤類型均為棕色森林土。在數據分析時主要查閱了以下外業調查表。

土壤調查表:包括土壤種類、濕度以及土壤表面的枯落物厚度、腐殖質層厚度和土壤總厚度;

環境因子調查表:包括標準地位置的海拔高度、地形、坡位、坡度和坡向等因子;

每木調查表:記載了林分狀況及對象木與鄰近樹木的位置關系、胸徑、樹高、枝下高和冠幅。

在標準地外業調查表的基礎上，計算出皆伐標準地樹種組成、林分密度、斷面積、蓄積量等因子，具體情況見表1。

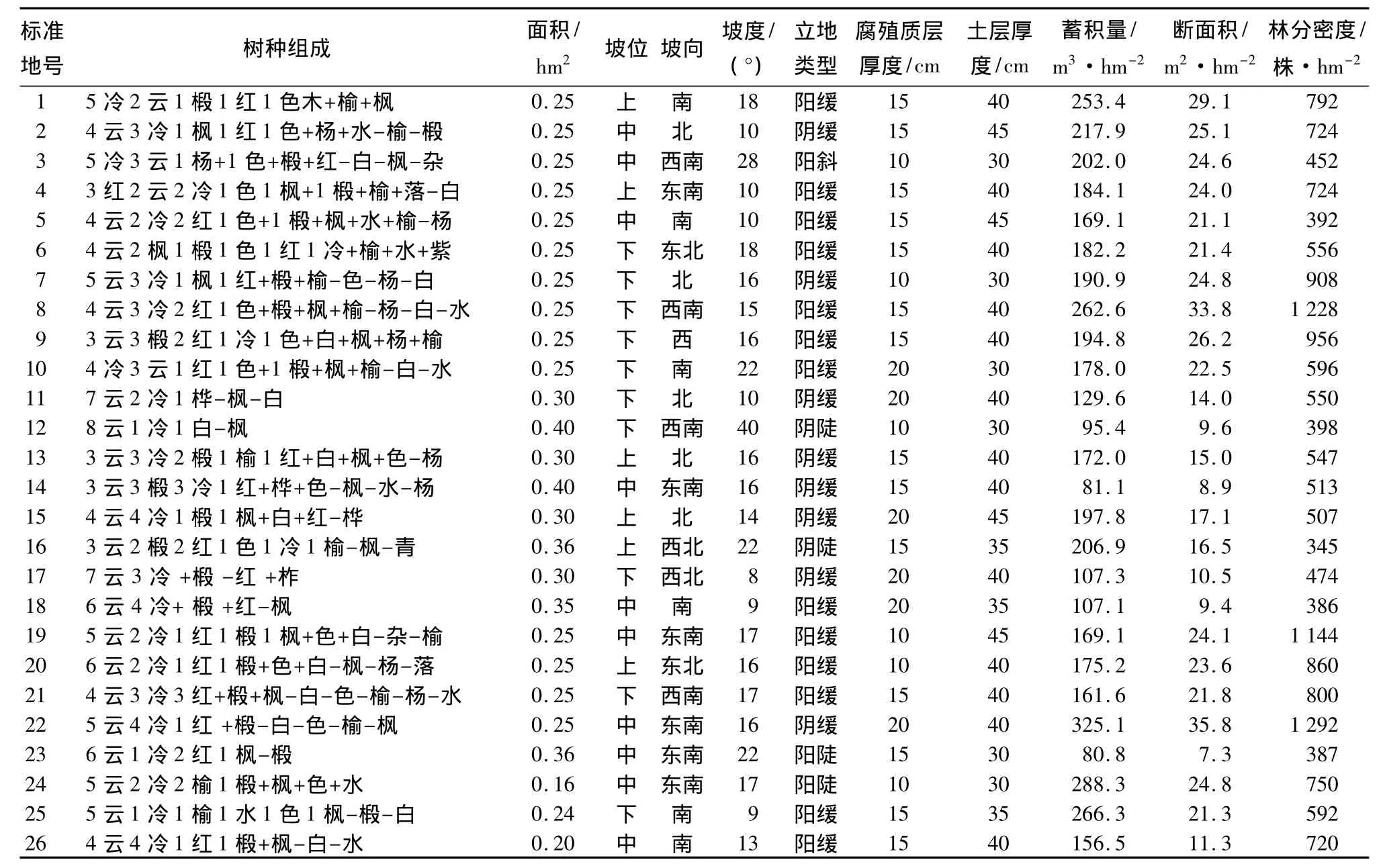
表1 長白山地區26塊皆伐標準地基本概況

2.2 研究方法

選用潛在生長量修正法建立林木直徑生長模型。模型用數式可表示為:

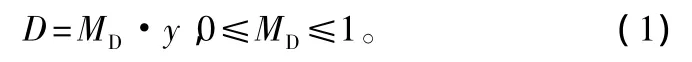
式中:D為林木直徑;MD為修正函數;y為潛在直徑生長函數。

由于林木間相互競爭，林分內絕大多數林木實際生長量小于潛在生長量，減小的程度與競爭程度有關［1］。從理論上來說，林木潛在生長函數應由疏開木的生長過程來確定。由于疏開木難以確定，有些研究者建議用相同年齡時優勢木的生長過程代替疏開木的生長過程［8］。本研究在生長模型建模中，假定環境條件一致的條件下，選取18塊皆伐標準地林分內的優勢木直徑，確定林木直徑的潛在生長量，以Richards方程建立了潛在直徑生長函數。然后用反映立地質量、林分密度、林木最近距離的3個競爭指數即地位級曲線方程、樹冠競爭因子和2參數的Weibull分布函數所表示的修正函數對直徑潛在生長函數進行修正。采用SPSS軟件對參數進行擬合，并依據相關系數最大，剩余平方和最小得到直徑實際生長的多元回歸預測模型。

3 結果與分析

3.1 潛在直徑生長函數的建立

樹木生長理論方程有Logistic方程、Mitscherlich方程、Richards方程，理論上可以證明Logistic方程和Mitscherlich方程均是Richards方程的特例，并且Richards方程是近代應用最為廣泛、適用性較強的一類生長曲線方程。因此，筆者以Richards方程為基礎，研建直徑的潛在生長量函數。Richards方程的形式為:

式中:y為優勢木的直徑;A為優勢木年齡;M、K、B為方程參數。

Richards方程中各參數的生物學意義:參數M為y的最終值即上漸近值，即給出生長因子最終達到值;參數B決定曲線形狀和拐點位置;參數K起著調節生長時間的作用，此值越大，生長時間便越短，它與生長速率是密切相關的［9］。

依據18塊皆伐標準地林分內的優勢木直徑和年齡，利用SPSS軟件對上述公式(2)進行擬合，得到M=55.253，K=0.018，B=2.389，R2=0.871。疏開木直徑潛在生長函數為:

3.2 地位級

林木胸徑的大小與立地質量有關。此外由于林分高也比較容易測定，與平均胸徑及蓄積量相比，受林分密度影響較小，所以地位級作為評價立地質量高低的依據為各國普遍采用。常用的擬合地位級的數學模型有:對數雙曲線式、對數曲線式、拋物線式、單分子式、理查茲式和雙曲線式等。

本研究選取研究區78株云杉標準木的樹高和年齡，采用SPSS軟件對地位級的上述6個數學模型進行擬合。6個曲線方程中，對數曲線式lg(H)=a+blg(A)的相關系數(R2=0.895)最大，且參數a=0.350，b=0.448。因此，地位級曲線方程為:

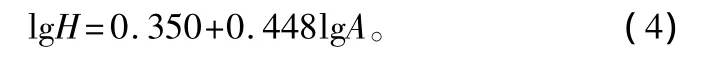
式中:H為林分平均高;A為林分年齡;a、b為待定參數。

3.3 林分密度

林分密度說明林木對其所有空間的利用程度，它是影響林分生長和木材數量、質量的重要因子。林分中林木間的擁擠程度取決于林分密度、林木平均大小以及林木在林地上的分布。自由樹的樹冠冠幅與樹木胸徑之間呈顯著的線性正相關，這種線性關系不隨樹木的年齡及立地條件的變化而改變，這正是利用樹冠反映林分密度的可靠依據。Krajicek等［10］利用這一關系提出了樹冠競爭因子(FCC)。(FCC)的具體確定方法如下:

①以疏開木的冠幅與胸徑間的相關關系為基礎，求出最大樹冠面積。設疏開木冠幅與胸徑的關系為:

式中:Cw為優勢木冠幅;D為優勢木胸徑;a、b為待定參數。

依據18塊皆伐標準地林分內的優勢木胸徑與冠幅，利用上述公式(5)進行擬合。擬合結果為:a=5.906，b=0.240，R2=0.884。即:

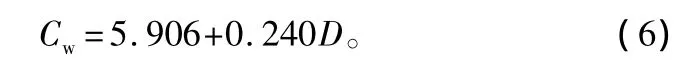
②對于胸徑為Di的林木最大樹冠面積應等于同胸徑的疏開木樹冠面積(AMC)i，即:

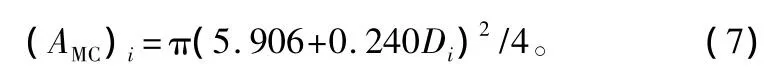
③將單位面積林分中每株樹木的最大樹冠面積相加即為該林分的樹冠競爭因子(FCC)。即:

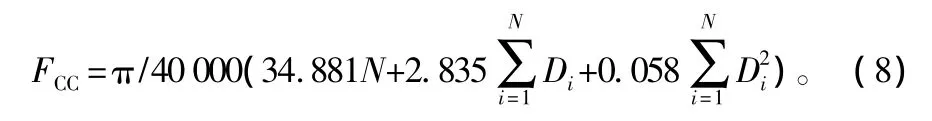
式中:Di為自由樹(林分中優勢木)胸徑;N為林分密度，由表1中查得。

3.4 林木最近距離的影響

林木的生長不僅取決于其自身的生長潛力，而且還取決于其與周圍競爭木的競爭能力。競爭能力的大小決定于競爭木與對象木之間的距離。根據文獻［11］，林木最近距離分布為單峰型，可用Weibull分布函數予以恰當描述。對于林木水平分布格局為團狀或隨機分布的森林群落(如結構豐富的天然林)而言，其林木最近距離分布僅用 2參數的Weibull分布函數(a=0)足以很好地表達;而對于林木水平分布格局為十分均勻的森林群落(如人工林)而言，其林木最近距離分布才需要用3參數的Weibull分布來描述。

本研究對象為天然林a=0，則2參數Weibull分布函數為:

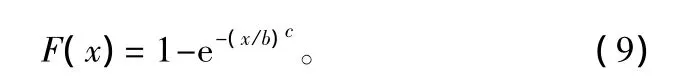
式中:b為尺度參數;c為形狀參數;x為解析木與其周圍相鄰木的最短距離，其取值為0.5，1，1.5，2，…4。

通過SPSS軟件，以長白山地區18塊皆伐標準地的949株云杉解析木與其周圍相鄰木的最近距離對方程(9)進行擬合，得b=1.895，c=2.181，R2=0.996，即:

3.5 修正函數的確定

潛在生長量修正法是直徑生長模型中最常用的方法［8，12］。首先確定林木的潛在生長量，建立疏開木的直徑生長方程，然后用反映立地質量、林分密度、林木最近距離3個競爭指數所表示的修正系數建立修正函數。修正函數的合適與否主要取決于林木競爭指標選擇和組合是否合理，這種方法構造的模型具有結構清晰的優點，而且只要正確選擇疏開木，且所構造的競爭指標能充分有效地反映林木生長的變異，一般都能獲得良好的預測效果。

修正函數MD應滿足以下性質:

①隨FCC的增加，單株樹木的生長空間減小，其生長量隨之減小，即修正函數MD是FCC的減函數，隨FCC值的增加而減小［12］。

②立地條件越好，林地的生產力越高，修正函數MD與立地質量呈正相關。

③修正函數MD取值范圍為:0≤MD≤1。

根據文獻［8］、［12］和修正函數的上述性質可以通過指數函數和冪函數的組合形式確定修正函數。因此組合用數式表示有下列4種情況:

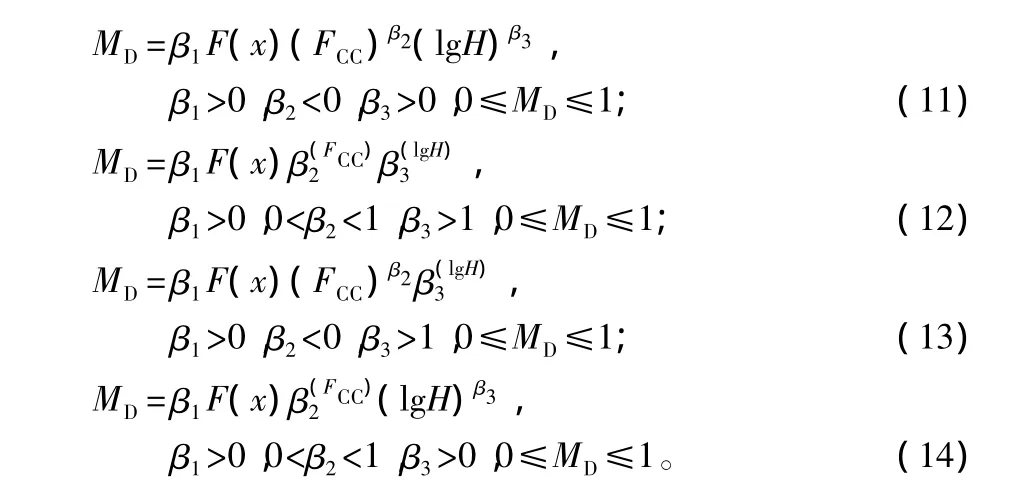
從理論上講，地位級lgH、F(x)的取值范圍在(0，1)，且F(x)為常數。

3.6 胸徑生長的多元回歸模型

將直徑潛在生長方程(方程3)和修正函數MD(方程11至14)代入直徑預測模型D=MD·y中，則得到:

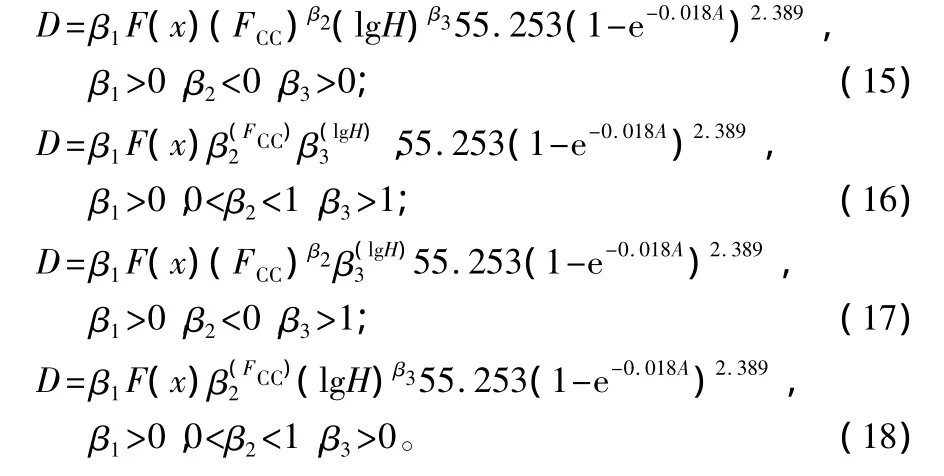
將公式(4)、(8)和(10)分別代入方程(15)至(18)后，采用SPSS軟件，以長白山地區18塊皆伐標準地的949株云杉解析木和78株云杉標準木，進行擬合，依據修正系數0≤MD≤1、相關系數最大和剩余平方和最小，可得方程(17)為直徑實際生長的最佳回歸模型，且參數分別為β1=1.235，β2=－0.090，β3=1.166;相關系數R2=0.931。即直徑生長的多元回歸預測模型為:

3.7 模型的檢驗

為了科學客觀評價擬合效果，采用平均系統誤差(E)、剩余標準差(S)和均方根誤差(Δ)對模型進行檢驗。各公式如下:

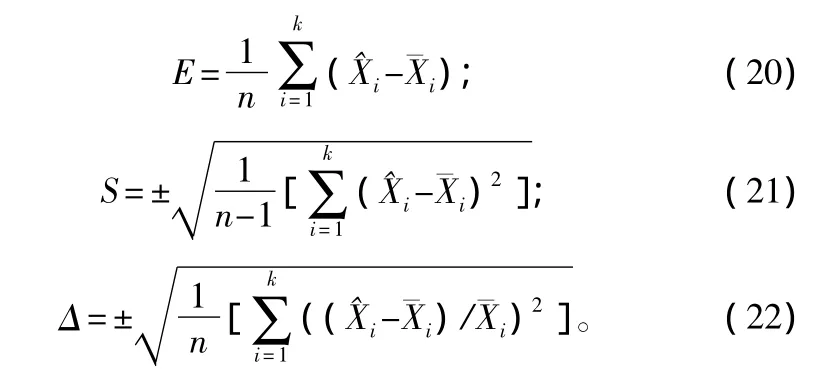
用未參加建模的8塊皆伐標準地的432株云杉解析木和23株云杉標準木，對直徑生長的多元回歸預測模型的擬合度進行檢驗，即以皆伐標準地云杉實測直徑與直徑生長的多元回歸預測模型計算得到的直徑進行比較，得到平均系統誤差的絕對值(|E|)=2.1%＜5%，均方根誤差(Δ)=5.6%＜10%。這說明理論生長量與實際生長量差異不顯著，直徑生長的多元回歸預測模型可用于預估林木直徑的生長，且效果很好，預估的相對誤差為4.52%，估計精度P為95.48%。該模型可以合理預測長白山地區主要樹種林木的未來直徑大小，這對把握林分動態和預估林分生長狀態有極其重要的意義。

4 結論與討論

長白山主要樹種直徑生長的多元回歸預測模型為:D=1.235F(x)(FCC)－0.0901.166lgH55.253(1 －e－0.018A)2.389，對模型進行檢驗，結果顯示其擬合效果很好。該模型可以合理預測長白山地區主要樹種林木的未來直徑大小。

本研究以云杉為例進行分析，對于長白山地區其它主要樹種，如冷杉、紅松和楓樺等，只要有足夠數據，重新擬合求出各方程的參數，就可以對林木直徑的生長進行預估。

在建立直徑生長的多元回歸預測模型時，假設環境條件一致，但從天然異齡林的整個生命過程來看環境因子不應該一直是不變的，因此本模型只適合預測階段性林木直徑結構，沒有考慮采伐強度和采伐周期等因子的影響，在以后的研究中應予以考慮，進一步提高預估精度的準確性。

［1］孟憲宇.測樹學［M］.北京:中國林業出版社，2006.

［2］張青，趙俊卉，亢新剛，等.基于長期歷史數據的直徑結構預測模型［J］.林業科學，2010，46(9):182－185.

［3］孟憲宇.使用Weibull函數對樹高分布和直徑分布的研究［J］.北京林業大學學報，1988，10(1):40－48.

［4］亢新剛，胡文力，董景林，等.過伐林區檢查法經營針闊混交林林分結構動態［J］.北京林業大學學報，2003，25(6):1－5.

［5］胡云云，亢新剛，趙俊卉.長白山地區天然林林木年齡與胸徑的變動關系［J］.東北林業大學學報，2009，37(11):38－42.

［6］Bailey R L.Individual tree growth derived from diameter distribution models［J］.Forest Science，1980，26(4):626－632.

［7］Liu C，Zhang L，Davis C J，et al.A finite mixture model for characterizing the diameter distribution of mixed－species forest stands［J］.Forest Science，2002，48(4):653－661.

［8］孟憲宇，張弘.閩北杉木人工林單木模型［J］.北京林業大學學報，1996，18(2):1－8.

［9］李鳳日，吳俊民，魯勝利.Richards函數與Schnute生長模型的比較［J］.東北林業大學學報，1993，21(4):15－24.

［10］Krajicek J E，Brinkman K A，Gingrich S F.Crown competitiona measure of density［J］.Forest Science，1961，7(1):35－42.

［11］王韓民，惠剛盈.林木最近距離分布模型的研究［J］.林業科學研究，2005，18(5):556－560.

［12］勵龍昌.以潛能函數建立單木生長模型［J］.東北林業大學學報，1990，18(4):22－28.