拉索風(fēng)雨激振的多模態(tài)耦合及面內(nèi)－面外振動

李 暾，陳政清，李壽英

(1.湖南大學(xué) 風(fēng)工程試驗研究中心，長沙 410082;2.廣西工學(xué)院 土木建筑工程系，柳州 545006)

斜拉索在風(fēng)和雨的共同作用下發(fā)生的風(fēng)雨激振［1］，是目前已知的拉索振動類型中振幅最大、危害最嚴重的一種。各國學(xué)者通過現(xiàn)場實測［2－5］、風(fēng)洞試驗［6－7］以及建立各種理論模型［8－11］，對拉索風(fēng)雨激振的發(fā)生機理和振動特性進行了研究。一般認為，拉索表面上水線的形成并在拉索表面的擺動，是造成拉索發(fā)生風(fēng)雨激振的原因。Matsumoto［12］和 Liu［13］則認為由于水線在拉索表面形成的位置不唯一，造成沿拉索軸向卡爾曼渦脫落的頻率和強度不同，從而激發(fā)拉索的高風(fēng)速渦致振動。

通過現(xiàn)場實測和風(fēng)洞試驗，證實了拉索表面運動水線的存在。在現(xiàn)場實測中，還觀測到了拉索的面內(nèi)和面外振動，同時伴隨著拉索模態(tài)的耦合。在風(fēng)洞試驗中，由于試驗條件限制，無法重現(xiàn)該現(xiàn)象。

現(xiàn)有的拉索風(fēng)雨激振理論模型中，節(jié)段拉索模型［8］只能考慮拉索的某階固有頻率，不能反映振動過程中的模態(tài)耦合現(xiàn)象;準運動水線連續(xù)拉索模型［9－10］假設(shè)水線在拉索上整段或在部分區(qū)段形成，并以拉索的某階固有頻率在拉索表面做同步運動，與實際的風(fēng)雨激振現(xiàn)象差別較大，從計算的結(jié)果來看，該類模型反映不了拉索振動的模態(tài)耦合現(xiàn)象;文獻［11］建立的運動水線連續(xù)彈性拉索風(fēng)雨激振模型反映了拉索與水線的耦合運動以及拉索的模態(tài)耦合現(xiàn)象，但該模型只考慮了拉索的面內(nèi)振動，且直接用空間差分法進行求解，不利于對拉索的各階模態(tài)在振動過程中的參與情況做進一步地分析。

本文假設(shè)水線與拉索表面間作用著庫侖阻尼力和粘滯線性阻尼力［14］，同時考慮拉索的面內(nèi)和面外振動，建立了運動水線連續(xù)彈性拉索風(fēng)雨激振理論模型，通過振型分解，得到以拉索各階模態(tài)表示的拉索運動方程，并通過算例做進一步的分析。

1 連續(xù)彈性拉索振動模型

連續(xù)彈性拉索的空間姿態(tài)如圖1所示，其中 α為拉索的傾角;β為風(fēng)向角;x軸為拉索的軸線方向;xoy平面與地面垂直，y軸方向為拉索面內(nèi)振動方向;z軸方向為拉索面外振動方向;U0為來流風(fēng)速。此外，作如下假定:

① 考慮拉索軸向拉伸剛度和彎曲剛度的影響，忽略扭轉(zhuǎn)剛度及剪切剛度的影響;

② 拉索的應(yīng)力－應(yīng)變關(guān)系服從虎克定律;

③ 拉索為張緊的小垂度拉索，其靜止時的線形近似為拋物線;

④ 拉索的質(zhì)量均勻分布;

⑤ 沿拉索軸向的運動忽略不計。

文獻［15］建立了拉索面內(nèi)振動的空間拉索風(fēng)雨激振理論模型，并利用振型分解，得到了以拉索振型坐標表示的拉索運動微分方程。在此，利用相同的方法，可得到以拉索振型坐標表示的同時考慮拉索面內(nèi)振動和面外振動的風(fēng)雨激振運動微分方程:

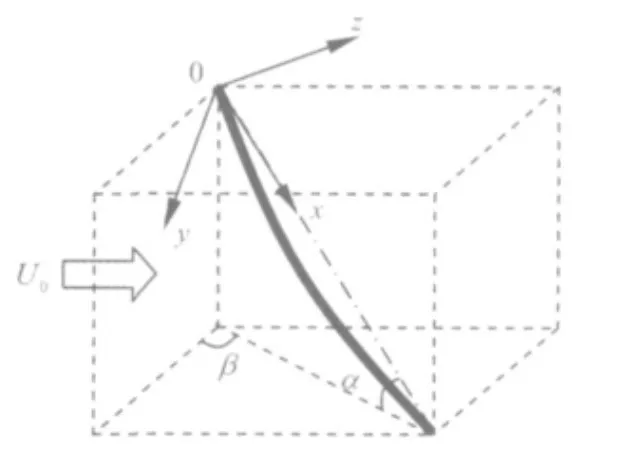
圖1 拉索空間姿態(tài)Fig.1 Position of cable

其中:

式(1)～式(20)中:v，w分別為拉索面內(nèi)和面外振動的動位移;qv，i為拉索面內(nèi)振動第 i階模態(tài)廣義位移;qw，j為拉索面外振動第j階模態(tài)廣義位移;E為彈性模量;I為慣性矩;T0和τ分別為拉索的軸向靜態(tài)和動態(tài)張力;Mc為單位長度拉索的質(zhì)量;Cy、Cz分別為拉索面內(nèi)和面外振動的阻尼系數(shù);Fy、Fz為拉索受到的外荷載(在此為氣動力)在y方向和z方向的分量;t為時間;A為拉索截面面積;λ 為 Irvine 參數(shù);ζv，n、ζw，k分別為拉索面內(nèi)振動第 n 階和面外振動第 k 階模態(tài)阻尼比;ωv，n、ωw，k分別為拉索在考慮非線性情況下面內(nèi)第n階和面外第k階自振頻率;ωv0，n、ωw0，k分別為拉索在不考慮 Irvine 參數(shù)及各模態(tài)之間相互影響時的面內(nèi)第n階和面外第k階自振頻率;ηvs，n、ηws，k分別為拉索抗彎剛度對面內(nèi)第 n階和面外第k階自振頻率的影響系數(shù);ηvλ，n為Irvine參數(shù)對拉索面內(nèi)第 n 階自振頻率的影響系數(shù);ηv，n、ηw，k分別為其余模態(tài)對面內(nèi)第n階和面外第k階自振頻率的影響系數(shù);χv，n為拉索面內(nèi)振動非線性方程中第n階模態(tài)平方項系數(shù);?v，n、?w，k分別為拉索振動非線性方程中面內(nèi)第n階和面外第k階模態(tài)立方項系數(shù);pv，n為其余模態(tài)對拉索面內(nèi)振動第n階模態(tài)的耦合項系數(shù);考慮拉索面內(nèi)振動前N階和面外振動前K階模態(tài)的影響。

2 作用在拉索上的外荷載

取如圖2所示的節(jié)段拉索模型進行研究，并作以下基本假定:

① 水線在運動過程中外形和大小保持不變;

② 準定常假設(shè)成立;

③ 水線與拉索表面間存在粘滯線性阻尼力和庫侖阻尼力［14］;

④ 同時考慮拉索的面內(nèi)振動和面外振動;

⑤ 僅考慮上水線的影響。

圖2 節(jié)段拉索模型Fig.2 Theoretical model of rigid segment of cable

由此，拉索氣動力Fy和Fz的表達式為:

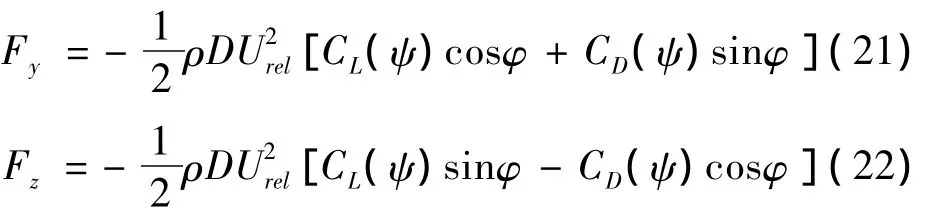
其中:

式中:ρ為空氣密度;D為拉索直徑;CL、CD分別為拉索的氣動升力系數(shù)和氣動阻力系數(shù)，其大小與ψ有關(guān);θ0為水線的初始位置;θ為水線角位移。

3 水線運動偏微分方程

由圖2，可以寫出水線沿拉索表面做周向運動的偏微分方程:

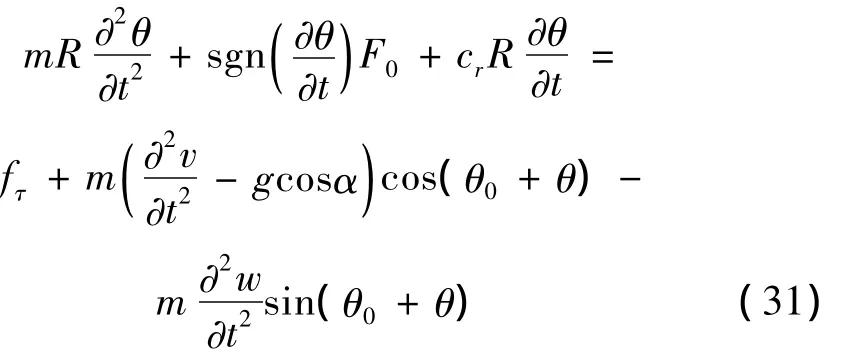
其中:m為單位長度水線的質(zhì)量;R為拉索的半徑;F0為庫侖阻尼力;cr為水線與拉索表面間的粘滯阻尼系數(shù);g為重力加速度;sgn(·)為符號函數(shù);fτ為水線氣動力沿拉索表面切向的分量，其大小為:

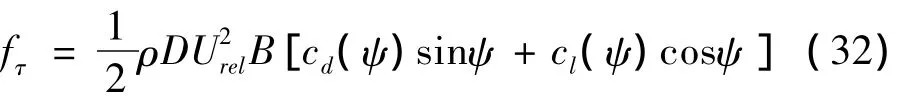
其中:B為水線斷面特征尺寸;cl、cd分別為水線氣動升力和氣動阻力系數(shù)，其大小與ψ有關(guān)。

4 算例

以洞庭湖大橋的S19拉索為例進行分析。S19拉索長182.04 m，單位長度質(zhì)量為56.5kg/m，截面積為0.0072 m2，設(shè)計索力為3504 kN，拉索面內(nèi)和面外的阻尼系數(shù)均為0.5 N·s/m，彈性模量為1.95×105MPa，慣性矩為 4 ×10－6m4，拉索傾角為 30°，風(fēng)向角為35°。由于水線的實際形狀十分復(fù)雜，在理論計算中一般假設(shè)其截面為圓弧形，在此采用文獻［6］中粘貼固定人工水線節(jié)段拉索模型三維測壓時的小水線數(shù)據(jù)，即:單位長度水線質(zhì)量為0.01kg，截面圓弧直徑為13.5mm，弦長9mm，高1.7mm。粘滯阻尼系數(shù)為0.0008 N·s/m2，庫侖阻尼力為 0.0627 N/m［14］。水線在拉索表面的初始位置θ0=1弧度，初始速度為零。風(fēng)速隨高度變化的規(guī)律符合指數(shù)率，既Uh/Ud=(zh/zd)μ，其中zd和Ud分別為橋面距離水面的高度和橋面處的風(fēng)速，zd=25 m;Uh為距離水面高度為h處的風(fēng)速;μ為無量綱冪指數(shù)。洞庭湖大橋處于開闊的水面，取Ⅰ類地貌，μ=0.12;空氣密度為1.225kg/m3。拉索及水線的氣動力系數(shù)取自文獻［6］。

4.1 拉索振動模態(tài)分析

將拉索和水線的數(shù)據(jù)帶入拉索振動方程與水線運動方程，采用龍格－庫塔法進行求解，計算過程中，拉索面內(nèi)和面外振動的模態(tài)分別保留前12階。得到拉索面內(nèi)、面外振動的各階模態(tài)廣義位移后，將其帶入式(3)和式(4)，可以得到拉索各個截面的運動時程。

計算中，Ud從 7.1 m/s開始，每增加0.05 m/s作為一個工況進行求解，每個工況計算過程中風(fēng)速保持不變，得到了在各個風(fēng)速下拉索的振動時程。限于篇幅，圖 3 ～ 圖 5 只給出了 Ud為 8.2 m/s、8.25 m/s和9.35 m/s時拉索面內(nèi)和面外各階模態(tài)的廣義位移時程，以及拉索沿軸線方向上x/L分別為1/6、1/4、1/3和1/2截面處的面內(nèi)和面外振動時程。

從計算的結(jié)果可以看出，在風(fēng)雨激振發(fā)生的過程中，拉索面內(nèi)和面外的多個模態(tài)參與了振動。在開始階段，參振模態(tài)較多;隨著時間的推移，拉索的模態(tài)逐漸轉(zhuǎn)移，最后穩(wěn)定在某幾個(一般有1～3個)模態(tài)上。由于在振動過程中參振模態(tài)的改變，不同風(fēng)速、不同時刻拉索發(fā)生最大振幅的位置并不固定。比如當(dāng)Ud=8.2 m/s時，在前20000 s，拉索的面內(nèi)和面外都有5個參振模態(tài)所占比重相當(dāng)，因此拉索各截面的振幅基本相當(dāng);在20000 s之后，拉索面內(nèi)和面外的參振模態(tài)都逐漸轉(zhuǎn)移到了第2階和第3階，因此拉索在x/L=1/6和1/4截面處的振幅最大，拉索中點處的振幅最小。Ud=8.25 m/s時，前10000 s各階模態(tài)所占成分相當(dāng)，拉索各截面的振幅大致相同;大約16000 s時，面內(nèi)和面外第2階模態(tài)占主要成分，x/L=1/4處的振幅最大;20000 s后，面內(nèi)和面外的第3和第4階模態(tài)占優(yōu)，拉索的最大振幅處轉(zhuǎn)移到了 x/L=1/6處。Ud=9.35 m/s時，開始階段雖然面內(nèi)和面外的第7階模態(tài)參與振動，但在7000 s之后面內(nèi)和面外第7階模態(tài)逐漸退出，參與振動的只剩下面內(nèi)和面外第3階模態(tài)，拉索振幅最大的截面為x/L=1/6和1/2處，x/L=1/3處的振幅幾乎為0。

從圖3～圖5還可以看出，在各個風(fēng)速下，拉索面內(nèi)和面外的第9、10、11、12階這些高階模態(tài)在參振模態(tài)中所占比重很小，幾乎不參與振動;而面內(nèi)和面外的第1階模態(tài)盡管參與了振動，但與主要參振模態(tài)相比，其成分還是少了許多。

從以上的計算結(jié)果還可以發(fā)現(xiàn)，無論在哪個風(fēng)速下，拉索面內(nèi)和面外振動的參振模態(tài)和模態(tài)轉(zhuǎn)移的時刻都是相同的，面內(nèi)和面外振動相對應(yīng)階數(shù)的模態(tài)廣義位移時程的形狀也是基本一樣的，區(qū)別只是其大小不同。由此，拉索各截面的面內(nèi)和面外振動的位移時程形狀基本相同，只是振幅的大小不一樣。圖6是現(xiàn)場實測［3］的拉索風(fēng)雨激振時拉索面內(nèi)和面外振動加速度響應(yīng)時程，映證了本文計算得到的結(jié)論。為敘述方便，在后文中如不特別指明，提到拉索的某階模態(tài)同時指面內(nèi)和面外的模態(tài)。

圖6 洞庭湖大橋拉索加速度響應(yīng)時程Fig.6 Time history of acceleration response of Dongting Lake Bridge cable

此外，圖7給出了拉索面內(nèi)和面外各階模態(tài)在5000 s時和振動穩(wěn)定階段的廣義位移峰－峰值隨風(fēng)速變化的曲線，比較全面的反映了不同風(fēng)速下風(fēng)雨激振過程中拉索各階模態(tài)的變化情況。從圖中可以看出，在振動開始的階段，參與振動的拉索模態(tài)比較多，很難分辨出特別占優(yōu)勢的控制模態(tài);隨著振動的進行，拉索振動的模態(tài)發(fā)生了變化，某幾個(一般是1～3個)模態(tài)逐漸占據(jù)了主導(dǎo)優(yōu)勢，成為主要控制模態(tài)，此時拉索發(fā)生穩(wěn)定的大幅振動。綜合來看，在整個風(fēng)速范圍內(nèi)和振動過程中，主要是拉索的第2～8階模態(tài)參與振動，第1階模態(tài)所占比重不大(即很難激起第1階模態(tài)的振動)，第9及更高階的模態(tài)幾乎不參與振動。

根據(jù)對洞庭湖大橋A10、A12和S19拉索風(fēng)雨激振的現(xiàn)場實測，Ni［3］認為:風(fēng)雨激振時，拉索只發(fā)生單模態(tài)振動的情形是很少的，多數(shù)情況下是幾個模態(tài)共同參與振動。陳政清［2，16］認為:拉索穩(wěn)定的大幅振動總是由某一階模態(tài)控制，通常是第 2、3、4 階。Zuo［4－5］實測到的拉索風(fēng)雨激振參振模態(tài)主要是第2～6階。算例分析得到的結(jié)論與現(xiàn)場實測的結(jié)果是吻合的。

在算例分析中，假設(shè)在0時刻拉索和水線處于靜止狀態(tài)，且水線已經(jīng)在拉索表面θ0=1弧度的位置形成，此時拉索各斷面的氣動力系數(shù)是相同的，因此在振動初始階段，拉索的各階模態(tài)都參與了振動。由于拉索的振動與水線的運動是相互耦合的，因此隨著時間的推移，拉索的振動與水線的運動趨于同步［13］，拉索的參振模態(tài)逐漸轉(zhuǎn)到某幾階主要振型上。文獻［15］對拉索風(fēng)雨激振面內(nèi)振動進行了分析，指出拉索在振動穩(wěn)定階段的主要參振模態(tài)與風(fēng)速的大小和風(fēng)速剖面有很大的關(guān)系。本文建立的理論模型同時考慮了拉索的面內(nèi)和面外振動，對拉索的約束條件比文獻［15］的少，相當(dāng)于增大了拉索的柔度，更接近實際的拉索，因此分析得到的拉索主要參振模態(tài)更接近真實的情況。實際發(fā)生風(fēng)雨激振時，拉索的參振模態(tài)會由于風(fēng)速和風(fēng)向角的改變而發(fā)生轉(zhuǎn)化，雖然在理論分析時不能完全模擬實際的風(fēng)場，但通過對不同風(fēng)速下的拉索振動進行分析，能夠看出風(fēng)速對拉索參振模態(tài)有較大的影響。

4.2 拉索面內(nèi)－面外振動的軌跡

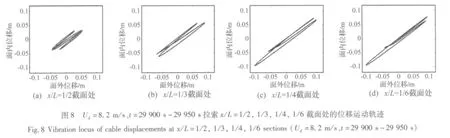
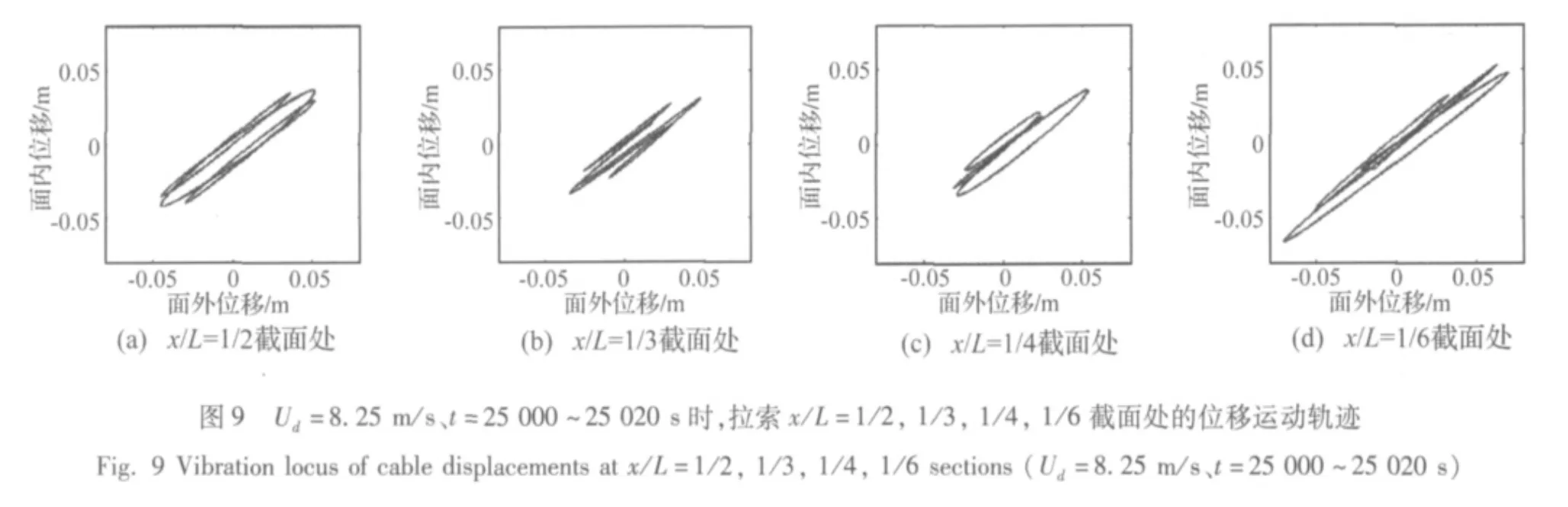
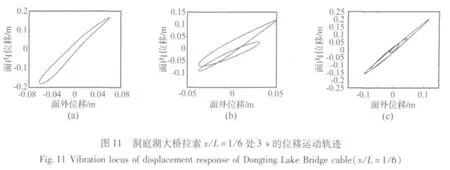
圖8～圖10分別給出了不同風(fēng)速下某一時段內(nèi)拉索某一截面在垂直于x軸的平面內(nèi)的運動軌跡。可以看出，其運動軌跡基本形狀為斜置的橢圓，橢圓的個數(shù)與該時段內(nèi)拉索主要控制模態(tài)的個數(shù)有關(guān)。Ud=8.2 m/s，t=29900 s時，拉索的主要控制模態(tài)是第2和第3階，因此拉索4個截面的運動軌跡為2個斜置的橢圓。Ud=8.25 m/s，t=25000 s時，拉索的振動主要由第 2、3、4階模態(tài)控制，拉索4個截面的運動軌跡為3個斜置橢圓交織在一起。Ud=9.35 m/s，t=9000 s時，拉索振動的主要模態(tài)是第3階，為單模態(tài)振動，因此拉索截面的運動軌跡是1個斜置的橢圓;對于純3階模態(tài)的拉索振動，在x/L=1/3處的位移為0，從圖10可以看出，在該位置處的運動軌跡幾乎為一個點。如果參振的拉索模態(tài)個數(shù)較多，則拉索截面的運動軌跡會比較亂，但其振動的主要方向是基本一致的，限于篇幅，這里沒有給出。

圖11是在洞庭湖大橋?qū)崪y拉索風(fēng)雨激振［3］時記錄的3條拉索在x/L=1/6處3 s時程(由于現(xiàn)場的干擾因素較多，時程太長，則運動軌跡會比較雜亂，不易于分辨其特征)的運動軌跡，其中:圖11(a)是2003年4月1日18:40開始800～803 s的運動軌跡，此時拉索的振動主要由第1階模態(tài)控制;圖11(b)是2003年4月1日20:10開始1200～1203 s的運動軌跡，此時拉索的振動主要由第1、2階模態(tài)控制;圖11(c)是2003年4月1日22:20開始440～443 s的運動軌跡，此時拉索的振動主要由第1、2、3階模態(tài)控制。可以看出，理論計算得到的規(guī)律與現(xiàn)場實測的結(jié)果是比較一致的。

4.3 拉索振動的偏振角

拉索發(fā)生風(fēng)雨激振時，同時伴隨著面內(nèi)振動和面外振動，從拉索的某個截斷面來看，其振動的主軸方向與拉索振動的面內(nèi)方向(y軸方向)或面外方向(z軸方向)有一個夾角，這里定義振動的主軸方向與拉索面外振動方向(z軸方向)的夾角φ為振動的偏振角，如圖12所示。

圖12 拉索振動偏振角Fig.12 Inclination angle of cable vibration

圖13分別給出了在t=5000 s時和振動穩(wěn)定階段拉索x/L=1/6、1/4、1/3和1/2截面處振動的偏振角隨風(fēng)速變化的曲線。從圖中可以看出，同一風(fēng)速下拉索不同截面振動的偏振角基本是一致的，即在同一風(fēng)速下，整根拉索基本上是朝同一方向振動。通過圖13中t=5000 s時和振動穩(wěn)定階段拉索振動偏振角的對比，再結(jié)合圖3～圖5，可以發(fā)現(xiàn)，在某一風(fēng)速下，盡管在不同時刻拉索振動的模態(tài)和振幅是變化的，但拉索振動的偏振角幾乎不隨時間變化。在不同的風(fēng)速下，水線在拉索表面振動時的平衡位置不同，使得拉索在水平方向和豎直方向的氣動力系數(shù)不同，因而影響了拉索振動偏振角的大小。圖13顯示，在7.7～8.7 m/s的風(fēng)速范圍內(nèi)φ＜45°，即拉索的面內(nèi)振動小于面外振動，風(fēng)速范圍占整個拉索振動風(fēng)速范圍的40%;在其余風(fēng)速下φ＞45°，即拉索的面內(nèi)振動大于面外振動，占整個拉索振動風(fēng)速范圍的60%。即使是在7.7～8.7 m/s的風(fēng)速范圍內(nèi)，大部分工況下拉索振動的偏振角一般也在40°～45°之間，即拉索的面內(nèi)振動與面外振動差不多，僅在個別工況下拉索中點處的偏振角在35°左右。因此可以認為:風(fēng)雨激振發(fā)生時，在大部分風(fēng)速范圍內(nèi)，拉索的面內(nèi)振動大于面外振動，而且相對于面外振動，面內(nèi)振動占有較大的優(yōu)勢;在小部分風(fēng)速范圍內(nèi)，拉索的面內(nèi)振動與面外振動差不多，相比面內(nèi)振動，面外振動不占絕對優(yōu)勢。

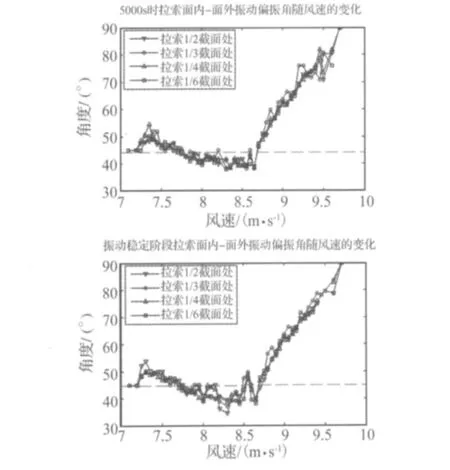
圖13 拉索振動偏振角隨風(fēng)速的變化Fig.13 Variations of cable's inclination angle with different wind velocities

通過對洞庭湖大橋拉索風(fēng)雨激振的實測記錄分析，得到的結(jié)論是:拉索振動時，面內(nèi)、外振動同時發(fā)生，但面內(nèi)振動總是大于面外振動［2］。理論分析的結(jié)論在風(fēng)速較大和較小時與實際情況吻合較好，在中間風(fēng)速段拉索面內(nèi)振動與面外振動基本相當(dāng)，這可能與算例中假設(shè)拉索面內(nèi)和面外振動的阻尼大小是相同的有關(guān)，同時考慮到算例中沒有采用實測時的實際風(fēng)速和風(fēng)向角，可以認為以上得到的規(guī)律與現(xiàn)場實測的結(jié)論是基本吻合的。由于影響拉索振動偏振角的因素十分復(fù)雜，還需要開展大量的工作對其進行分析研究。

4.4 不同風(fēng)速下的拉索振幅

圖14分別給出了t=5000 s時和振動穩(wěn)定階段拉索x/L=1/6、1/4、1/3和1/2截面處位移峰－峰值隨風(fēng)速的變化曲線。同時參考圖7和圖14，可以看出:由于在不同的風(fēng)速下，拉索參振的模態(tài)及各模態(tài)所占的比重不同，使得拉索不同截面振動的峰－峰值隨著風(fēng)速不斷的起伏變化，在整個起振風(fēng)速范圍內(nèi)有幾個極值點，而且各截面振動的峰－峰值隨風(fēng)速變化的趨勢并不相同。

圖14 拉索節(jié)點位移峰－峰值隨風(fēng)速的變化Fig.14 Variations of peak-peak displacements of cable nodes with different wind velocities

對比圖14中t=5000 s和振動穩(wěn)定階段的拉索各截面位移峰－峰值，可以發(fā)現(xiàn)前者隨風(fēng)速的變化比較平緩，而且4條曲線的縱坐標值相差不是很大;而后者隨風(fēng)速的變化比較劇烈，4條曲線的縱坐標值相差比較大。同時對比圖7可以看出，由于在t=5000 s時，不同風(fēng)速下參振的拉索模態(tài)數(shù)較多，而且各參振模態(tài)所占比重相當(dāng)，使得拉索各截面的位移峰－峰值相差不大，且隨風(fēng)速的變化相對平緩;隨著振動的發(fā)展而伴隨的拉索參振模態(tài)的轉(zhuǎn)移，到達振動穩(wěn)定階段，拉索的參振模態(tài)穩(wěn)定在少數(shù)幾個主要控制模態(tài)上(一般情況下是2～3個，個別風(fēng)速下是單模態(tài)振動)，而且不同的風(fēng)速下的主要控制模態(tài)并不相同，使得拉索不同位置處的位移峰－峰值相差比較明顯，且隨風(fēng)速的變化比較劇烈。拉索最大振幅發(fā)生在Ud=8.3 m/s風(fēng)速下，x/L=1/6處的位移峰－峰值達到了0.27 m，約為拉索直徑的3倍。

通過對每隔0.05 m/s的風(fēng)速逐一計算，得到S19拉索的起振風(fēng)速范圍是7.2～9.7 m/s，而在對洞庭湖大橋拉索風(fēng)雨激振的實測時記錄的風(fēng)速范圍是6～20 m/s［2］，計算的風(fēng)速范圍在實測記錄的風(fēng)速范圍內(nèi)。圖14同時反映了“限速”、“限幅”的風(fēng)雨激振特征。

5 結(jié)論

在假設(shè)拉索表面與水線之間作用著庫侖阻尼力和粘滯線性阻尼力的基礎(chǔ)上，建立了能夠反映拉索面內(nèi)－面外振動的帶運動水線的連續(xù)彈性拉索風(fēng)雨激振理論模型。利用該模型對洞庭湖大橋S19拉索進行計算，得到了在不同風(fēng)速下拉索各階模態(tài)的廣義位移響應(yīng)，在此基礎(chǔ)上得到了拉索上某個指定截面的位移響應(yīng)、運動軌跡和振動偏振角。通過對計算結(jié)果的分析，得到以下規(guī)律:

(1)拉索發(fā)生風(fēng)雨激振時，通常有多個模態(tài)共同參與，表現(xiàn)為多模態(tài)的耦合振動;

(2)在振動過程中會發(fā)生模態(tài)的轉(zhuǎn)移，當(dāng)振動穩(wěn)定在2～3個主要控制模態(tài)(少數(shù)情況下是單模態(tài)振動)時，拉索發(fā)生穩(wěn)定的大幅振動;

(3)風(fēng)雨激振發(fā)生時，拉索同時發(fā)生面內(nèi)和面外振動，在同一風(fēng)速下，對應(yīng)的面內(nèi)和面外振動模態(tài)廣義位移響應(yīng)以及相應(yīng)的拉索面內(nèi)和面外振動的位移響應(yīng)時程曲線形狀基本是一樣的，區(qū)別只在于其值大小不同;

(4)拉索截面的運動軌跡基本形狀為斜置的橢圓，一般情況下是幾個斜置橢圓交織在一起，斜置橢圓的個數(shù)與拉索參振模態(tài)的個數(shù)相同;

(5)在同一風(fēng)速下，整根拉索基本上是朝同一偏振角方向振動，而且在整個振動時段內(nèi)，拉索振動的偏振角幾乎沒有變化;

(6)起振風(fēng)速對拉索振動偏振角的影響較大，在大部分起振風(fēng)速范圍內(nèi)，面內(nèi)振動大于面外振動，在其余風(fēng)速范圍內(nèi)，面內(nèi)振動與面外振動的振幅相差不大;

(7)拉索發(fā)生最大振幅的位置隨參振的主要控制模態(tài)不同而變化，拉索不同截面的位移峰－峰值隨風(fēng)速變化的曲線呈現(xiàn)幾個極值點，且變化趨勢不相同。

通過與現(xiàn)場實測的觀測記錄進行對比，本文計算分析得到的規(guī)律與現(xiàn)場實測總結(jié)的拉索風(fēng)雨激振特征基本吻合。本文建立的理論模型夠比較真實的反映實際的拉索風(fēng)雨激振現(xiàn)象，建立理論模型時所作的假設(shè)是基本合理的。

［1］Hikami Y，Shiraishi N.Rain-wind induced vibrations of cables in cable stayed bridges［J］. JournalofWind Engineering and Industrial Aerodynamics，1988，29(2):409－418.

［2］陳政清.斜拉索風(fēng)雨激振現(xiàn)場觀測與振動控制［J］.建筑科學(xué)與工程學(xué)報，2005，22(4):5－10.

［3］Ni Y Q，Wang X Y，Chen Z Q，et al.Field observations of rain-wind-induced cable vibration in cable-stayed Dongting Lake Bridge［J］.Journal of Wind Engineering and Industrial Aerodynamics，2007，95(5):303 －328.

［4］Zuo D，Jones N P，Main J A.Field observation of vortex-and rain-wind-induced stay-cable vibrations in a three-dimensional environment［J］.Journal of Wind Engineering and Industrial Aerodynamics，2008，96(6－7):1124－1133.

［5］Zuo D L，Jones N.Interpretation of field observations of wind-and rain-wind-induced stay cable vibrations［J］.Journal of Wind Engineering and Industrial Aerodynamics，2010，98(2):73－87.

［6］Gu M，Du X Q，Li S Y.Experimental and theoretical simulations on wind rain-induced vibration of 3－D rigid stay cables［J］.Journal of Sound and Vibration，2009，320(1 －2):184－200.

［7］Zhan S，Xu Y L，Zhou H J，et al.Experimental study of wind-rain-induced cable vibration using a new model setup scheme［J］.Journal of Wind Engineering and Industrial Aerodynamics，2008，96(12):2438－2451.

［8］李壽英，陳政清，顧 明.斜拉橋拉索風(fēng)雨激振的兩質(zhì)量三自由度理論模型［J］.土木工程學(xué)報，2007，40(10):60－66.

［9］李壽英，顧 明，陳政清.準運動水線三維連續(xù)彈性拉索風(fēng)雨激振理論模型［J］.工程力學(xué)，2007，24(6):7－14.

［10］Xu Y L，Wang L Y.Analytical study of wind-rain-induced cable vibration:SODF model［J］. JournalofWind Engineering and Industrial Aerodynamics，2003，91(1):27－40.

［11］李壽英，顧 明，陳政清.運動水線三維連續(xù)彈性拉索風(fēng)雨激振理論模型［J］.湖南大學(xué)學(xué)報(自然科學(xué)版)，2009，36(2):1－7.

［12］Matsumoto M，Yagi T，Goto M，et al.Rain-wind-induced vibration of inclined cables at limited high reduced wind velocity region［J］.Journal of Wind Engineering and Industrial Aerodynamics，2003，91(1):1 －12.

［13］Liu Q K.The effects of water rivulet and axial flow on cable aerodynamics of cable-stayed bridges［D］.Kyoto:Kyoto University，2006.

［14］李 暾，陳政清，李壽英.拉索表面材料對風(fēng)雨激振的影響研究［J］.工程力學(xué)，2009，26(7):47－53.

［15］李 暾，陳政清，李壽英.連續(xù)彈性拉索風(fēng)雨激振理論模型研究［J］.振動工程學(xué)報，2010，23(4):380－388.

［16］陳政清.橋梁風(fēng)工程［M］.北京:人民交通出版社，2005，5.