旅行商問題圖論近似算法有效性分析

林農

(東莞理工學院 計算機學院，廣東東莞 523808)

旅行商問題圖論近似算法有效性分析

林農

(東莞理工學院 計算機學院，廣東東莞 523808)

給出旅行商問題四種圖論近似算法及有效性分析，改進第一種近似算法證明，修正第二、三、四種近似算法有效性的上界。

旅行商問題;NP難題;圖論;近似算法;算法有效性

旅行商問題是組合數學中著名的NP難題［1，2］，它在實際中有著廣泛而深入的應用，在超大規模集成電路設計和路徑規劃都有重要應用價值，它的計算復雜性研究在形成NP完全理論中起到奠基作用［3］。因而這幾年對它的研究一直是熱點問題。目前對它的研究方法有兩類，第一類：思想性和構造性方法，如分支限界法和近似算法。第二類：隨著智能算法在各個領域的應用，而產生的一些仿生優化算法，如遺傳算法和螞蟻算法，這一類方法和經典組合數學方法結合，能夠加速算法速度，提高解的質量［3］。本文在旅行商問題的四種圖論近似算法的基礎上，對第一種近似算法證明給予改進，對第二、三、四種近似算法效率的上界給予修正。

1 最近鄰法［4］

算法思想和基本步驟：

1) 從一個頂點開始，令P=(j1)。

2) 設當前路徑為P=(j1，j2，…，jk)，從尚未搜查的n-k個頂點中加入和jk，最鄰近的點jk+1，得到新的路徑 P=(j1，j2，…，jk，jk+1)，直至包含 n 個頂點。

3)連接起始頂點和終止頂點，得到就是最近鄰法的旅行回路。設最短哈密頓回路長度為，最近鄰法旅行回路長度為Nn。

證明 設結點集 A={v1，v2，…，vmin{2k，n}}，

使得與vi相關聯的最短邊li，滿足l1≥l2≥…≥lmin{2k，n}。

由最近鄰法知：dij≥min{li，lj}，

故

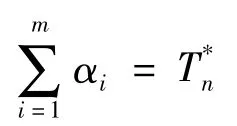
其中至多有k個αi=0，則至少有min{2k，n}－k個αi=2，

在最小的情況下，k個 αi=0，對應l1，l2，…，lk，

min{2k，n}－ k 個 αi=2 ，對應 lk+1，lk+2，…，lmin{2k，n}，

(證畢)

2 最近鄰插入法［4］

算法思想和基本步驟：

1)從一個頂點開始，構造不斷擴大的回路。

2)設包含k個頂點的最佳回路為Tk，加入和Tk最鄰近的頂點，插入位置使得回路增量最小，成新的最佳回路Tk+1，直至包含n個頂點，即得最近鄰插入法旅行回路。設最短哈密頓回路長度為，最鄰近插入法旅行回路長度為In。

由最近鄰插入法知，存在旅行回路上點p，及點p相鄰但不在旅行回路上點q(有時q=i)，及點i在同一道路上。這樣點i和邊pq建立一一對應關系。當插入點i時，回路增量記為δi，則δi=dij+dikdjk。

δi和dpq的關系如下：

由三角不等式，有dik-djk≤dij，從而 δi=dij+dik-djk≤2dij，又由最近鄰插入法，有dij≤dpq，因此δi≤2dpq。

In和T*n的關系如下：

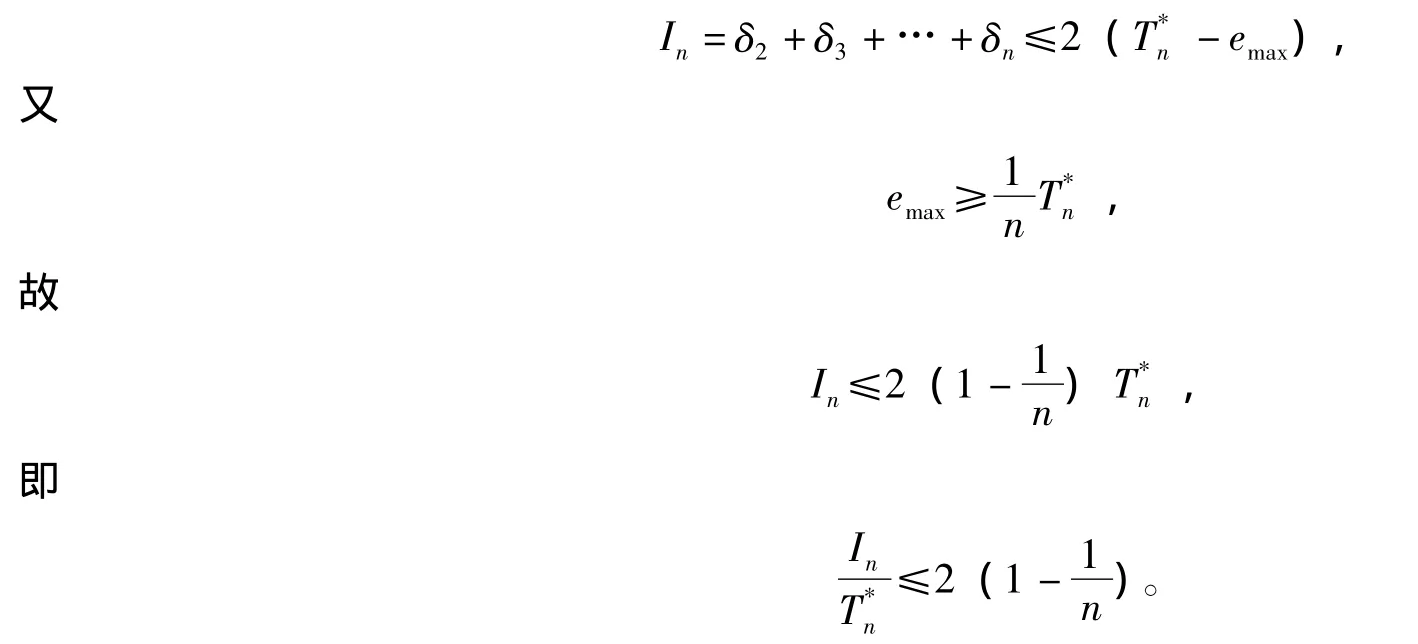
(證畢)

3 生成樹加倍算法［5］

算法的思想和基本步驟：

1)求最小生成樹;

2)利用深探法遍歷最小生成樹，回頭時遍歷邊計算在內，即每條邊計算兩次，得一回路;

3)刪除回路中后面重復出現的結點，最后一個除外，得生成樹加倍算法旅行回路。

證明

(證畢)

4 生成樹加匹配算法［5］

算法的思想和基本步驟：

1)求最小生成樹;

2)最小生成樹上的奇點，共有偶數個，求最小權匹配;

3)最小生成樹及最小生成樹奇點的最小權匹配構成歐拉圖，求歐拉回路;

4)刪除歐拉回路中后面重復出現的結點，最后一個除外。即得生成樹加匹配算法旅行回路。

定理4 算法有效性為

設訪問最小生成樹上奇次結點的順序和訪問最短哈密頓回路結點的順序相同，得到一個回路。該回路有偶數個結點，可以分解成兩個匹配M1，M2。

由三角不等式，得

(證畢)

［1］Lawler E L，Lenstra J K，Rinnooy Kan A H G，et al．The traveling salesman problem：a guided tour of combinatorial optimization［M］．New York：Wiley，1985．

［2］Garey M R，Johnson D S．Computers and intractability：a guide to the theory of NP-Completeness［M］．San Francisco：W H Freeman，1979．

［3］陳繼業．旅行商問題的近似算法研究［D］．長沙：國防科技大學，2005．

［4］盧開澄．計算機算法導引-設計與分析［M］．2版．北京：清華大學出版社，2006：276-384．

［5］謝政，李建平．網絡算法與復雜性理論［M］．長沙：國防科技大學出版社，1995：332-353．

An Analysis of the Effectiveness of Approximate Algorithms Based on Graph Theory for the Traveling Salesman Problem

LIN Nong
(College of Computer，Dongguan University of Technology，Dongguan 523808，China)

Based on graph theory and their effectiveness，four approximate algorithms are given，adapting the proof technique of the first，modifying the upper bound of the second，third and fourth ．

traveling salesman;graph theory;approximate algorithm;effectiveness of algorithm

O157．5;TP301．6

A

1009-0312(2012)01-0010-04

2011-04-12

林農 (1975—)，女，福建龍巖人，講師，碩士，主要從事圖論及其算法研究。