貝葉斯網絡用于屏蔽泵系統故障分析方法的研究

鮑依蘭，黃高峰，佟立麗，曹學武

（上海交通大學機械與動力工程學院，上海200240）

貝葉斯網絡（Bayesian Network，BN）是基于概率論和圖論的一種不確定性知識表達和推理網絡，最早由Judea Pearl［1］于1988年提出，研究其在機器學習、數據挖掘及數據統計的應用，近年來，貝葉斯網絡在人工智能領域得到不斷發展和改進，使其成為不確定推理中最有力的工具，貝葉斯網絡已成功應用于計算機智能科學、醫療診斷和工業控制等眾多領域。目前，系統故障分析常用的方法是故障樹模型分析方法，故障樹分析法適用于故障機理、故障邏輯關系清晰的系統，需要對系統的故障樹模型做簡化假設：事件狀態的二態性、基本底事件間相互獨立和故障邏輯關系的確定性［2］。而事實上閥門存在正常、拒開和破裂等多故障狀態，許多故障間的因果關系是不確定性的邏輯關系，以及在獲得新的故障樣本后希望對分析數據能夠及時更新，對系統的故障進行及時準確分析等問題，因此，本文以屏蔽泵系統故障分析為實例，應用貝葉斯網絡解決實際系統故障分析中的問題，最后由貝葉斯網絡自身強大概率推理能力［3－4］對屏蔽泵系統故障狀態進行及時有 效分析。

1 貝葉斯網絡模型

貝葉斯網絡［1］是一個有向無環圖（Directed Acyclic Graph，DAG），由代表變量的節點及連接這些節點的有向弧構成，有向弧由父節點指向子節點，用單線箭頭“→”表示。BN由網絡拓撲結構和局部條件概率表（Conditional Probability Table，CPT）兩部分構成，沒有任何父節點的節點稱為根節點，對應的條件概率稱為先驗概率。通過定義網絡中所有節點、節點間的關聯（用有向弧表示）和指定條件概率表，就能表達BN中所有節點的聯合概率，并且可以在已知任意節點狀態信息條件下，進行網絡推理，計算其他任意節點的條件概率。

1．1 貝葉斯網絡學習

為了獲得貝葉斯網絡，把通過機器學習的方法從數據中獲得BN的方法稱為BN學習［5，6］，BN 學習可分解為兩個階段：一是，網絡拓撲結構即有向無環圖的學習，簡稱結構學習；二是，網絡中每個變量的局部條件概率分布的學習，簡稱參數學習。本文貝葉斯網絡結構是由故障樹模型轉化方法獲得，該方法具有簡單可行的優點［2～4］，本文主要研究BN參數學習，視參數θ為一個隨機變量，采用貝葉斯估計方法，利用先驗知識和數據樣本對參數進行估計，獲得其后驗概率分布，貝葉斯估計公式如式（1）所示：

式中：L（D｜θ）表示數據樣本D的影響，稱為似然函數，它是網絡節點的狀態變量樣本觀測值，可根據經驗統計和記錄確定節點狀態的似然函數，對應π（θ）用于表示先驗知識，稱為先驗概率分布函數，它是網絡節點事件的發生概率，可根據歷史資料或主觀判斷確定節點事件的先驗概率分布。在貝葉斯方法中，合理的先驗概率分布π（θ）確定是容易引起爭議［5，7］，另外核電廠設備故障分析數據匱乏和僅從一個特定電廠的運行經驗結果不具有統計意義，本文采用共軛先驗分布和設備故障的國際通用數據確定先驗知識，主要針對設備故障分析數據中的兩個重要參數：需求失效概率和運行失效率，通過貝葉斯網絡學習來確定它們的后驗分布參數估計。

1．2 共軛先驗分布族

實際應用中根據公式（1）計算后驗分布密度是比較復雜的，因此，Raiffa和Schaifeer提出共軛分布族。根據文獻［7］的研究，需求失效概率（pi）和運行失效率（λ）的共軛先驗分布可分別采用樣本來自平穩獨立二項式分布過程的Beta分布和樣本來自平穩獨立Poisson分布過程的 Gamma分布［7］，因此，pi和λ的Bayes估計可分別由下面公式（3）和（5）來確定。

進行m次設備需求失效試驗或運行失效試驗，在第i（i＝1，2，…，m）次試驗中，試驗時間為ti（t1＜t2＜…＜tm），對應的試驗設備樣本數為ni，若試驗結果有ri（ri＝0，1，…，ni）個失效（對應設備需求失效次數或設備運行失效次數），記（ti，ni，ri），i＝1，2，…，m 為本次試驗獲得的數據。

1．2．1 設備需求失效概率的Bayes估計

在需求失效試驗中，假設失效次數ri是一個二項分布過程，根據pi的共軛先驗分布和公式（1），設備需求失效概率pi的后驗分布函數如公式（2）所示：

用pi后驗函數的數學期望，作為設備需求失效概率pi的Bayes估計，后驗需求失效概率pi是先驗參數和樣本失效次數的函數，如公式（3）所示：

1．2．2 設備運行失效率的Bayes估計

在設備運行失效試驗中，假設失效次數ri是泊松分布，根據λ的共軛先驗分布和公式（1），設備運行失效率λ的后驗分布函數如公式（4）所示：

若運行失效概率服從指數分布，則在給定任務時間t內的運行失效概率由公式（6）計算：

1．3 貝葉斯網絡推理

貝葉斯網絡是建立在節點變量的概率約束上，表達了節點變量間的條件獨立性，基于網絡結構（定性）和參數（定量）知識可以進行不確定性雙向推理計算［8］。貝葉斯網絡正向推理獲得網絡中節點的聯合概率和任意節點發生概率，其數學描述為：論域中U＝｛x1，x2，…，xn｝對應于網絡中的節點，pparents（xi）表示xi父節點的集合，聯合概率p（x1，x2，…，xn）如公式（7）所示：

貝葉斯網絡反向推理獲得在已知某些節點信息條件時的其他節點的條件概率，例如，隨機變量xi具有 m 個事件狀態｛xi1｝，｛xi2｝，…，｛xim｝，假設已知其他節點的信息為V，則在該已知條件下xi處于各事件狀態的發生概率由公式（8）計算：

2 基于貝葉斯網絡的屏蔽泵故障分析

故障樹分析方法（Fault Tree Analysis，FTA）是一種將系統故障形成的原因由總體至部分按樹枝狀細化的分析方法，是系統概率安全分析和故障分析的一種重要方法。本文基于故障樹模型中各相關事件間的因果關系構建屏蔽泵故障的貝葉斯網絡拓撲結構，故障樹模型轉換獲得貝葉斯網絡得到研究［2，3］。

2．1 屏蔽泵故障的貝葉斯網絡拓撲結構

本文建立的屏蔽泵故障貝葉斯網絡結構如圖1所示，論域中共有43節點事件，第43節點為屏蔽泵故障事件T，網絡中其他節點事件定義和編碼見表1。

2．2 基于BNT的屏蔽泵故障貝葉斯網絡參數學習

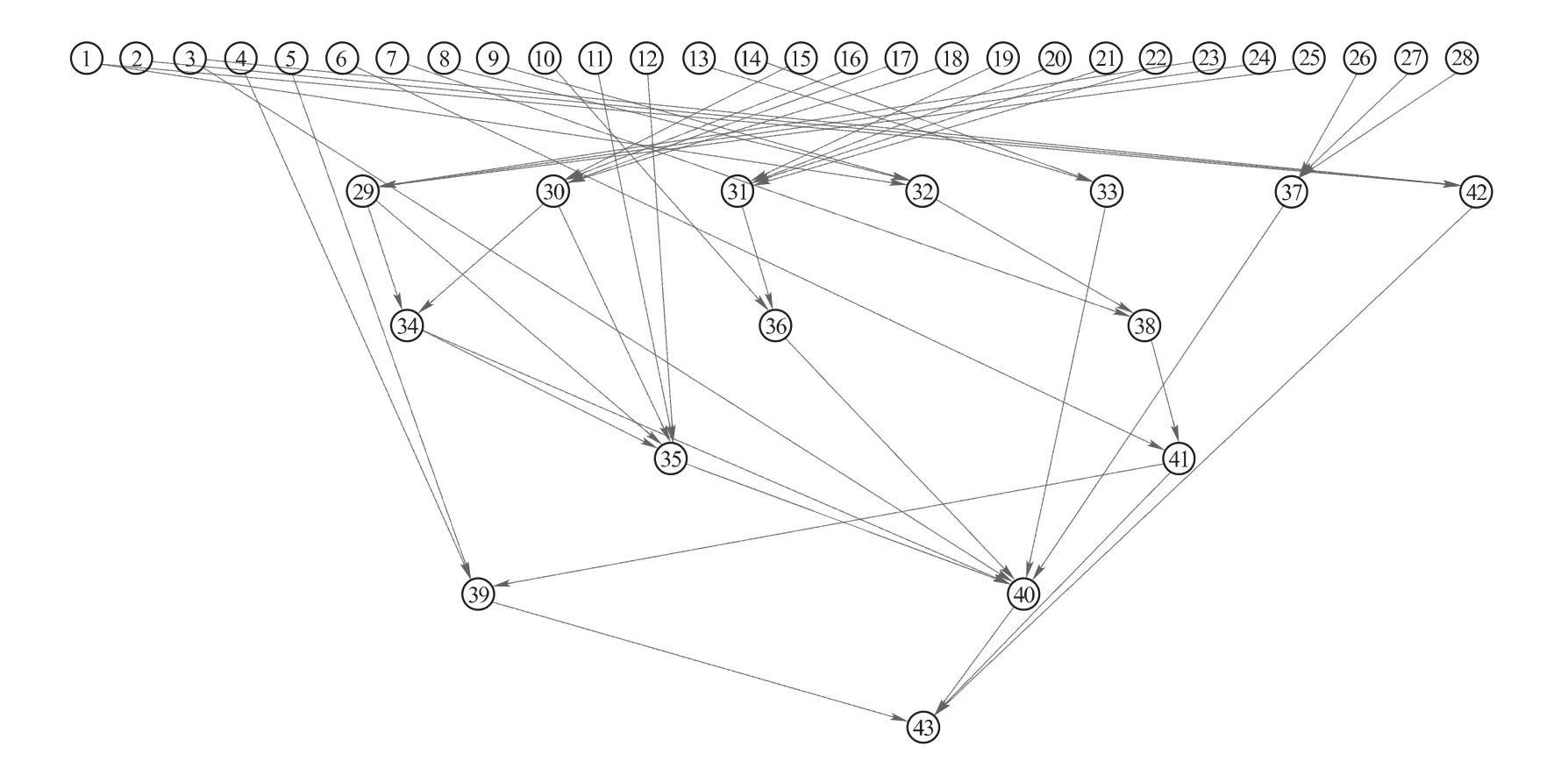
圖1 屏蔽泵故障的貝葉斯網絡Fig．1 Fielded pump failure Bayesian network

表1 模型中各節點事件定義Table 1 Definition of each nodes event in model

采用MATLAB語言編制的貝葉斯網絡工具箱（Bayesian Networks Toolbox，BNT），進行屏蔽泵故障貝葉斯網絡參數學習和推理，此工具箱在貝葉斯學習編程方面非常靈活。但BNT中僅提供了Beta先驗分布的參數學習機制，可以獲得設備需求失效概率的估計，而為了計算運行失效率參數，本文基于上一節貝葉斯網絡學習理論，在BNT軟件中新增先驗分布為Gamma分布的失效率參數學習機制。屏蔽泵故障貝葉斯網絡中初始先驗參數假定，令根節點X2和X3為設備失效率事件，失效率先驗參數基于Jeffreys的無信息Gamma先驗分布；其他節點事件是設備需求失效事件，失效概率先驗參數基于Jeffreys無信息Beta（0．5，0．5）先驗分布［7］。另外節點狀態變量說明，貝葉斯網絡具有多狀態表達能力，本文例舉研究，當根節點X22為三狀態時候，對應事件描述為：腐蝕嚴重、無腐蝕和一般腐蝕，節點狀態值分別為“1、2和3”，其他網絡節點為二態，狀態取值為：“1”表示節點事件故障狀態，“2”表示節點事件正常狀態。為了描述方便，將該初始網絡稱為bnet1網絡。

在屏蔽泵系統設備故障統計中，能夠收集到相關設備失效概率的通用數據，在網絡bnet1先驗參數基礎上，本文用BNT軟件中參數學習機制，獲得各根節點的通用數據，進一步討論獲得新樣本后的進行網絡參數學習，表明了貝葉斯網絡不僅具有學習功能，還能在新信息條件下不斷更新，獲得設備新樣本下故障分析。因此，本文進行了二次網絡參數學習，第一次參數學習獲得根節點通用數據的網絡稱為bnet2，第二次在新樣本數據下的參數更新學習，獲得的網絡稱為bnet3。

圖2是三個網絡（bnet1、bnet2和bnet3）所有節點的部分參數比較，發現：一、bnet2網絡中各根節點的參數為相應通用數據；二、bnet3在獲得新樣本后，得到進一步網絡參數更新，由圖22中bnet2和bnet3曲線可見，節點X3和A1的參數變化較大。分析變化原因：節點X3參數是由公式（6）計算得到，失效率參數在學習中與新樣本中運行失效次數有關和試驗運行時間有關，兩者使得節點X3參數的變化；另外，節點A1參數是失效概率參數學習，它僅與新樣本中出現的需求失效次數有關，當新樣本中出現節點A1失效事件，由公式（3）計算出新樣本下的參數。三、對比bnet1先驗參數，bnet2和bnet3網絡參數學習后，可獲得中間節點的邏輯關系。如故障樹模型中B1和B3節點與上層節點的分別是“邏輯與”和“邏輯或”關系，圖3和圖4分別是它們在三個網絡中的CPT，由圖可見，經過學習的網絡參數可表達，“邏輯與”：當父節點事件全部發生時，B1節點發生事件對應的CPT值大于0．9，否則B1節點發生事件對應的CPT值小于0．1；“邏輯或”：只要有一父節點發生，B3節點發生事件對應的CPT值大于0．9，否則B3節點發生事件對應的CPT值小于0．1。四、BN可以表達多狀態事件，圖5是網絡中三狀態節點X22對應的參數值，可以看出先驗分布的bnet1網絡參數經過樣本學習后，獲得節點事件各狀態時的發生概率，貝葉斯網絡表達多狀態事件比故障樹模型簡單方便。

圖2 bnet1、bnet2和bnet3貝葉斯網絡參數學習比較Fig．2 Network parameters comparison of bnet1，bnet2 and bnet3 network

圖3 三個貝葉斯網絡中“邏輯與”節點B1的參數CPTFig．3 Parameters comparison of“logic and”B3 node in three Bayesian networks

圖4 三個貝葉斯網絡中“邏輯或”節點B3的參數CPTFig．4 Parameters comparison of“OR logic”T node in three Bayesian networks

圖5 三個貝葉斯網絡中多態節點X22的參數CPT值Fig．5 Parameters CPT comparison of multi-fault state node in three Bayesian networks

2．3 屏蔽泵故障貝葉斯網絡的推理

貝葉斯網絡具有雙向推理功能，定量地給出各元件在系統可靠性中所占的地位，本文通過貝葉斯網絡推理分析屏蔽泵系統故障的薄弱環節所在、出現最可能的故障模式及其發生概率。

2．3．1 未知證據的貝葉斯網絡推理

首先計算在沒有證據時各節點全概率，它體現了在證據未知情況下，對各種節點事件的一種置信度（表2），是屏蔽泵故障節點T及其父節點的發生概率。

表2 未知證據時屏蔽泵故障及其父節點事件的概率值Table 2 The failure probability of fielded pump and parent node event in no-evidence case

表2中橫項是三個學習網絡的推理結果，列項是屏蔽泵故障與各節點的發生概率，可看出無證據時屏蔽泵故障的概率為0．9411，而且對其貢獻最大的是振動異常，其次是出口流量不足，而定子燒結對其影響很小。另外，發現網絡bnet3的屏蔽泵故障概率比bnet2高，因此，獲得新樣本后對網絡參數進行更新是很有必要。

2．3．2 已知簡單證據的貝葉斯網絡推理

若現在調研獲知葉輪破損，對應根節點X2發生狀態為“1”時，此時可以由網絡正向推理進一步獲得，在該證據時屏蔽泵系統故障和其他節點的故障信息，如表3所示。

表3 已知evidence｛X2｝＝1證據時屏蔽泵故障及其父節點事件的概率值Table 3 The failure probability of fielded pump and parent node event in evidence｛X2｝＝1 case

從表3發現，經過參數學習后的網絡bnet2和bnet3，在已知葉輪破損后，“出口流量不足”事件的發生概率大大提高，并預測到此時屏蔽泵故障發生概率比無證據時大。總結，通過貝葉斯網絡可以得到在給定任意節點證據時，各層節點事件的發生概率，找出對屏蔽泵故障影響最大的事件，在實際工作中首先對這些事件進行維修。

2．3．3 屏蔽泵系統故障分析

上述主要比較了通過參數學習獲得的三個網絡，為了剖析屏蔽泵系統故障，下面對網絡bnet2在已知屏蔽泵故障證據（節點T發生）時進行后向推理，分析屏蔽泵系統的故障原因，找到系統的薄弱環節。

（1）如下各根節點對屏蔽泵故障影響排序（號碼為各節點的編號），可得屏蔽泵故障主要受節點X3的影響，對應事件是“泵入口壓力過低”事件，其次是節點X11和節點X1，對應“電壓波動”和“輸入電壓過低”事件的影響也較大。

（2）已知evidence｛T｝＝1證據，計算聯合節點［X1，X2］和［X22，C2］的概率分布，分別如圖6和圖7所示。由圖6得出，屏蔽泵故障由于節點X1和X2同時故障導致可能性很小；由圖6得出，節點X22增加“事件狀態3”，該狀態對屏蔽泵故障的概率貢獻見圖7第三個分布，可見是不容忽略的狀態。

圖6 bnet2網絡在evidence｛T｝＝［1］證據時［X1 X2］的聯合概率分布Fig．6 The joint probability［X1 X2］of bnet2 in evidence｛T｝＝［1］case

圖7 bnet2網絡在evidence｛T｝＝［1］證據時［X22 C2］的聯合概率分布Fig．7 The joint probability［X22 C2］of bnet2 in evidence｛T｝＝［1］case

（3）表4是bnet2網絡在屏蔽泵系統故障時的推理分析，屏蔽泵系統中最大可能的故障模式是：泵入口壓力過低、振動異常和出口流量不足導致屏蔽泵故障。

表4 網絡bnet2對屏蔽泵系統故障的推理分析Table 4 The inference analysis to fielded pump failure in bnet2 network

3 結論

與故障樹分析方法比較，貝葉斯網絡具有表達多故障狀態和不確定性邏輯關系的能力，本文建立含有多狀態節點的屏蔽泵故障貝葉斯網絡模型，并在貝葉斯網絡工具箱軟件中，新增設備故障運行失效率參數的學習機制，通過對網絡中參數的學習，獲得根節點發生概率為通用數據的網絡和進行新樣本學習后的網絡，最后由網絡推理剖析屏蔽泵系統故障原因，屏蔽系統故障分析的結論為：泵入口壓力過低、電壓波動和輸入電壓過低是屏蔽泵系統的薄弱環節，振動異常和出口流量不足是屏蔽泵故障的直接原因。綜上，貝葉斯網絡能夠用簡潔直觀的圖形描述系統中各單元部件間復雜的因果關系和多狀態故障事件，并在網絡節點有新樣本信息時，貝葉斯網絡的學習機制可更新網絡參數，結合先驗知識和樣本信息，由貝葉斯網絡強大的不確定性推理能力，給出詳細的概率解釋，因此，貝葉斯網絡能夠作為故障分析方法，為研究系統故障模式和機理提供有效途徑。

［1］ Pearl J．Probabilistic Reasoning in Intelligent Systems：Networks of Plausible Inference ［M］．Revised second Printing，Morgan Kaufmann Publishers，Inc 1988．

［2］ 王廣彥，馬志軍，胡起偉．基于貝葉斯網絡的故障樹分析［J］．系統工程理論與實踐，2004，24（6）：78-83．

［3］ 周忠寶，董豆豆，周經倫．貝葉斯網絡在可靠性分析中應用 ［J］．系統工程理論與實踐，2006，（6）：95-100．

［4］ Bobbio A，Portinale L，Minichino M，et al．Improving the analysis of dependable systems by mapping fault trees into Bayesian networks［J］．Reliability Engineering System Safety，2001，71（3）：249-260．

［5］ 林士敏，王雙成，盧玉昌．貝葉斯方法的學習機制與問題求解 ［N］．清華大學學報，2000，40（9）：61-64．

［6］ Cooper Gregory F，Edward Herskovits．A Bayesian Method for the Induction of Probabilistic Networks from Data［J］．Machine Learning，1992，l9（4）：309-347．

［7］ 馬靜嫻，嚴國奎，劉志軍．用貝葉斯方法處理核電站PSA分析中的設備可靠性數據［A］．2004年全國機械可靠性學術交流會論文集［C］，2004．

［8］ 徐賓剛，屈梁生，陶肖明．轉子故障貝葉斯診斷網絡的研究［J］．機械工程學報，2004，40（1）：66-72．