19階Steiner三連系的構造與計數＊

鄭長波，李曉毅，侴萬禧

（1.大連海洋大學職業技術學院，遼寧大連 116300； 2.沈陽師范大學數學與系統科學學院，遼寧沈陽 110034；3.安徽理工大學土木建筑學院，安徽淮南 232001）

區組設計理論是組合數學的一個重要分支，它在試驗設計、競賽安排及數字通訊等許多領域中均具有重要作用.早在1850年，Kirkman提出了一個有趣的“15名女生”問題，并于同年做出解答［1－2］.1971年，D.R.Ray－Chaudhuri與R.M.Wilson共同發表論文《Kirkman女生問題的解》以闡明6n＋3階Kirkman三連系［3－4］.1961年，中國數學家陸家羲提出了BIBD設計可分解的充要條件［5－9］.在區組設計中，有一種稱為t－（v，k，λ）設計，是指由一個v元集X和X中某些k元子集（區組）族β所組成的序對，使得X中任意t元子集都恰含于λ個區組之中，當λ＝1，k＝3時稱為Steiner三連系.

1 基本思路

定義1 設CT（V，E）為完全圖Kv，若完全圖Kv中的v（v－1）／2個邊可排成上三角陣，使得Kv中的任意邊Vi，Vj分別與項Vi和項Vj關聯，則所得到的上三角陣就稱為邊矩陣，并記為.

v階Steiner三連系可視為完全圖Kv的v（v－1）／6個完全圖的K3的分解，若直接將完全圖Kv分解出v（v－1）／6個完全圖K3的困難極大，倘若將完全圖K3的邊矩陣先分解出若干個已存在的完全圖和若干個完全三分圖，再將各個完全圖分解出t（t－1）／6個完全圖K3，將各個完全三分圖分解出s×s個完全圖K3，所得到的全部完全圖K3就構成v階Steiner三連

系［2，10－12］.

命題1 設完全圖Kv的階數v≡1（mod 2）且（v－1）／2＝t，t為已存的Steiner三連系的階數，則v階Steiner三連系的構造等價于完全圖Kv的s＝t－1個t階完全圖，，…，和m＝t（t－1）／2個完全二分圖，，…，，或n＝t（t－2）／6個完全三分圖，，…，的分解，每個完全三分圖＝∪∪.因為s＝t－1個完全圖，，…，為v階Steiner三連系貢獻s×t（t－1）／2個完全圖K3，n＝t（t－2）／6個完全三分圖為v階Steiner三連系貢獻s×s×t（t－1）／2個完全圖K3，全部v（v－1）／6個完全圖K3恰好是v階Steiner三連系的v（v－1）／6個區組［13－15］.

2 19階Steiner三連系

2.1 構造方案A

按照方案A構造19階Steiner三連系的具體步驟是：

Step 1：將完全圖K19的19×18／2＝171個邊排成上三角陣，使得任意邊Vi，Vj分別與項Vi和項Vj關聯，得邊矩陣.

Step 4：讓t（t－1）／6＝12個2×2的三連系矩陣中的t（t－1）／6×2×2＝48個完全圖K3與，，…，構成1個19階Steiner三連系ST（19）：

2.2 構造方案B

按照構造方案B進行19階Steiner三連系構造的具體步驟是：

Step 1：同上；

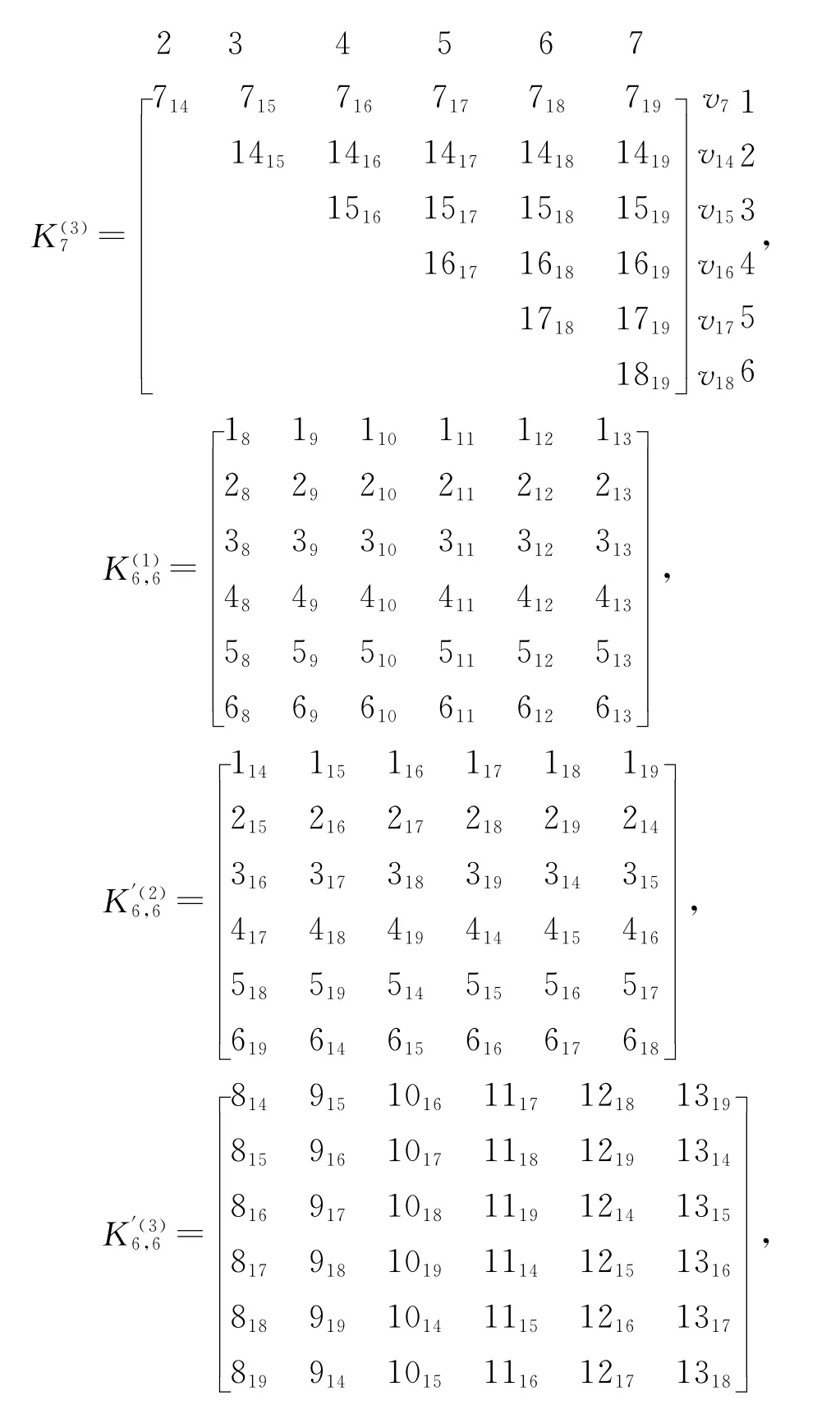
Step 4：將（v－1）／（t－1）＝3個t＝7階完全圖，，各分解出7個完全圖K3，得3×7＝21個完全圖K3.

3 結 語

基于邊矩陣的子矩陣分解的Steiner三連系的構造方法，適用于v≡1（mod t）的v階Steiner三連系的構造.構造結果表明：v元集X上的每個元素恰好出現于r個區組中；X的每兩個元素恰好出現于λ個區間組中.若按方案A構造Steiner三連系，Steiner三連系的個數NA決定于19階Steiner三連系的個數N1＝9和完全三分圖的三連系邊矩陣的完全圖K3的分解方案數N2＝2，故NA＝N1×N2＝14.若按方案B構造Steiner三連系，Steiner三連系的個數NB決定于3個7階Steiner三連系的完全圖K3的分解方案數＝7及完全二分圖的6×6個完全圖K3的分解方案數＝6，即有NB＝×＝42.Steiner三連系的總數可達N＝NA＋NB＝56個.

綜上，文中的Steiner三連系的構造方法和計數方法是有效可行的，對Steiner三連系的構造方法和計數方法具有一定的參考價值和可推廣性.

［1］ VAN LINT J H，WILSON R M.A course in combinatorics［M］.Beijing：China Machine Press，2004.

［2］ ROBERTS F S，TESMAN B.Applied combinatorics［M］.Beijing：China Machine Press，2007.

［3］ WEST D B.Introduction to graph theory［M］.Beijing：China Machine Press，2004.

［4］ FOULDS L R.Graph theory applications［M］.New York：Springer－Verlag，1992.

［5］ 陸家羲.可分解平衡不完全區組設計的存在性理論［J］.數學學報，1984，27（4）：28－38.LU Jia－xi.Incomplete block design with biodegradable balance of existence theory［J］.Acta Mathematica Sinica，1984，27（4）：28－38.（In Chinese）

［6］ 康慶德.斯坦納和柯克曼三元系及大集問題［J］.自然雜志，1985，8（6）：61－67.KANG Qing－de.Steiner and Kirkman triple systems and set problem［J］.Nature Magazine，1985，8（6）：61－67.（In Chinese）

［7］ 徐道.Steiner分割問題的進一步探討［J］.數學通報，1995，45（1）：41－44.XU Dao.Further explore for Steiner segmentation problem［J］.Shuxue Tongbao，1995，45（1）：41－44.（In Chinese）

［8］ 羅見今.Steiner系若干課題研究的歷史回顧——陸家羲學術工作背景概述［J］.數學進展，1986，75（2）：175－184.LUO Jian－jin.Historical review of the Steiner system research—an overview of Jiayi Lu＇s academic background［J］.Advances in Mathematics，1986，75（2）：175－184.（In Chinese）

［9］ 吳利生.關于S（2，3，υ）的大集和RBIB的存在性問題——我國組合數學工作者陸家羲同志的貢獻［J］.數學研究與評論，1984，4（1）：151－154.WU Li－sheng.Existence problem for about set S（2，3，υ）and RBIB—the contribution of Chinese combinatorial mathematics workers Jiayi Lu Comrade［J］.Journal of Mathematical Research and Exposition，1984，4（1）：151－154.（In Chinese）

［10］張瑾，馬良.基于加權絕對值距離Steiner最優樹的選址問題［J］.數學的認識與實踐，2008，38（16）：80－84.ZHANG Jin，MA Liang.A location problem based on the weighted rectilinear Steiner minimal tree［J］.Mathematics in Practice and Theory，2008，38（16）：80－84.（In Chinese）

［11］越民義，程叢電.關于Steiner問題的一個注記——連接五點之最小網絡的一種尋優方案［J］.運籌學學報，2010，14（1）：1－14.YUE Min－yi，CHENG Cong－dian.A note on the Steiner problem—an approach to find the minimal network with five given points［J］.Or Transactions，2010，14（1）：1－14.（In Chinese）

［12］侴萬禧.r×t階Kirkman三連系構造的一種方法［J］.數學的實踐與認識，2004，34（9）：144－145.CHOU Wan－xi.A method of constructing Kirkman triple system of order r×t［J］.Mathematics in Practice and Theory，2004，34（9）：144－145.（In Chinese）

［13］侴萬禧.高階Steiner三連系及其構造方法［J］.安徽理工大學學報：自然科學版，2004，24（3）：76－80.CHOU Wan－xi.Steiner triple system and its construction method［J］.Journal of Anhui University of Science and Technology：Natural Science，2004，24（3）：76－80.（In Chinese）

［14］侴萬禧，李曉毅.完全圖K5中的生成樹的構造與計數［J］.沈陽師范大學學報：自然科學版，2010，28（3）：327－330.CHOU Wan－xi，LI Xiao－yi.Construction and counting of spanning tree in complete graph K5［J］.Journal of Shenyang Normal University：Natural Science Edition，2010，28（3）：327－330.（In Chinese）

［15］侴萬禧，李曉毅.49階Steiner三連系的構造與計數［J］.長春工業大學學報：自然科學版，2009，30（6）：623－628.CHOU Wan－xi，LI Xiao－yi.Construction and numeration of Steiner triple systems of order 49［J］.Journal of Changchun University of Technology：Natural Science Edition，2009，30（6）：623－628.（In Chinese）