基于Bayesian－MCMC方法的水體污染識別反問題＊

陳海洋，滕彥國，王金生，宋柳霆，周振瑤

（北京師范大學水科學研究院，北京 100875）

隨著我國經濟的快速發展，各種自然災害和人們的生產經營活動帶來的環境風險不斷加劇，突發性水體污染事件時有發生，給人民群眾的生命健康、財產安全和生態環境造成了巨大損失.迅速找出污染源位置、掌握其排放強度、了解事件發生的初始時間，對于開展污染應急處置具有重要的現實意義.然而事件發生時，這些信息往往是不確知的，也是不適定的.為此，需根據水體環境系統的自身特點，構建污染擴散對流控制方程，利用已有水文水質參數以及濃度場的部分信息，推求污染源位置、源強及事件發生初始時間，即為環境水力學反問題.

與已知水力水質參數推算污染物濃度的正問題不同，反問題通常會由于測量數據有限且帶有噪聲，使得污染源識別成為不適定問題［1］.常見的反演方法有正則化方法［2］、優化算法［3］、數值法［4］和統計反演法［5］等.其中建立在貝葉斯統計學基礎上的貝葉斯推理能以概率語言來描述和解決工程反問題，可以較好地用來實現污染源識別反問題的求解［6］.

當前，環境水力學反問題研究尚處于起步階段，研究成果不多，且以參數反演居多，部分源項識別研究以數學方法證明為主，對模型邊界條件、初始條件假設過于嚴格［7］.本文基于貝葉斯推理和二維水質擴散對流模型，考慮有限寬度河流的瞬時岸邊污染泄漏，建立水體污染識別數學模型，以典型Metropolis算法構建馬爾科夫鏈，取得污染泄漏源源強、泄漏位置和污染泄漏初始時間3個模型參數后驗概率分布，并通過基于混合遺傳模式搜索算法的求解結果進行比較，分析MCMC－Bayes方法的識別效果.

1 正問題

一個考慮二維水質對流擴散方程可以表述為：

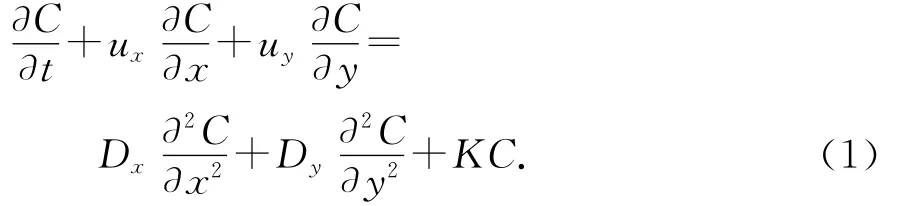
式中：C為（x，y，t）處的污染物質量濃度，mg／L；ux和uy分別為河流縱向和橫向的流速分量，m／s；Dx和Dy分別為河流縱向和橫向的混合系數，m2／s；K為污染物降解系數，d－1.

對于瞬時點源排放，方程解析解可表示為：

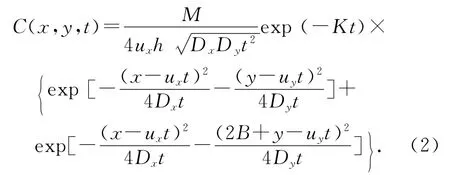
式中：h為河流深度；M為污染物排放量，g／s；B為點源到邊界的距離，m；其他同上.如在岸邊排放，則B＝0，有：

2 基于MCMC－Bayes方法的污染識別反問題

2.1 貝葉斯推理

貝葉斯推理基于如下貝葉斯公式：

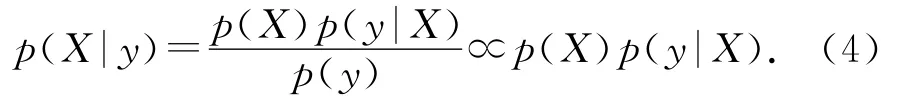
式中：p（X｜y）為參數的后驗概率密度函數；X為模型參數；y為觀測數據；p（X）為參數的先驗概率密度函數；p（y｜X）為條件概率密度；p（y）為積分常數.

通常，環境水力學的模型參數都分布在一個特定的范圍內，滿足獨立的均勻分布，其先驗概率密度函數可定義為：

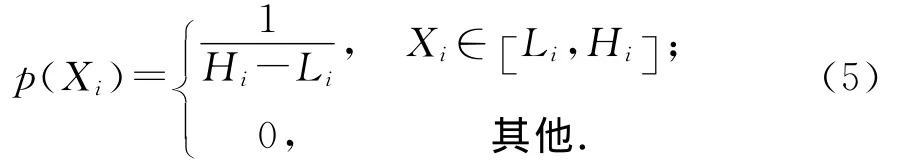
則總的先驗分布可表示為：

而污染物濃度場的測量噪聲一般可以認為是白噪聲，其誤差服從均值為零、標準偏差為σ的正態分布，ε～N（0，σ2），條件概率密度定義為：

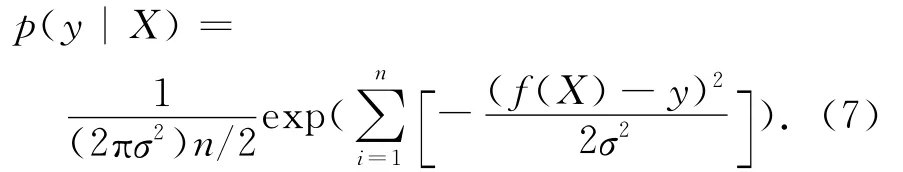
式中：n為測量數據個數.

把式（6）～（7）代入式（4），并把分母表示的常數項正規化為1可得：

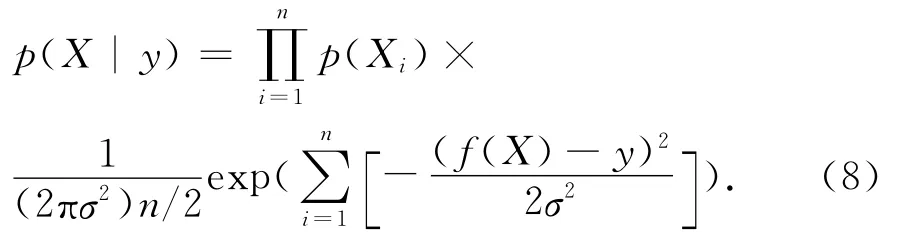
理論上，利用式（8）可以獲得任何環境模型參量的統計矩，但事實上，后驗概率密度的求解算法較為復雜，難以得出明確的解析表達式.另一方面，隨未知參量維數的增加，數值積分算法的計算量將呈指數增長，實現復雜而難度較大.為此，需要采取其他改進的方法以實現后驗概率密度的求解.

2.2 馬爾科夫鏈蒙特卡羅法

馬爾科夫鏈蒙特卡羅法（Markov Chain Monte Carlo，簡稱MCMC）是近期發展起來、可很好地用來求解貝葉斯后驗概率密度的統計方法.其基本思想是對定義在高維隨機向量空間的無明確數學表達式的概率分布p進行抽樣，產生大量服從分布p的隨機向量序列，通過建立合適的抽樣算法使得該序列滿足馬爾科夫鏈性質，以保證向量Vi＋1的產生僅依賴于向量Vi，而與Vi－1，Vi－2，…，V1等向量無關.這樣，抽樣算法完全可以由轉移概率矩陣P來描述，矩陣元素pij表示當前訪問向量Vj的條件下接著將要訪問Vi的條件概率［8］.

可見，MCMC方法利用Markov鏈機制探索狀態空間以生成樣本的方法能夠保證Markov鏈花更多的時間在最重要的區域，產生的樣本更能夠模仿目標分布樣本.常見的構造Markov鏈轉移概率矩陣的方法有Gibbs抽樣算法、Metropolis－Hastings算法、Metropolis算法和自適應Metropolis算法等.本研究采用Metropolis算法.

2.3 Metropolis算法

Metropolis是Metropolis－Hastings算法的特例，其Proposal分布函數滿足對稱隨機游走，即q（X＊｜X（i））＝q（X（i）｜X＊）.從當前位置X（i）獲得候選抽樣值X＊，Markov鏈從X（i）位置移動到X＊的接受概率為［9］：

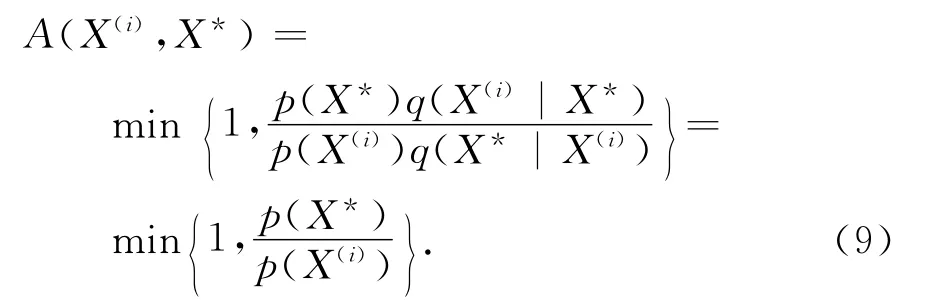
式中：p（X＊），p（X（i））為目標概率密度函數，在貝葉斯推理中為條件概率密度.

2.4 基于Metropolis算法的反演思路

1）在模型參數先驗范圍內隨機產生模型參數初始點X（i）（i＝1）；

2）利用水質模型計算出模型參數初始點對應的污染物濃度值，并計算出該模型參數對應的條件概率密度L＿MODEL；

3）根據Proposal分布在當前參數X（i）狀態下提取新的測試參數X（＊），利用水質模型計算出測試參數X（＊）對應的污染物濃度及條件概率密度L＿TEST；

4）產生一個0～1之間的隨機數u，如果u＜min（1，L＿TEST／L＿MODEL），則接受該測試參數并設定為當前模型參數，即X（i＋1）＝X（＊），否則不接受該測試參數，X（i＋1）＝X（i）；

5）重復步驟3），4）直至達到迭代次數.

3 實例與討論

模擬案例假定如下：某河段斷面A上游發現污染帶前鋒，經檢測污染物為B危險化學品，現需利用斷面A帶噪聲的濃度場部分分布數據反演上游污染泄漏源位置、初始泄漏時間及泄漏強度.假定該河流河段均勻，河流水文條件穩定，河段斷面積、平均流速穩定，滿足二維水質模型應用條件，污染排放為岸邊瞬時泄漏，相關參數及先驗信息見表1；A斷面污染物濃度監測數據見圖1；初始監測時間為發現污染帶后的第一時間，某日下午15時，后每隔30 min監測一次，直至當日下午19時.

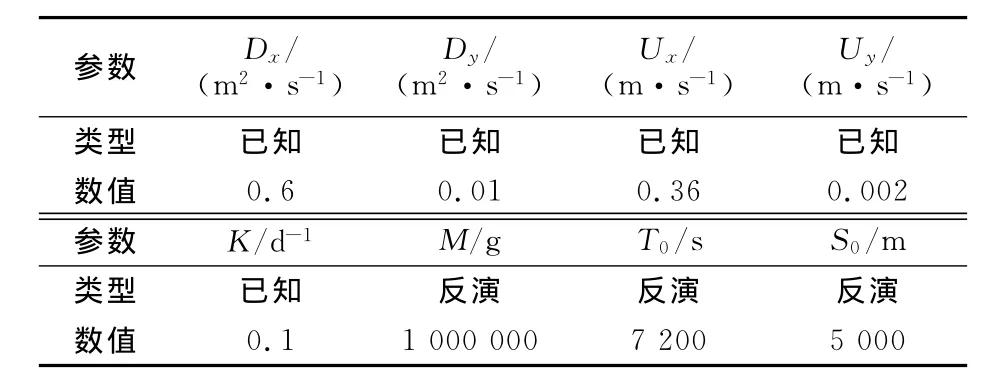
表1 某河流斷面水文水質參數Tab.1 Model parameters of study area

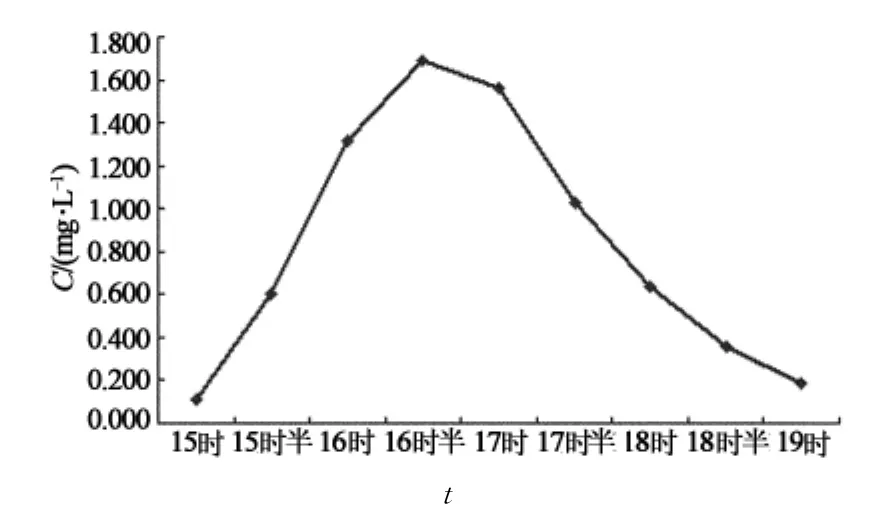
圖1 斷面A污染物觀測濃度序列Fig.1 Simulation observe concentration serial of site A

3.1 反演分析

假定污染物從岸邊瞬間排入河道，泄漏量為M，泄漏地點距離A斷面S0，泄漏時間距離首次監測時間為T0，參數“真值”見表1.利用表1中的3個模型參數真值及其他參數計算出斷面A的污染物濃度分布，初始監測時間為發現污染帶后的第一時間，某日下午15時，后每隔30min監測一次，直至當日下午19時，見圖1.

從圖1可以看出，9組A斷面污染物濃度序列近似正態分布，最高值發生于該日16時30分，污染物質量濃度達到1.62mg／L，到19時已經降低為0.19 mg／L.據先驗信息，該突發污染事故可能為交通事故導致的污染物泄漏或化學品企業儲罐爆炸泄漏瞬間排入河流造成的污染.

設坐標中心為污染源泄漏點，測點A坐標為（S0，0），待反演參數定義為X（M，S0，T0）.根據先驗信息，3個待反演模型參數先驗分布為均勻分布，其對應的先驗概率密度函數分別為：

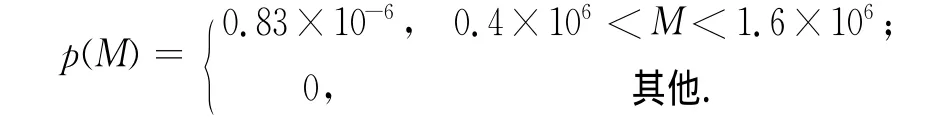
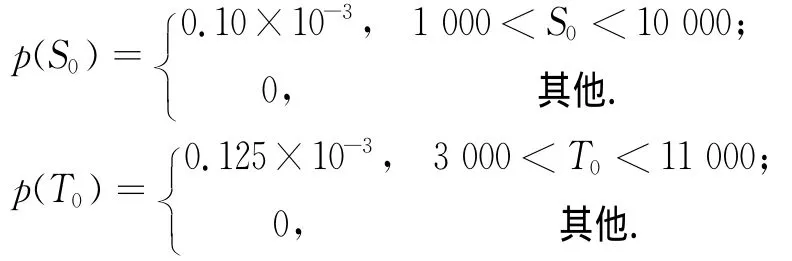
假定觀測誤差為白噪聲N（0，σ2），σ＝0.01，條件概率密度表示為：

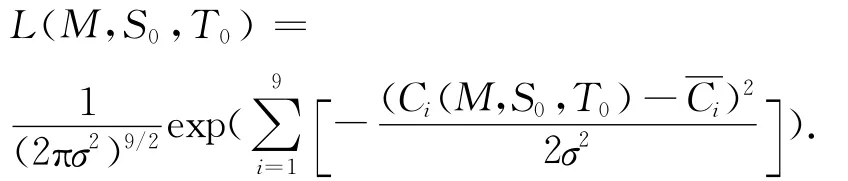
根據貝葉斯定理，模型參數的后驗概率密度函數為：

式中：λ為一比例常數.

3.2 反演結果

取Proposal分布為均勻分布q（X＊｜X（i））＝U（X（i）－ΔX，X（i）＋ΔX），步長為先驗范圍的5%，取ΔX（M，S0，T0）＝（60 000，450，400），按照Metropolis算法反演思路迭代10 000次.3個參數的迭代曲線見圖2，參數后驗概率直方圖見圖3.

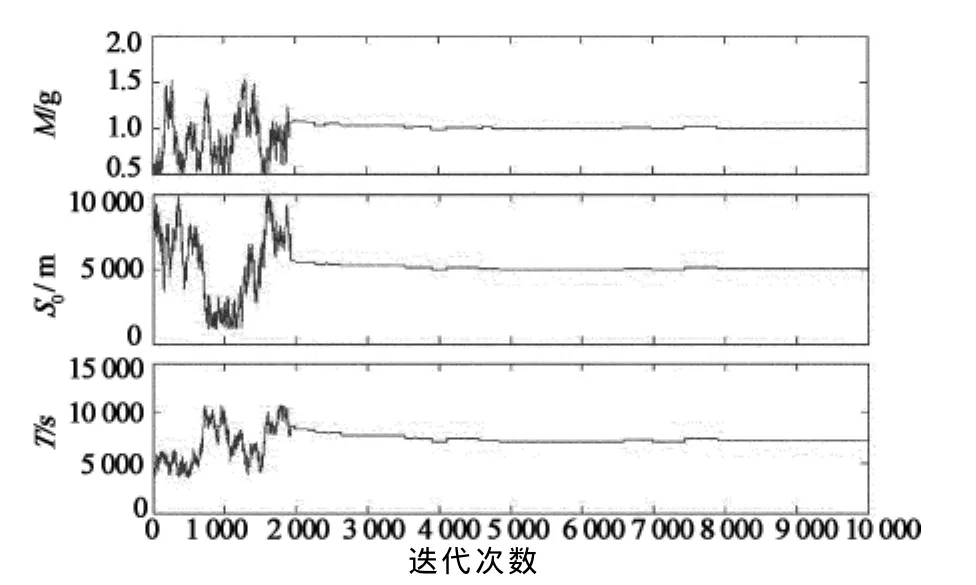
圖2 參數反演迭代曲線Fig.2 Iteration curve of model parameters

從圖2可看出，迭代約2 000次后，M，S0，T0均達到穩定，馬爾科夫鏈進入穩定收斂區域.從圖3可看出，3個模型參數后驗概率密度呈現不太明顯的正態分布；污染源源強M在1 000 000g附近的頻度最大，完全符合預定設定初值；污染源距離A斷面距離S0在5 000m附近的頻度最大，與預先設定值完全符合；而污染泄漏時間距A斷面首次監測時間T0在7 000～8 000s區間頻度最大，與預先設定值較為接近.

圖3 參數后驗概率直方圖Fig.3 Posterior histogram of model parameters

3.3 反演效果分析

為進一步驗證反演結果，剔除前面2 000次結果，對其他8 000次模型參數進行后驗統計分析，分析結果見表2.可以看出，3個參數的數學期望誤差、中值誤差均較小，而以污染源強度M的誤差最小.

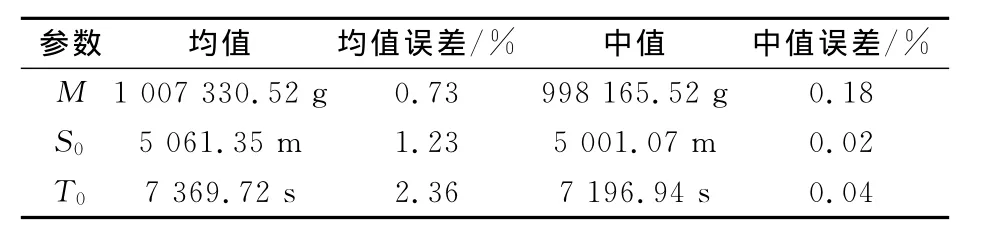
表2 污染源參數后驗統計結果Tab.2 Posterior statistical results of model parameters

為了檢查基于MCMC－Bayes方法的反演穩定性，采取多次間隔性反演提取模型參數反演誤差序列，見圖4.可以看出，反演結果較穩定，3個參數的相對誤差均在9%以內，平均誤差分別為2.94%，2.50%和2.21%.比較而言，污染源源強M的誤差起伏較大，位于［0.48%，8.48%］；污染源位置S0的誤差起伏次之，位于［2.50%，5.90%］；污染源泄漏時間T0的誤差起伏最小，位于［2.21%，4.65%］.

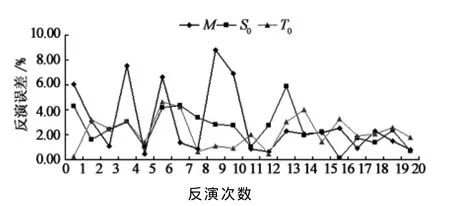
圖4 基于MCMC－Bayes問題反演誤差分析Fig.4 Error serial with method of MCMC－Bayes

作為比較，本文采用混合遺傳模式搜索算法對該問題進行求解，反演誤差見圖5.可以看出，采用混合遺傳模式搜索算法求解的問題解誤差較大，最高誤差達到24.7%，3個參數的平均誤差分別達到3.20%，4.08%，7.45%.其中污染源泄漏時間T0的誤差起伏最大，位于［1.21%，24.7%］；污染源源強M的誤差起伏次之，位于［0.54%，10.69%］；污染源位置S0的誤差起伏最小，位于［0.68%，13.33%］.

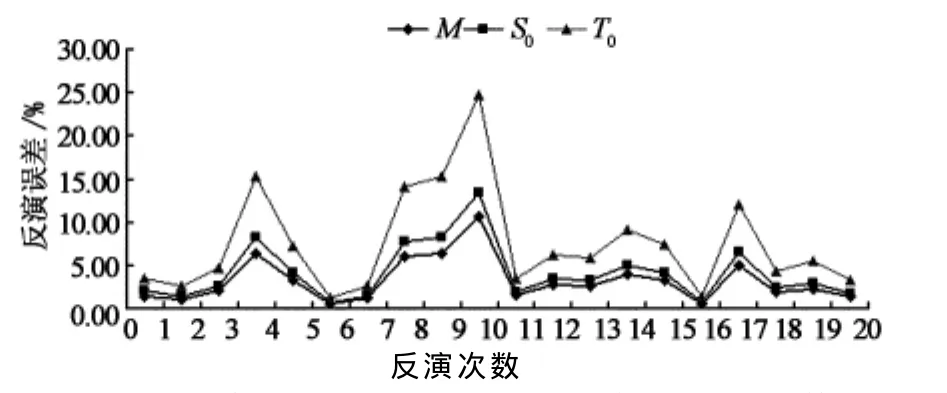
圖5基于混合遺傳模式搜索算法的問題反演誤差分析Fig.5 Error serial with method of hybrid GA－Patter search

兩種方法反演的模型參數誤差比較見表3.很明顯，基于MCMC－Bayes的源識別誤差遠小于優化算法，3個參數的最小誤差、最大誤差和平均誤差都呈現明顯的特征，可見，相對優化算法而言，基于MCMC－Bayes的源識別方法具有良好的可靠性和穩定性.

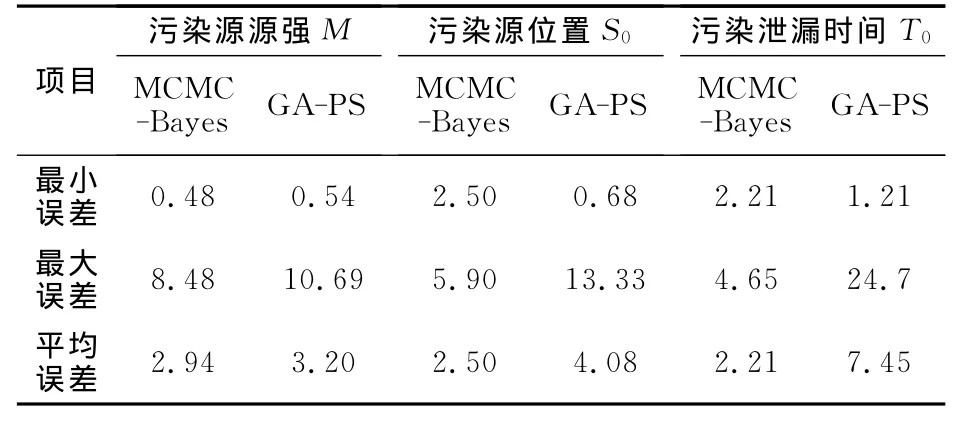
表3 基于MCMC－Bayes 和混合遺傳模式搜索算法（GA－PS）的反演誤差對照Tab.3 Error comparison with method of MCMC－Bayes and GA－PS%

4 結 論

污染源識別對于開展突發污染事故應急處置、加強水質管理和控制具有重要的現實意義，而由于測量數據有限且帶有噪聲等原因使得污染源識別成為一個不適定問題.本研究基于貝葉斯推理和二維水質模型建立水體污染識別數學模型，運用馬爾科夫鏈蒙特卡羅法抽樣獲得了污染源源強、污染源位置和污染泄漏時間3個模型參數的后驗概率分布和統計結果.實例研究結果表明，基于馬爾科夫鏈蒙特卡羅抽樣算法的貝葉斯推理可以較好地用來實現水體污染識別，具有識別精度高、誤差小的特點，其可靠性和穩定性高于混合遺傳模式搜索優化算法.

總體看來，MCMC－Bayes通過構造Markov鏈進行隨機動態模擬，實現對高維空間無明確數學表達式概率分布密度函數的數值計算，且具備計算速度快、復雜度不依賴于計算空間維數等特點.同時，它可以方便地將各種先驗信息和誤差信息高效地融合到問題求解過程中，減小問題的不確定性，獲得全局最可能解，可以很好地用來開展同屬問題不適定的水體污染反問題研究.

［1］ 戴會超，王玲玲.工程水力學反問題研究及應用［J］.四川大學學報：工程科學版，2006，38（1）：15－19.DAI Hui－chao，WANG Ling－ling.Study and application of the inverse problem on hydraulics［J］.Journal of Sichuan University：Engineering Science Edition，2006，38（1）：15－19.（In Chinese）

［2］ 劉繼軍.不適定問題的正則化方法及應用［M］.北京：科學出版社，2005：42－46.LIU Ji－jun.Regularization methods of ill－posed problems and its application［M］.Beijing：Science Press，2005：42－46.（In Chinese）

［3］ 閔濤，周孝德，張世梅，等.對流擴散方程源項識別反問題的遺傳算法［J］.水動力學研究與進展，A輯，2004，19（4）：520－524.MIN Tao，ZHOU Xiao－de，ZHANG Shi－mei，et al.Genetic algorithm to an inverse problem of source term identification for convection－diffusion equation［J］.Journal of Hydrodynamic Ser A，2004，19（4）：520－524.（In Chinese）

［4］ 王澤文，邱淑芳.一類流域點污染源識別的穩定性與數值模擬［J］.水動力學研究與進展，A輯，2008，23（4）：364－371.WANG Ze－wen，QIU Shu－fang.Stability and numerical simulation of pollution point source identification in a watershed［J］.Journal of Hydrodynamic Ser A，2008，23（4）：364－371.（In Chinese）

［5］ 嚴齊斌.河流水質參數估計的蒙特卡羅方法［J］.水利水電技術，2006，37（10）：14－16.YAN Qi－bin.Monte Carlo method for estimation on parameters of river water quality［J］.Water Resources and Hydropower Engineering，2006，37（10）：14－16.（In Chinese）

［6］ 朱嵩，劉國華，毛根海，等.利用貝葉斯推理估計二維含源對流擴散方程參數［J］.四川大學學報：工程科學版，2008，40（2）：38－43.ZHU Song，LIU Guo－hua，MAO Geng－hai，et al.Application of Bayesian inference to estimate the parameters in 2Dconvection－diffusion equation with source［J］.Journal of Sichuan University：Engineering Science Edition，2008，40（2）：38－43.（In Chinese）

［7］ 劉曉東，姚琪，薛紅琴，等.環境水力學反問題研究進展［J］.水科學進展，2009，20（6）：885－890.LIU Xiao－dong，YAO Qi，XUE Hong－qin，et al.Advance in inverse problems of environmental hydraulics［J］.Advance in Water Science，2009，20（6）：885－890.（In Chinese）

［8］ 曹小群，宋君強，張衛民，等.對流擴散方程源項識別反問題的MCMC方法［J］.水動力學研究與進展，A輯，2010，25（2）：129－135.CAO Xiao－qun，SONG Jun－qiang，ZHANG Wei－min，et al.MCMC method on an inverse problem of source term identification for convection－diffusion equation［J］.Journal of Hydrodynamic Ser A，2010，25（2）：129－135.（In Chinese）

［9］ ANDRIEU C，FREITAS N D，DOUCET A，et al.An introduction to MCMC for machine learning［J］.Machine Learning，2003，50：5－43.