空時交織碼

2012-03-19 08:22:20李道本

北京航空航天大學學報 2012年8期

孫鵬李道本

(北京郵電大學信息與通信工程學院，北京 100876)

移動通信中信道傳輸條件較為惡劣，發送端傳輸信號通常經歷嚴重衰落才能到達接收端，接收信號的質量和信息判決的精確率都會劇烈下降.無線傳播環境中，調制信號經歷復雜的傳輸路徑，從而在時間上形成擴散，即多徑.由于信號在時間上的擴散導致了頻率上的選擇性衰落，多徑衰落信道也被稱為頻率選擇性信道.盡管多徑信道會引入符號間干擾等問題，但假如不同徑的衰落因子相關性較弱，則該多徑信道可提供頻率分集增益，如加以合理利用，頻選信道性能將遠高于單徑瑞利衰落信道性能.文獻［1］證明了隨著多徑數的增加，系統的性能會逐漸逼近AWGN(Ad-ditive white Gaussian Noise)信道的性能.

多天線的出現則從空間的角度提供了另一維度的分集增益，合理設計發送信號可大幅度提升系統性能，3GPP已經在WCDMA系統中使用了著名的Alamouti方案［2］.近十幾年來，已經有多種多樣的空時碼字提出［2－7］，但大部分的空時碼字均是為單徑瑞利衰落信道，而未考慮頻率選擇性信道.實際上，多天線系統的頻率選擇性信道提供了更多重的分集增益，假如通過合理設計利用該部分分集增益，則系統性能將大幅度提升.LTE等系統中的空頻碼(space frequency block codes)通過時頻轉換，直接消除了多徑，從而簡化了系統設計.但該方法需要以OFDM(Orthogonal Frequency Division Multiplexing)技術為基礎，在一些OFDM不適用的場合，比如一些對峰均比(peak to average power ratio)、移動性、抗干擾性要求較高的系統，該方法就不適合使用.此外，空頻碼還依賴較強的信道編碼獲得相應分集增益，當譜效率增加，信道編碼碼率增高時，系統便不能獲得分集增益.因此考慮一般的頻率選擇性信道中空時碼的設計還有很大的意義.

正交的空時碼［3－4］可在平坦衰落信道中獲得滿發分集，但在頻選信道中并不能完全利用信道提供的分集.此外，正交空時碼還存在碼率損失.當天線數大于2時，對于復星座圖不存在滿分集滿速率方案.廣義延遲分集GDD(Generalized Delay Diversity)［5］是針對頻選信道的主要設計之一，該方案可獲得完整的頻率分集與空間分集增益.但是隨著天線數增加，該方案接收機復雜度指數上升，對系統實現構成了挑戰.文獻［5］中的簡化預編碼方案實際是利用IFFT進行時頻變換，因此該方案與空頻編碼面臨同樣的問題.文獻［6］將Alamouti方案推廣至多徑信道中，但該方案同樣存在碼率損失.其他滿分集滿速率方案還有TAST(Threaded Algebraic Space-Time Coding)［7］，該方案的問題則在于接收端復雜度較高，盡管可通過球譯碼降低，但實際使用中仍然復雜度較高.利用自相關、互相關特性在多徑范圍內理想的零相關窗碼［8－9］也可設計出相應的方案，但譜效率較低，存在速率損失.

本文提出的空時交織碼可在多徑信道中獲得滿分集，并進行滿速率傳輸.該方案通過在不同的天線上設置隨機交織器獲得相應的頻率及空間分集增益，因此可應用于任意多根天線.此外，交織器的存在還便于將接收機設計為迭代結構，大幅度簡化最優檢測的復雜度.仿真結果顯示，系統BER(Bit Error Rate)性能在4～5次迭代內便可收斂至理想分集增益曲線，而其復雜度僅僅隨發端天線數線性增長.

本文首先介紹系統模型，并給出多徑信道下空時碼設計的準則.其次給出空時交織碼方案及迭代接收機設計方法.最后給出仿真結果及結論.文中各符號含義如下:(·)T表示·的轉置;H(i，j)表示矩陣H的第i行、第j列元素;h(i)表示向量h的第i個元素;h［m］表示時變向量h在m時刻的值.

1 系統模型及設計準則

本文主要考慮發端有Nt根天線，收端有1根天線的多入單出(MISO，Multi-Input Single-Output)的系統(但實際上本文所設計方案非常容易推廣到多接收天線系統).MISO系統中一般只考慮單碼流，該碼流經過調制及空時編碼從Nt根天線上發射出去.

對于準靜態頻選MISO信道來說，其等效基帶模型可表示為

其中，y［m］表示時刻m的等效基帶輸出;si［ml］表示第i根天線在 m －l時刻的發送信號;hi［l］表示第i根天線與接收天線間多徑信道的第l徑.本文假設所有Nt根發送天線與接收天線間的多徑抽頭數目均為L，并且各天線各抽頭間分布獨立.該模型可表示為向量形式:

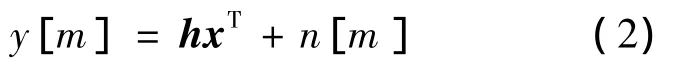
其中

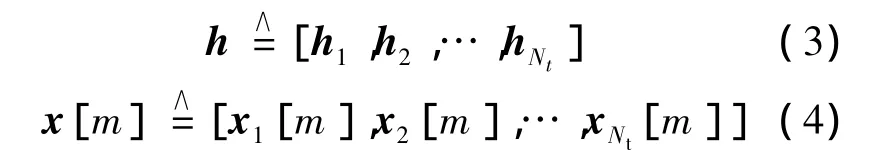
以及

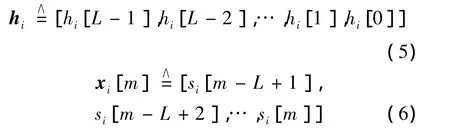
為便于分析，將M個接收符號作為一幀處理，并且前后幀間間隔足夠隔離多徑影響.定義如下符號向量及矩陣:

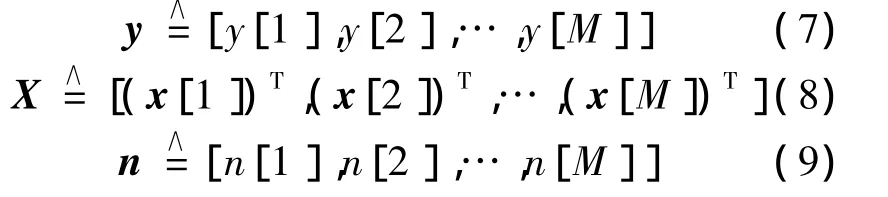
則系統模型可表示如下:

從該模型可看出，Nt根發送天線的頻選MISO信道可看作是有NtL根虛擬發射天線，且發送信號按式(8)重組的單徑MISO信道.因此單徑信道空時塊碼的滿秩準則可推廣到多徑信道下空時塊碼的設計.對一預先設計好的空時碼，假如發送信號按式(8)重組后的任意兩個碼字 X(1)和X(2)，其碼字差矩陣Xdiff=X(1)－X(2)行滿秩，則經接收端最大似然檢測便可獲得滿分集，即NtL重分集.需注意在式(6)、式(8)以及式(10)中，代表時間的變量可能取值為負，這些時刻的各變量取值均設為0，表示在0時刻之前沒有信號傳輸.利用該準則可檢查GDD方案.由于天線間的信號有相互L徑的延時，因此可以很容易確定按式(8)重組后的碼字滿足行滿秩準字.因此GDD可以實現滿分集.

2 空時交織碼發射機

空時交織碼發射機由同一數據流在不同的天線上進行不同的交織得到，其結構如圖1所示.

本文以2根發送天線，2個多徑抽頭為例說明該設計的有效性.假設發送的調制符號數據流如下:

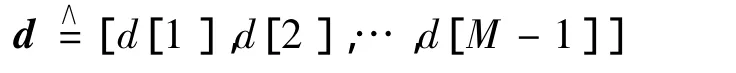
兩根發天線處的隨機交織器分別為

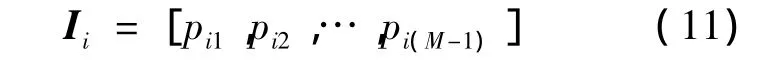
其中pij表示天線i處交織器交織前位置.因此天線i上交織后的數據為

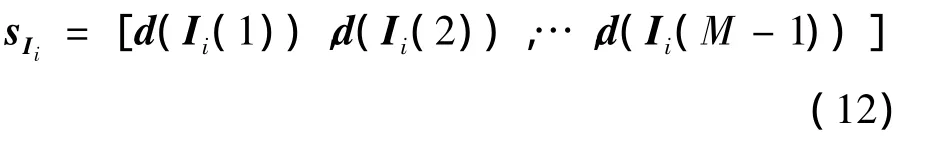
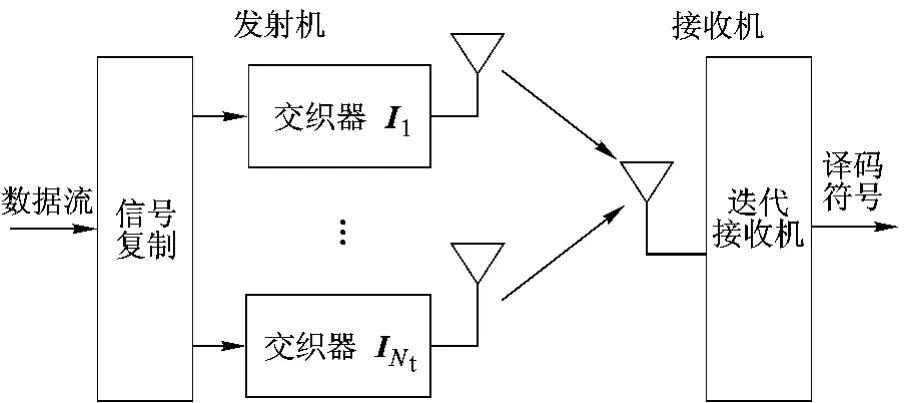
圖1 空時交織碼系統結構框圖

因此兩天線上傳輸數據為

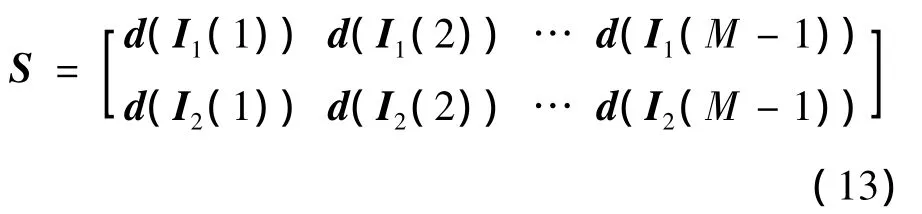
按照式(8)重組可得

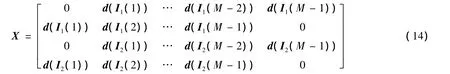
假如系統中未使用信道編碼，對應碼字差矩陣秩最小的調制符號數據流為僅有一個調制符號不同的兩組數據向量.為簡便起見，不妨設該不同的調制符號是經天線1處交織器交織后數據向量的第一個，即

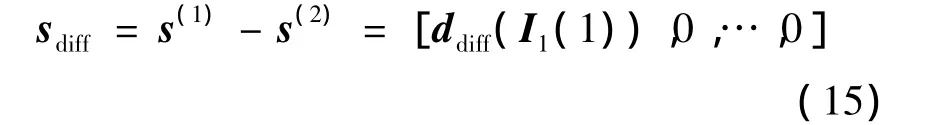
因此重組后的碼字差矩陣為

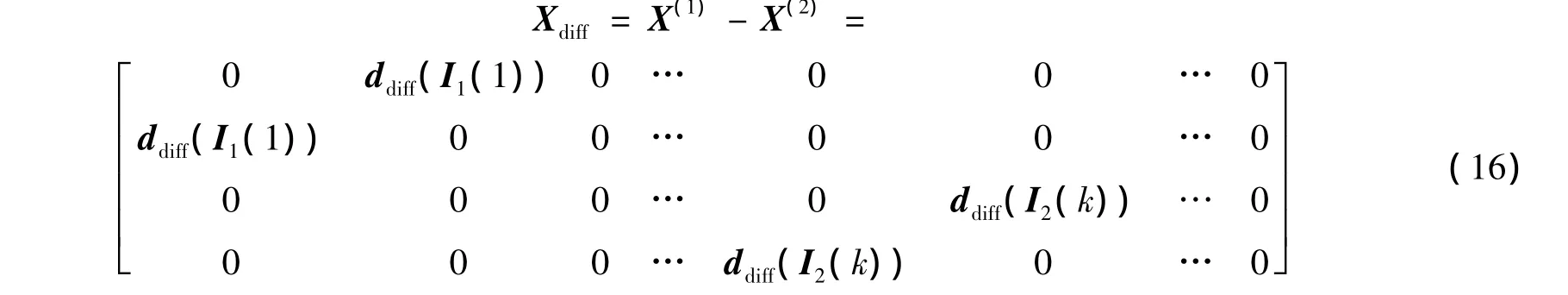
其中

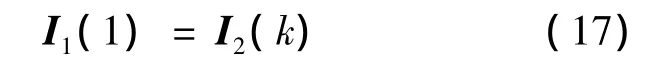
即兩交織器分別將原數據流中同一位置的數據交織到位置1處和位置k處.

假如交織器設計合理，可證明碼字差矩陣(16)將滿足行滿秩條件.比如，兩天線條件下，S隨機交織器將是非常好的選擇.該交織器可將一個符號交織到距離之前位置至少一定距離以外，因此式(16)必然滿足行滿秩.當天線數大于2時，合理設計的行列交織器將滿足相應條件.盡管交織器設計看起來比較復雜，但實際上只要數據流長度足夠，則在各天線處選擇隨機交織器幾乎以概率1滿足行滿秩條件.因為對隨機交織器來說，產生的隨機位置在某范圍之內的概率非常小.本文的仿真結果即可證明利用隨機交織器進行信號傳輸已經能夠獲得非常接近理想性能的結果.

3 空時交織碼迭代接收機

空時交織碼的最大似然檢測如下:

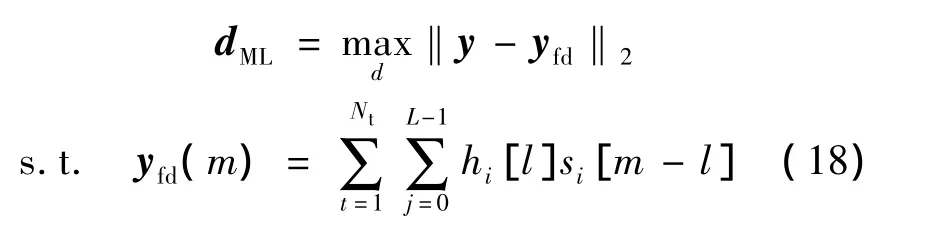
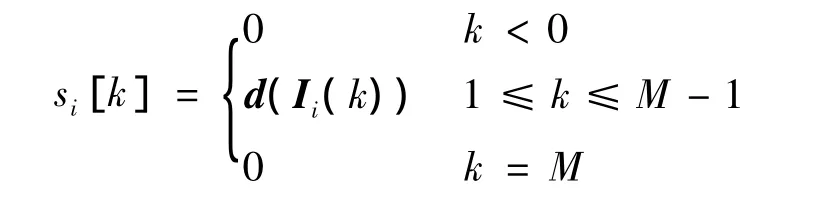
其中，y表示等效基帶輸出;yfd表示在調制符號數據流為d時接收端未受噪聲干擾的衰落信號;si表示天線i處的發送信號.為獲得滿足上述條件的最優d，整個序列空間都要進行搜索，這一復雜度隨序列d的長度指數增長.應當注意到，由于交織器打亂了序列d前后約束關系，維特比算法(VA)并不能在該求解中應用.而在GDD接收機中，由于天線間L符號的延遲可等效為相應的信道延遲，因而可利用抽頭為NtL的VA算法求解.盡管相比式(18)，該復雜度可大幅度降低，但其仍然隨天線數增加指數增長.

在空時交織碼方案中，由于交織器的存在，可以將式(18)中復雜的最大似然接收機分解為若干個軟入軟出(SISO，Soft Input Soft Output)模塊，通過在這些模塊之間進行軟信息的迭代，可逐漸逼近最大似然檢測.可以看到一方面多個天線上的數據是由同一數據流交織得到，因此某些元素相互間滿足相等的約束關系;另一方面，多個天線上的數據經過多徑信道實際形成了(Nt，1)的卷積約束關系.因此，數據可在這兩個約束關系間進行迭代.由于卷積約束關系實際可看作一系列校驗關系的串聯，即在當前狀態、輸入信號、下一狀態、輸出信號間形成校驗約束，因此最終的迭代結構實際上是在一組校驗約束與一組相等約束間進行迭代，這與(LDPC，Low Density Parity Check)碼譯碼器在校驗節點與變量節點間迭代非常相似.

上述(Nt，1)的卷積約束關系仍然較為復雜，其復雜度隨天線數增加依然指數上升.因此須對該約束關系進行進一步分解.由于多個天線的數據在到達接收天線前各自經歷多徑衰落，該(Nt，1)的卷積約束關系可進一步分解為Nt個碼率為1的卷積關系的疊加，從而軟信息可在疊加的約束關系與Nt個卷積關系間進行迭代.將利用疊加約束關系進行軟入軟出譯碼的模塊稱為解加器(desummer)，其外信息(extrinsic information)計算式為

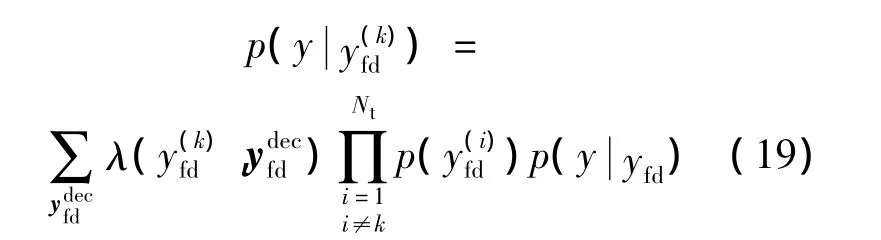
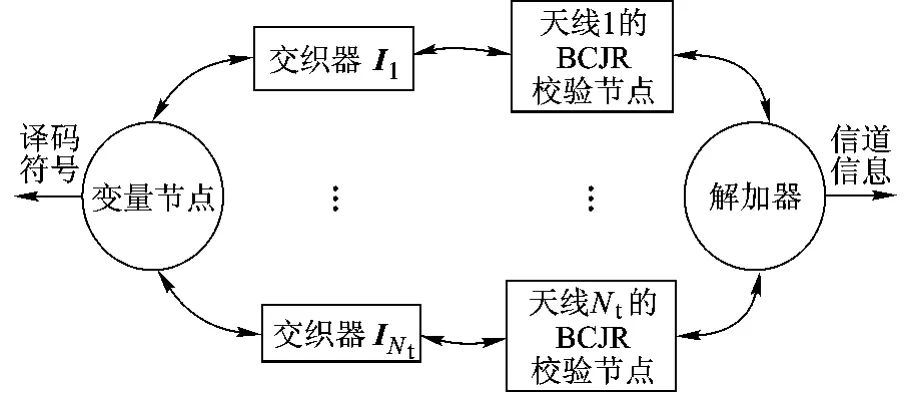
圖2 分布式BCJR迭代接收機整體結構圖

4 仿真結果

本節通過仿真給出空時交織碼及不同接收機結構的系統性能.仿真中各天線各抽頭獨立同分布，即均服從復高斯分布.仿真中天線數目基本限定在2～8.

首先對空時交織碼在頻選信道中的有效性進行仿真.發天線數目分別被設置為2，4及8，抽頭數量均被設置為2.因此信道提供的多徑數量分別為4，8及16.數據流采用 BPSK(Binary Phase Shift Keying)調制.各天線上的交織器為獨立生成的隨機交織器.接收端采用了圖2所示迭代結構，迭代次數為5次.仿真結果在圖3中列出.從結果中可看出，該方案性能非常接近理想性能曲線.盡管隨著天線數的增加，性能相比理想曲線略有損失，但是可以看到該損失幾乎可以忽略不計.此外，盡管由于最大似然檢測復雜度非常高而未給出性能，但其應當介于迭代檢測與理想分集曲線之間，而仿真顯示迭代檢測非常接近理想分集曲線，因此最大似然亦應當非常接近理想分集曲線.這也顯示迭代檢測幾乎沒有性能損失.同時可見，盡管各天線處采用隨機交織器，系統仍然能獲得完整的分集增益.

本文還對不同迭代結構性能進行了對比，一種是直接在(Nt，1)的卷積約束關系與相等關系間進行迭代，稱之為聯合BCJR(joint BCJR)算法，另一種是圖2所示迭代結構，稱為分解BCJR(decomposed BCJR)算法.仿真中發端天線數為2，多徑抽頭數為3，仿真各次迭代性能如圖4所示.從圖中可以看出，盡管聯合BCJR算法第一次迭代性能大大優于分解BCJR算法，但隨著迭代次數的增加，兩個算法間的差距越來越小，最終都收斂于理想分集曲線附近.

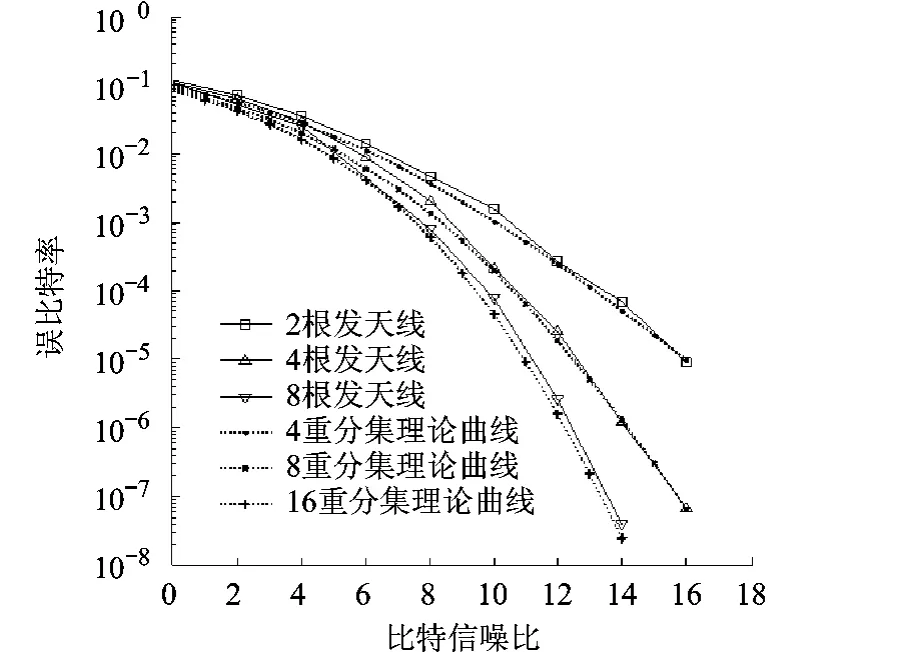
圖3 空時交織碼與理想分集曲線性能比較

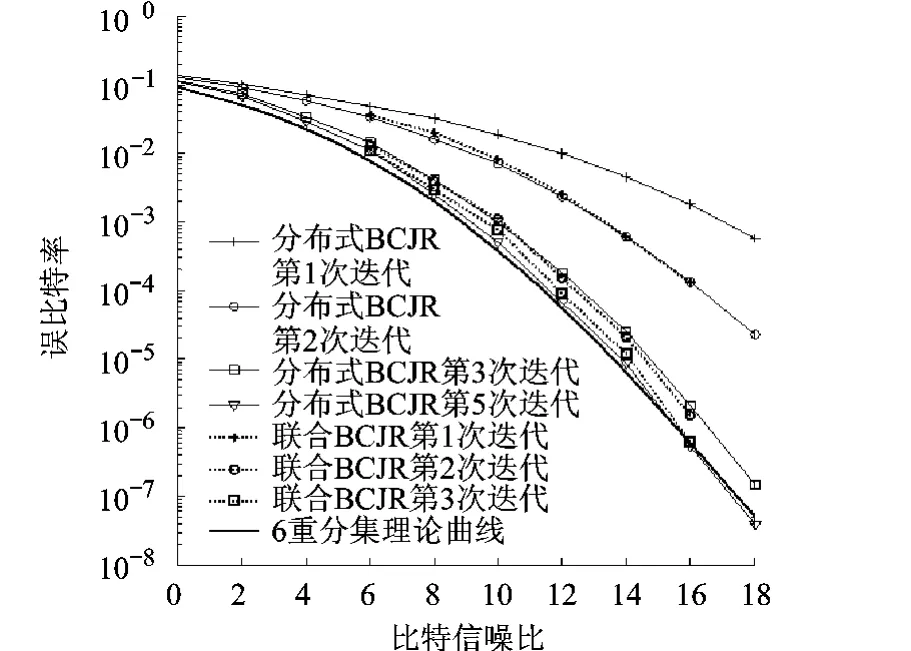
圖4 聯合BCJR與分布式BCJR迭代接收機性能比較

5 結束語

綜上所述，本文提出了一種新的在頻選信道獲得滿分集滿增益的空時編碼方案.通過在不同的發送天線處設置隨機交織器，該空時碼滿足了行滿秩矩陣，從而能夠獲得滿分集.由于存在交織器的隔離，接收機可在相加關系、卷積關系以及相等關系之間進行迭代，從而使得接收機復雜度大幅度降低.仿真結果顯示，頻選衰落信道中，空時交織碼的誤碼率曲線非常接近理想分集曲線.因此該方案為多天線系統空時碼字設計提供了一個在復雜度和誤碼率性能方面表現都非常優秀的選擇.

References)

［1］李道本.信號的統計檢測與估計理論［M］.北京:科學出版社，2004:422－454 Li Daoben.Theory of signal detection and estimation［M］.Beijing:Science Press，2004:422 －454

［2］ Alamouti SM.A simple transmit diversity technique for wireless communications［J］.IEEE JSelect Areas Commun，1998，16(1):1451－1458

［3］ Tarokh V，Seshadri N，Calderbank A R.Space-time codes for high data rate wireless communications:performance criterion and code construction［J］.IEEE Trans Inform Theory，1998，44(2):744－765

［4］ Tarokh V，Jafarkhani H，Calderbank A R.Space-time block codes from orthogonal designs［J］.IEEE Trans Inform Theory，1999，45(7):1456 －1466

［5］ Gore D，Sandhu S，Paulraj A.Delay diversity codes for frequency selective channels［J］.IEEE Proc ICC，2002，3(6):1949 －1953

［6］ Lindskog E，Paulraj A.A transmit diversity scheme for channels with intersymbol interferencee［J］.IEEE Proc ICC，2000，1(3):307－311

［7］ Gamal H El，Damen M O.Universal space-time coding［J］.IEEE Trans Inform Theory，2003，49(5):1097 －1119

［8］李道本.一種具有零相關窗的擴頻多址編碼方法:中國，CN1321374［P］.2001 －11 －07 Li Daoben.A method of code division multiple access with zero correlation window:China，CN1321374［P］.2001 －11 －07

［9］王雪松，方莉，楊星，等.頻率選擇性衰落信道中的發射分集設計［J］.北京郵電大學學報，2010，33(6):78 －82 Wang Xuesong，Fang Li，Yang Xing，et al.Design of transmit diversity schemes in frequency selective channels［J］.Journal of Beijing University of Posts and Telecommunications，2010，33(6):78－82