邏輯推理不得循環論證

王偉民

(太和縣宮集鎮中心學校 安徽 阜陽 236652)

數學知識在物理解題中的應用屢見不鮮,而物理規律在數學推理中的運用真的是少之又少.文獻[1]以例舉的方式闡述了物理原理在數學推理中的應用,讀后讓人耳目一新.但仔細推敲又覺欠妥，因文中的一些邏輯推理犯了循環論證的錯誤.

先講一段題外話.恢復高考制度后的1979年,高考數學卷有這樣一道題目:敘述并證明勾股定理.有相當多的考生是利用余弦定理來進行論證的,過程非常的簡潔.

證明：△ABC中,由余弦定理得

c2=a2+b2-2abcosC

當∠C=90°時，cosC=0, 所以c2=a2+b2.

該推理過程看似滴水不漏，無懈可擊，應該得滿分，而實際結果卻得了零分.原因就是這些考生對勾股定理和余弦定理在數學史上出現的先后順序沒弄清楚，余弦定理的證明是建立在勾股定理的基礎上.換句話說,在勾股定理發現之前,是不可能有余弦定理的.所以,拿余弦定理作為條件論證勾股定理,在邏輯推理中,犯了循環論證的錯誤.

之所以講這段題外話，是因為文獻[1]中例1的推理，就出現與上述推理類似的問題.現分析如下.

【例1】利用重心和力矩原理證明

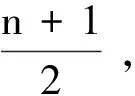
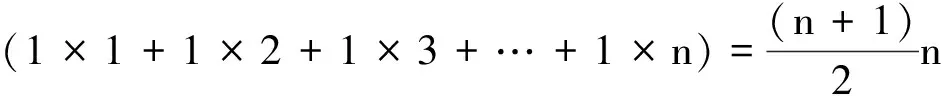
即

上面這段推理的問題出在“這n個質點組成系統的重心位置在這些點的正中間”上(原文中的語句為“它們的重心就是點1和點n的中點”).

建立與原分析中類似的物理模型,設這n個質點組成的系統重心橫坐標為x,由質心定義可得

(1×1+1×2+1×3+…+1×n) =xn

則

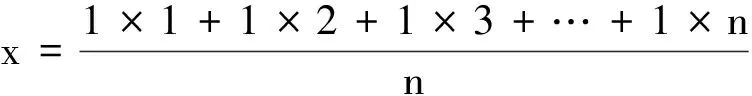
(1)

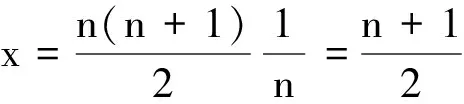
(2)

所以，這n個質點組成系統的重心在這些點的正中間位置.

用上述結論，還可進一步推出“質量分布均勻的硬棒，重心在其中點”的結論.

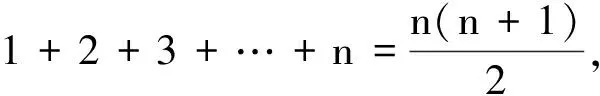
參考文獻

1 戎年中.利用物理學原理求解數學問題.物理通報，2009(10):16～18