幾種冷門圖像在物理解題中的妙用
王坦 王金聚
(浙江省溫州中學 浙江 溫州 325000)
物理圖像具有直觀、形象、簡明的特點,能直觀地描述物理過程,形象地表達物理規律,簡潔地闡明各物理量之間的相互關系,是分析、研究問題常用的方法之一.如運動學中的v-t,x-t圖像,電學中的U-I,i-t,u-t圖像,磁學中的B-t,Ф-t圖像,熱學中的p-V,V-T,p-T圖像等,在解題中使用頻率較高.但也有一些圖像雖不太常用, 有時用起來卻往往能“手到病除”、立竿見影,起到計算法所不能及的效果,現舉例如下.
1 ︱v︱-t圖像
對追及、相遇問題,有時涉及多個物體、多次相遇,物理過程多,情境復雜,難以建構清晰的運動圖景.此時,恰當地利用圖像,能直觀地展示復雜的物理情境,建構清晰的運動過程,拓展思維的深度與廣度,幫助我們找到解題的切入點.
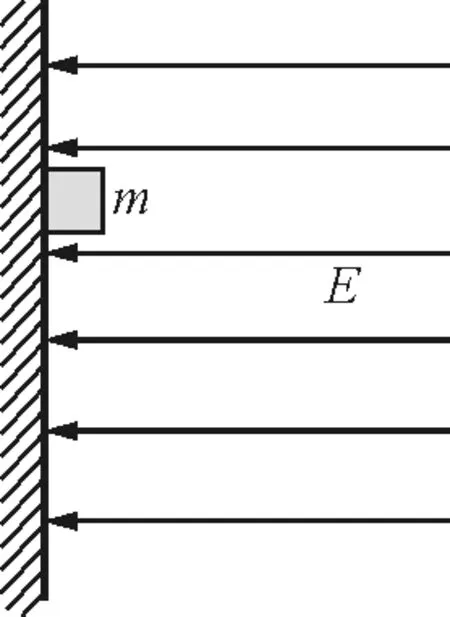
【例1】每顆子彈從槍口射出的速度大小都是30 m/s,某人每隔1 s豎直向上開一槍,假定子彈在升降過程中都不相碰,不計空氣阻力,試求:
(1)空中最多能有幾顆子彈.
(2)設t=0時將第1顆子彈射出,什么時刻與后面的子彈在空中相遇.
(3)每顆子彈分別能與幾顆子彈在空中相遇.
解析:以v表示速率,設子彈射出后經時間t到達最高點,由v0=gt,可得t=3 s.作出子彈在空中運動的速率-時間圖像,如圖1所示.圖中圖線①、②、③……分別表示第1顆子彈、第2顆子彈、第3顆子彈……的速率-時間圖像.顯然,任意兩條圖像的交點都表示兩子彈速率相同且一升一降時的情況,交點的橫坐標表示相遇的時刻,交點的縱坐標表示相遇時的速率大小.
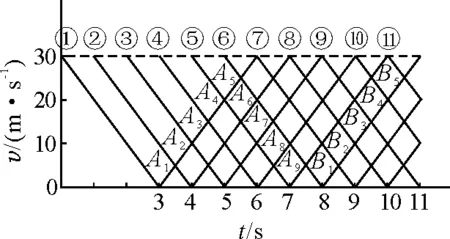
圖1
由圖1可知,當第7顆子彈即將射出時,第1顆子彈即將落地,所以說空中最多有6顆子彈.由于升、降圖線的斜率大小都表示重力加速度g,所以升、降圖線具有左右對稱性,由圖像可以直觀地看出第1顆子彈與其他子彈相遇時所對應的是圖中的A1,A2,A3,A4,A5點,相遇的時刻分別是t=3.5 s,4 s,4.5 s,5 s,5.5 s.
由于圖線的交點都對應相遇點,顯然,只要數一下每顆子彈的速率-時間圖線與其他子彈的圖線有幾個交點,就可以得出它與幾顆子彈在空中相遇.由圖1容易數出:第1顆相遇5顆,第2顆相遇6顆,第3顆相遇7顆,第4顆相遇8顆,第5顆會相遇9顆,從第6顆開始射出的子彈都相遇10顆.
第(2)、(3)問屬于多顆子彈的相遇問題.不難想象,若采用公式計算,比較復雜.若采用我們常使用的速度-時間圖像,則各子彈的圖線也不會相交,不能用交點形象地刻畫相遇點.但巧妙地選用速率-時間圖像,相遇點的情況在圖像中一目了然,相遇的時刻及速度大小都能在坐標系中直接讀出,方法巧妙,效果明顯.
2 Ep-h和Ek-h圖像
某些能量會隨距離呈線性變化,如重力勢能、電勢能等,都與距離有關.在涉及到有關能量隨距離變化的問題時,可以巧用圖像展示能量隨距離變化的動態過程,往往能從圖像上一目了然、直觀地得到結果,縮短了分析與推理的過程.
【例2】在地面上以初速度v0豎直上拋一個足球,空氣阻力不能忽略.足球在空中能上升的最大高度為hm,足球在上升過程距拋出點距離為h1處,足球的動能和重力勢能相等;下落過程中距拋出點距離為h2處,足球的動能和重力勢能相等,則下列說法中正確的是
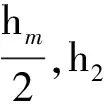
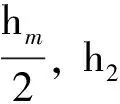
解析:本題涉及上升、下落兩個運動過程,兩過程中物體的動能、重力勢能均隨h變化而變化,屬動態變化問題,較為復雜. 以拋出點所在的平面作為重力勢能零勢能面,以h表示足球距拋出點的高度,在上升階段,根據動能定理可得
即Ek=Ek0-(mg+f)h
(1)
在下落階段,根據動能定理可得
即Ek=(mg-f)(hm-h)
(2)
重力勢能隨h變化的關系式為
Ep=mgh
(3)
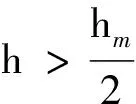
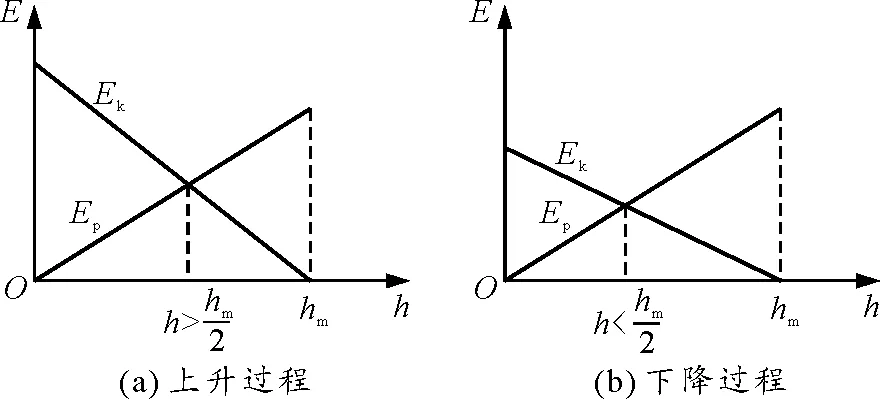
圖2
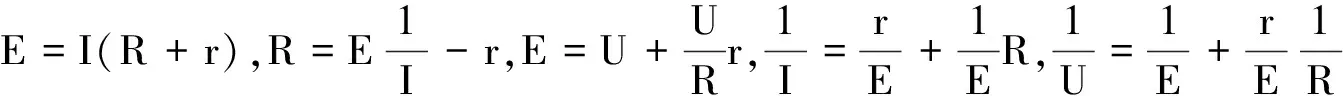
【例3】(2010年高考上海卷第29題)某同學利用DIS,定值電阻R0,電阻箱R1等實驗器材測量電池a的電動勢和內阻,實驗裝置如圖3.
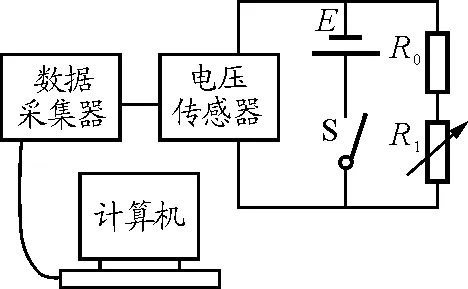
圖3
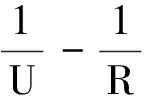
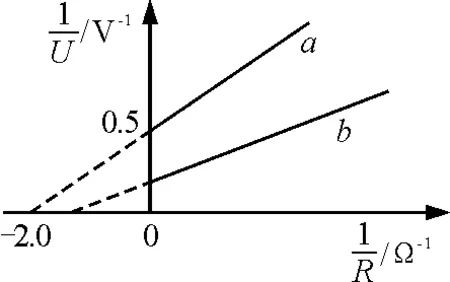
圖4
(1)由圖4中圖線a可知電池a的電動勢Ea=______V,內阻ra=______Ω.
(2)若用同一個電阻R先后與電池a及電池b連接,則兩電池的輸出功率Pa______Pb(填“大于”、“等于”或“小于”).兩電池的效率ηa______ηb(填“大于”、“等于”或“小于”).
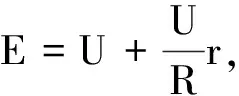
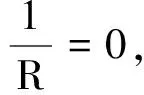
圖線a在縱軸上的截距為0.5 V-1,即
所以
Ea=2 V
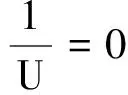
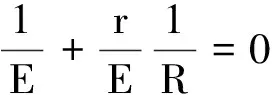
即
圖線a在橫軸上的截距為-2.0 Ω-1,所以
內阻
ra=0.5 Ω
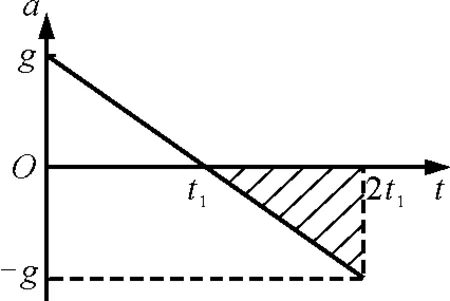
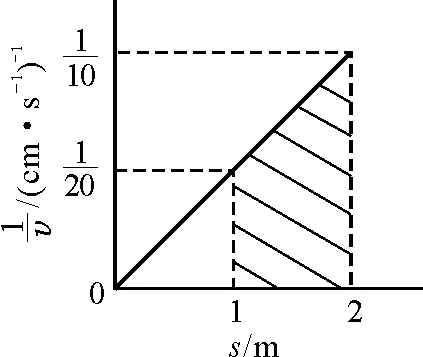
Ua Pa 電池的效率 所以 ra 代入上式得 ηa>ηb 有些物體的運動較為復雜,不是我們所熟悉的運動模型,無法用勻變速運動的規律求解,其v-t圖像也不呈直線.此時要解決問題,往往需要對兩坐標軸所代表的量進行靈活變動,目的是能把描述物體運動的圖像“化曲為直”,使直線的斜率與坐標軸所圍的面積等對應某些所求的物理量,用圖像法實現突破. 【例4】 一只老鼠從鼠洞沿直線爬出,已知爬出速度v的大小與距鼠洞中心的距離s成反比,當老鼠到達距鼠洞中心距離s1=1 m的A點時,速度大小為v1=20 cm/s.求當老鼠到達距鼠洞中心s2=2 m的B點時,其速度大小v2及老鼠從A點到達B點所用的時間t. 圖5 由圖5可得s=2 m時,老鼠的速度為10 cm/s.在1~2 m之間圖線與橫軸包圍的面積即為所求的時間,所以老鼠從A到B爬行的時間為 若物理量A,B,C滿足關系A=BC,則可以建立平面直角坐標系,以縱坐標表示B,橫坐標表示C,描繪出B,C的關系圖像,則圖線與橫坐標軸所圍的面積就可以表示物理量A. 【例5】 如圖6所示,一個質量為m,帶電荷量為+q的物體處于場強按E=kt規律(k為大于零的常數,取水平向左為正方向)變化的勻強電場中,物體與絕緣豎直墻壁間的動摩擦因數為μ,當t=0時,物體由靜止釋放.若最大靜摩擦力等于滑動摩擦力,且電場空間和墻面均足夠大,求: (1)物體經過多長時間運動速度達到最大; (2)最大速度是多少. 圖6 解析:(1)開始階段,分析物體的受力,可得 mg-μqkt=ma 隨著時間的延續,物體的加速度越來越小.當a=0時,物體的速度達到最大,此后做減速運動直至停止.所以在速度最大時有 mg-μqkt=0 即經過時間 物體在豎直墻壁上的速度達到最大值. (2)由mg-μqkt=ma,得 作出a-t圖像,如圖7所示.顯然,t軸之上三角形的面積大小代表速度的增加量,t軸之下三角形的面積大小表示速度的減少量.由于物體出發的初速度為零,所以最大速度就等于上面三角形的面積大小.即 圖7 該題利用圖像展示了復雜的動態過程,雖然不是我們所熟悉的勻變速運動,但可以根據圖線與坐標軸所圍面積的物理意義,簡捷明快地得出結果,令人耳目一新. 由此看來,圖像往往都蘊含著豐富的信息,如圖線的截距、斜率、拐點、圖線所圍面積、兩圖線交點等,都有各自的物理意義.巧借圖像解題,常常能化難為易、化繁為簡,特別是有些運用解析法無法解決的問題,常能從圖像上觸發靈感,另辟蹊徑,使問題迎刃而解,具有難以替代的作用.運用圖像解題也是高考重點考查能力之一.作為教師,應該在課堂教學中嘗試著滲透圖像法,把解析法與圖像法有機地結合起來,有意識地對學生進行圖像法解題的思維訓練,使學生熟練掌握這一重要的解題方法.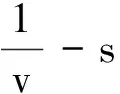
5 a-t圖像