例析微元法在變加速運動中的應用

吳正飛

(江蘇省如東高級中學 江蘇 南通 226400)

微元法是物理教學中的一種重要的思想方法，自2007年以來，微元法的考查在各地高考中年年出現，尤其是江蘇高考連續三年在壓軸題中涉及.我們發現微分的思想方法已被納入高中的教學范圍,例如，課本中就有兩個地方重點提出，一是分析勻變速直線運動的位移時，根據v-t圖像，把時間t內發生的位移進行微元分析，可以推導出勻變速直線運動的位移公式；二是分析勻速圓周運動的向心加速度時，根據加速度的定義，對圓周運動的速度的變化進行微元分析，可以推導向心加速度的表達式.因此，該方法在高考試題中頻繁出現就不足為奇了，但是每年學生在這類問題中的得分率都很低，原因在于學生沒有真正深刻領悟到微元法的精髓，以及它的使用方法和使用技巧.

微元法是一種利用微分思想的分析方法.具體而言就是將研究對象或物理過程進行無限細分(化變為恒、化曲為直、化整為零)，從其中抽取某一微小單元進行討論，從而找出被研究對象或被研究過程變化規律的一種思想方法. 該方法可以使一些復雜的物理過程用我們熟悉的物理規律迅速加以解決，使所求問題簡單化.

利用微元法解題一般分為三步.

第一步,選擇恰當的微元(如空間元、時間元)作為突破整體研究的對象.微元可以是一小段線段、圓弧、一小塊面積、一個小體積、小質量、一小段時間……但應具有整體對象的基本特征.第二步,將微元模型化(如視作點電荷、質點、勻速直線運動、勻速轉動……)并運用相關物理規律，求解這個微元.第三步,將一個微元的求解結果推廣到其他微元，并充分利用各微元間的關系(如對稱關系、矢量方向關系、量值關系等)，對各微元的解出結果進行疊加，以求出整體量的合理結果.下面就通過實例分析微元法在求解變加速運動中的各種物理量的使用方法.

1 利用微元法求解變加速運動中的速度

在電磁感應與力學結合的問題中，由于受安培力作用，導體棒的速度發生變化，而速度又會改變安培力，從而使得導體棒做變加速運動.此時，力學的常規方法很難解決，若考慮到微元法，再結合力學知識則可迎刃而解.

【例1】如圖1所示，間距為L的兩條足夠長的平行金屬導軌與水平面的夾角為θ，導軌光滑且電阻忽略不計．場強為B的條形勻強磁場方向與導軌平面垂直，磁場區域的寬度為d1，間距為d2．兩根質量均為m,有效電阻均為R的導體棒a和b放在導軌上，并與導軌垂直(設重力加速度為g)．

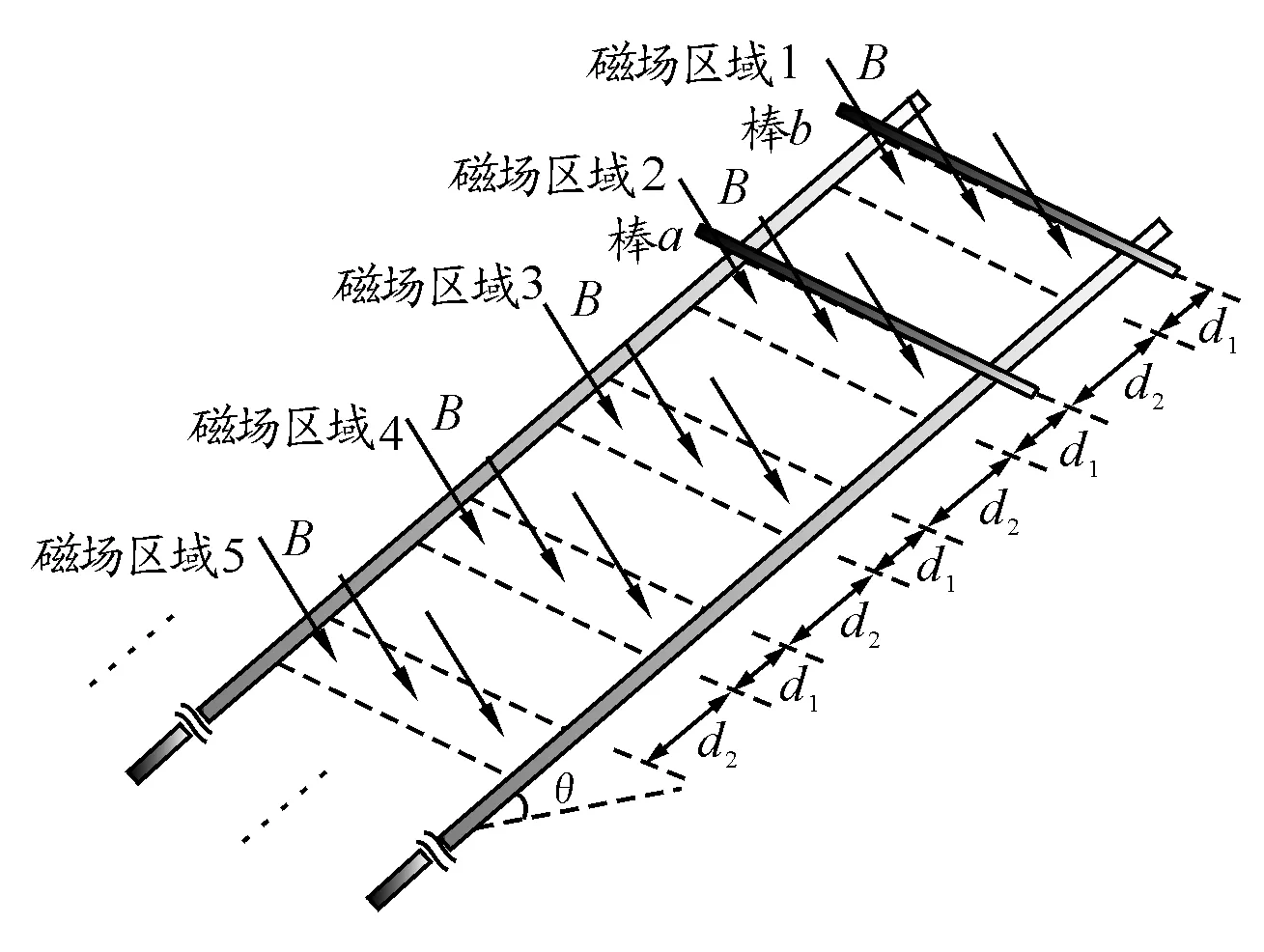
圖1

(1)若a進入第2個磁場區域時，b以與a同樣的速度進入第1個磁場區域，求b穿過第1個磁場區域過程中增加的動能ΔEk；

(2)若a進入第2個磁場區域時，b恰好離開第1個磁場區域；此后a離開第2個磁場區域時，b又恰好進入第2個磁場區域．且a,b在任意一個磁場區域或無磁場區域的運動時間均相等．求b穿過第2個磁場區域過程中，兩導體棒產生的總焦耳熱Q；

(3)對于第2問所述的運動情況，求a穿出第k個磁場區域時的速率v．

解析： (1)ΔEk=mgd1sinθ;

(2)Q=mg(d1+d2)sinθ;

(3)設導體棒在無磁場區域和有磁場區域的運動時間都為t，在無磁場區域有

v2-v1=gtsinθ

(1)

且平均速度

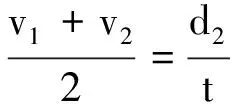
(2)

在有磁場區域，對a棒

F=mgsinθ-BIl

且

解得

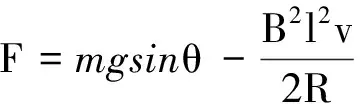
(3)

因為速度v是變量，用微元法根據牛頓第二定律, 在一段很短的時間Δt內

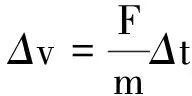
則有

因為導體棒剛進入磁場區時的速度為v2,剛離開磁場區時的速度為v1, 所以

∑Δv=v1-v2∑vΔt=d1∑Δt=t

因此

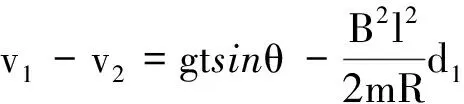
(4)

聯立式(1)～(3),得

a,b在任意一個磁場區域或無磁場區域的運動時間均相等, 所以，a穿出任一個磁場區域時的速率v就等于v1．因此

2 利用微元法求解變加速運動中的位移

在力學中，常遇到物體受變力作用的情形，因為牛頓定律和運動學公式無法使用，所以，大部分學生就束手無策.其實我們可以拓寬思維，在變化中找不變，即可以化整為零，此時可能就會豁然開朗，發現其中的特殊規律，從而找到解題的突破口.

【例2】從地面上以初速度v0豎直向上拋出質量為m的球，若運動過程中受到的空氣阻力與其速率成正比，球運動的速率隨時間變化規律如圖2所示，t1時刻到達最高點，再落回地面，落地時速率為v1，且落地前球已經做勻速運動.求：

(1)球從拋出到落地過程中克服空氣阻力所做的功;

(2)球拋出瞬間的加速度大小;

(3)球上升的最大高度.

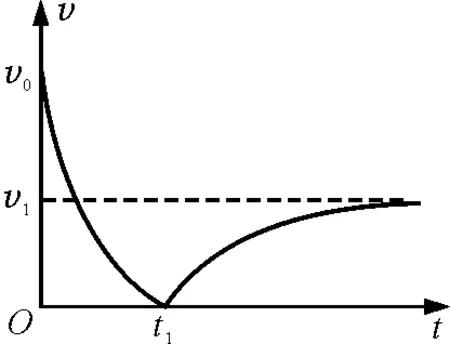
圖2

解析：

(3)設上升至速度為v時加速度為a，則

取極短時間Δt，其速度變化為Δv，有

又因為

vΔt=Δh

對上升全過程有

即

解得

3 利用微元法求解變加速運動中的電量和能量

在中學物理解題中，求解電荷量和能量往往是學生的弱點，尤其在力、電結合的綜合類問題中，再遇到變加速運動時就會難上加難.這時對學生的綜合分析的能力要求就很高，但是如果能掌握合理的解題方法則會簡單很多.微元法就是解決這類問題的理想方法.

【例3】如圖3所示，很長的光滑磁棒豎直固定在水平面上，在它的側面有均勻向外的輻射狀的磁場.磁棒外套有一個質量均勻的圓形線圈，質量為m，半徑為R，電阻為r，線圈所在磁場處的磁感應強度為B.讓線圈從磁棒上端由靜止釋放沿磁棒下落，經一段時間與水平面相碰并反彈，線圈反彈速度減小到零后又沿磁棒下落，這樣，線圈會不斷地與水平面相碰下去，直到停留在水平面上.已知第一次碰后反彈上升的時間為t1，下落的時間為t2，重力加速度為g，不計碰撞過程中能量損失和線圈中電流磁場的影響.求：

(1)線圈第一次下落過程中的最大速度vm;

(2)第一次與水平面碰后上升到最高點的過程中通過線圈某一截面的電荷量q;

(3)線圈從第一次到第二次與水平面相碰的過程中產生的焦耳熱Q.

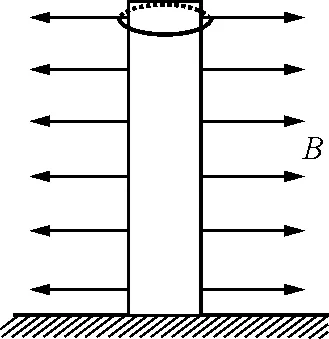
圖3

解析：

(2)反彈后上升的過程中某一時刻，由牛頓運動定律得

mg+BI2πR=ma

在一段微小時間Δt內，速度增量為Δv=aΔt，通過線圈截面電荷量為Δq=IΔt,則

(3)反彈后上升的過程中某一時刻，由牛頓運動定律得

在一段微小時間Δt內，速度增量為Δv=aΔt，線圈上升高度為Δh=vΔt，則線圈可上升的最大高度h為

線圈到達最高點后，下落過程中的某一時刻，由牛頓運動定律得

在一段微小時間Δt內，速度增量為Δv=aΔt，線圈下降高度為Δh=vΔt，則線圈第二次下降到水平面時的速度為v

此過程的線圈中產生的熱量為線圈動能的損失

化簡得

從上述實例可以發現，在處理變加速運動問題時，常常遇到運動過程中求解時間、速度、位移、電荷量、能量等問題，用常規方法很難解決，但靈活運用微元的思想，這些問題都可以迎刃而解.因此，微元法為高中物理的學習提供了更好的數學工具，使得高中物理不僅可以從研究方法上得到提升，也使得學生利用數學方法處理物理問題的能力得到提高.所以，教師在物理教學中，應逐步滲透微元思想并加強訓練.實踐證明，經過悉心培養，大部分學生都能夠做到微元法思想的創新與拓展轉移.只有師生共同努力才能將微元法真正應用到物理學中.