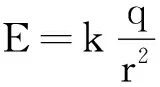淺談高考“物理分析”試題的解答方法

干 恒

(犍為第一中學 四川 樂山 614400)

近年來北京、福建等地的高考物理試題中出現了一類“物理分析”特色試題，這類試題的特點是高中生無法或難以直接解答，只有根據所學的物理知識，通過一定的分析、判斷來確定問題解的合理性或正確性.對于這類問題往往要進行合理地近似處理，讓其回歸到高中物理的常規模型中方能有效地解答.

1 對一道“黑榜”物理分析試題的平反

【例1】(2011年高考福

圖1

建理綜卷第18題)如圖1，一不可伸長的輕質細繩跨過滑輪后，兩端分別懸掛質量為m1和m2的物體A和B.設滑輪與繩質量為m且分布均勻，滑輪轉動時與繩之間無相對滑動，不計滑輪與軸之間的摩擦.設細繩對A和B的拉力大小分別為T1和T2，已知下列4個關于T1的表達式中有一個是正確的，請你根據所學的物理知識，通過一定的分析，判斷正確的表達式是

文獻[1]把這個題列入“黑榜”，文中寫道：“高中學生要解答這道試題，只能采用特殊值代入法，把A，B的質量設置為特定值，代入上述4個選項的公式，從計算結果來判斷，看哪些選項的答案是不合理的；把所有不合理的選項排除掉，如果還剩下一個選項，所剩選項就是答案.”同時，該文獻認為這種只用“排除法”的考法不應該是一種值得弘揚的考查方式.筆者認為只要進行合理近似(極限)處理，這個題就可以回歸到高中的常規模型——牛頓運動定律能解決的“聯接體”問題.

1.1 嚴格的解法

設m1>m2，滑輪的半徑為R,物體A，B的加速度大小為a,滑輪的轉動慣量為I,角加速度為β，對A，B，由牛頓第二定律得

m1g-T1=m1a

(1)

T2-m2g=m2a

(2)

對滑輪由轉動定律得

T1R-T2R=Iβ

(3)

(4)

(5)

聯立式(1)～(5)解得

故正確答案為選項C.

1.2 合理近似處理回歸高中常規模型的解法

當設滑輪的質量m?m1，m?m2，可忽略，即可認為m=0，就可以轉化為高中的“聯接體”問題，解法如下.

設m1>m2，A,B的加速度大小為a,由于m=0,故T1=T2=T.對A,B,由牛頓第二定律得

m1g-T=m1a

(6)

T-m2g=m2a

(7)

由式(6)、(7)解得

將m=0帶入選項中，只有選項C與上式相同，所以選項C正確.

可見，此題不只是用“排除法”才能解答.該題很好地考查了學生的理解能力、推理能力、分析綜合能力以及知識遷移能力，是一個具有引導高中物理教育與大學物理教育銜接作用，有一定價值的好題.

2 對兩道高考“物理分析”試題的解答

【例2】(2008年高考北京理綜卷第20題)有一些問題你可能不會求解，但是你仍有可能對這些問題的解是否合理進行分析和判斷.例如，從解的物理量單位，解隨某些已知量變化的趨勢，解在一些特殊條件下的結果等方面進行分析，并與預期結果、實驗結論等進行比較，從而判斷解的合理性或正確性.

圖2

對于上述解，某同學首先分析了等號右側量的單位，沒發現問題，就進一步利用特殊條件對該解做了如下4項分析和判斷，所得結論都是“解可能是對的”.但是，其中有一項是錯誤的.請你指出該項

A.當θ=0°時，該解給出a=0，這符合常識，說明該解可能是對的

B.當θ=90°時，該解給出a=g，這符合實驗結論，說明該解可能是對的

C.當M?m時，該解給出a=gsinθ，這符合預期的結果，說明該解可能是對的

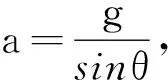
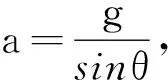
【例3】(2010年高考福建理綜卷第18題)物理學中有些問題的結論不一定必須通過計算才能驗證，有時只需要通過一定的分析就可以判斷結論是否正確.圖3為兩個彼此平行且共軸的半徑分別為R1和R2的圓環，兩圓環上的電荷量均為q(q>0)，而且電荷均勻分布.兩圓環的圓心O1和O2相距為2a，聯線的中點為O，軸線上的A點在O點右側與O點相距為r(r

圖3

由R1?a+r,R2?a-r條件進行近似處理得選項B中

選項D中

故正確答案為選項D.

物理問題多數都是在近似(抓主要因素，忽略次要因素)情況下解決的，因此，把物理條件進行合理的近似(極限)處理，把不能解決的復雜物理問題轉化為熟悉的常規模型，用已有知識能解決的問題應該成為學生的物理能力的重要組成部分.

參考文獻

1 黃恕伯.2011年高考物理試題“紅黑榜”.基礎教育課程，2011(9)：39～43