轉動慣量與慣性質量的轉換關系

張軍平

(復旦大學計算機科學技術學院 上海 200433)

1 簡介

剛體的定軸轉動中，當轉動慣性系與平動參考系并存時，其問題的求解需要涉及多個經典力學的物理概念，如動量守恒、角動量守恒、力矩公式、能量守恒等等.尤其在考慮與滑輪相關的問題時，學生更容易混淆相關物理概念.

在教學中，筆者發現可以將與滑輪組相關的剛體定軸轉動問題，轉化到平動慣性系來快速求解.其中關鍵的技巧是將轉動慣性系中的轉動慣量轉換成平動慣性系中的慣性質量.在解題時，這一技巧能較方便地解決相關的問題并促進學生對剛體定軸轉動的理解.

本文在余下的部分首先簡要回顧轉動慣量的基本知識，提出轉動慣量與平動慣性系的慣性質量的轉換關系，并給出了一組推論.然后，通過3個實例驗證了這一處理的有效性.最后,對文章進行了總結.

2 轉動慣量與慣性質量的轉換

轉動慣量是剛體轉動時具有的一種“慣性”.與平動慣性系下的慣性質量相似，均表現為阻礙物體的運動.不同在于，慣性質量是阻礙物體或質點的平動，而轉動慣量是阻礙質點、質點系和剛體的轉動；其次，平動慣性系的慣性質量與參考系的選擇(在低速意義下)無關，而轉動慣量則與剛體的形狀和參考原點的選擇密切相關[1～4].

因此，在處理與剛體定軸轉動相關的題型時，首先要考慮的是轉動慣量的計算，然后進行受力分析，其中如何有效引入轉動慣量需要仔細考慮.例如，在與滑輪轉動、含平動的轉動等相關的題型中，利用下面兩個公式的等價性往往是最常見的一步

M=r×F

(1)

M=Jα

(2)

式中r表示受力點與定軸參考原點之間的距離矢量，F表示受力點上的外力矢量，J是剛體的轉動慣量，α是剛體的角加速度，M是力矩.利用式(1)、(2)的等價性，可以對與滑輪相關的題型進行有效分析，并很好地引入轉動慣量的概念.而如果題型涉及能量守恒時，則需要引入轉動動能，即

(3)

這里Ek表示轉動動能，ω表示角速度.

在教學中，筆者發現當從以上角度求解與滑輪組相關的題型時，學生往往很難較快地發現題型中隱含的各種條件.一個可能的原因是滑輪組相關的題型里實質上體現了經典力學中多個概念性的組合，同時需要從兩種不同參考系(平動慣性系與轉動參考系)來分析問題.因此，如果能將兩個參考系通過轉換成單個參考系(如平動慣性系)來分析，則問題的難度有可能會下降.

基于以上觀察，發現對于半徑為R，元質量均勻分布，總質量為m，以圓的中心為定軸轉動的滑輪而言，其轉動慣量J可以由下式進行轉換，看成是平動慣性系中的“偽”慣性質量mpseudo為

(4)

其直觀理解為當存在滑輪的轉動時，其在平動慣性系的“偽”慣性質量等價于轉動參考系的轉動慣量除以受力點到剛體定軸轉動原點的距離的平方.

為方便閱讀，式(4)的理論性分析可參考本文的附錄部分.

基于式(4)，不難得出4種不同剛體定軸轉動時，其相對應的“偽”慣性質量的大小，如表1.

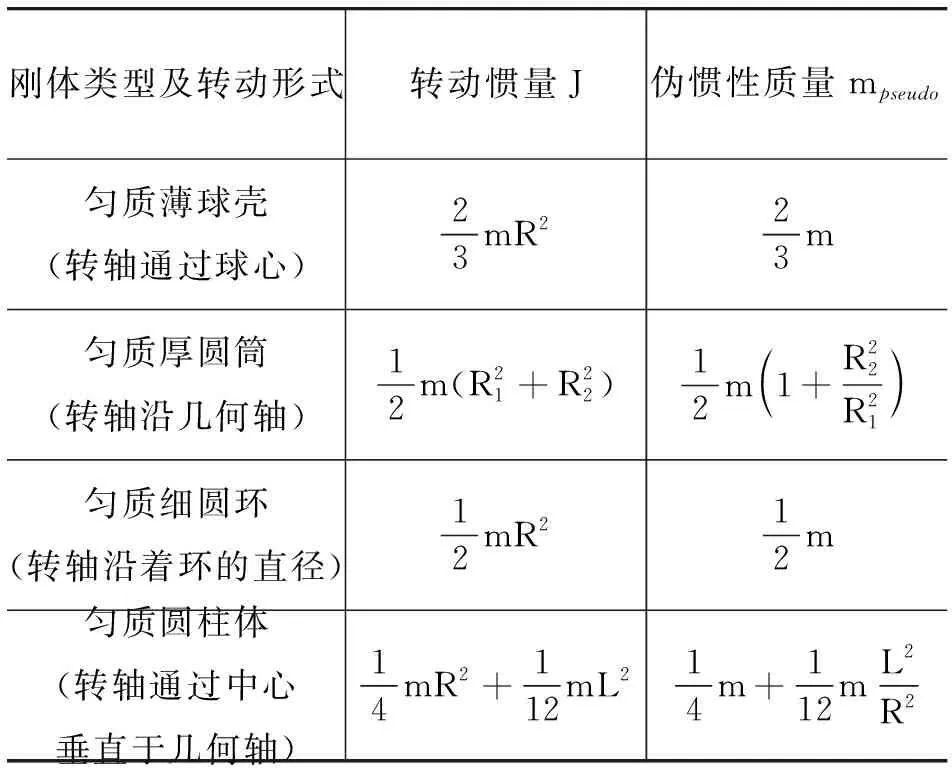
表1 剛體轉動慣量與“偽”慣性質量的對應

表中m表示剛體的總質量，R，R1為剛體定軸旋轉時距旋轉剛體的原點的半徑，R2為勻質厚圓筒的內壁半徑，L是勻質圓柱體的長度.勻質矩形薄板的“偽”慣性質量大小依賴于定軸旋轉的方向.

3 示例分析

在本節中，我們期望對以下3種剛體力學的題型，按文中提出的轉換技巧重新進行受力分析和求解.

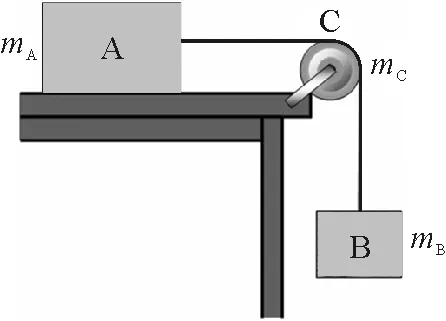
圖1 含平動的轉動問題示例1

【例1】質量為mA的物體A靜止在光滑水平面上，和一質量不計的繩索相連接，繩索跨過一半徑為R，質量為mC的圓柱形滑輪C，并系在另一質量為mB的物體B上，滑輪與繩索間沒有滑動，且滑輪與軸承間的摩擦力可略去不計，如圖1所示，問：

(1)兩物體的線加速度為多少？水平和垂直兩段繩索的張力各為多少？

(2)若滑輪與軸承間的摩擦力不能忽略，并設它們間的摩擦力矩為Mf，求線加速度及繩的張力.

分析：這一題型的特點是轉動剛體和平動剛體并存.這就要求學生能較好地運用隔離法對物體進行受力分析，同時能熟練地運用牛頓第二定律、轉動定律來列方程和求解，因此是一道綜合題，目的是考查學生對經典力學的理解和貫通，具有一定的難度.

(1)如果將這種轉動剛體和平動剛體并存的情況，轉化為僅考慮平動慣性系的力學問題，則可以得到簡化的求解過程.依式(4)，首先將具有轉動慣量J的滑輪進行轉換，變換成平動慣性系的“偽”慣性質量mpseudo，這一質量等于

(5)

則可重新分析圖1 的受力情況.因為如果將3個物體視為一個系統時，則所受的合外力應為

F=mg

(6)

其中g為重力加速度.同時，這一合外力對平動慣性系有一個整體的加速度，即滿足

F=mta

(7)

這里在平動慣性系意義下系統的總質量mt滿足

mt=mA+mB+mpseudo=

(8)

聯立式(6)、(7)，可得線加速度為

(9)

利用基本的受力分解，可以得到水平和垂直兩段繩索的張力.這里就不再贅述.

(2)如果存在摩擦力矩，考慮到合外力矩M具有式(1)的形式, 可以得到摩擦力矩的力Ff為

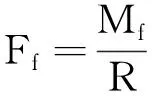
(10)

因為力Ff是阻礙物體運動的力，在本系統中表現為與物體B的運動方向相反，所以,將產生摩擦力矩的力Ff代入式(6)右端，則有

(11)

聯立式(7)、(8)、(11)，可得存在摩擦力矩時系統的線加速度為

(12)

相應地，我們可以基于式(12)自然推導此時水平和垂直兩段繩索的張力.

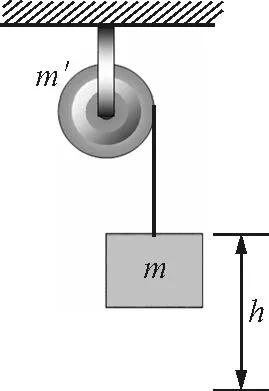
圖2 含平動的轉動問題示例2

【例2】一質量為m′,半徑為R的圓盤，可繞一垂直通過盤心的無摩擦的水平軸轉動.圓盤上繞有輕繩，一端掛質量為m的物體.如圖2所示.問物體由靜止下落高度h時，其速度的大小為多少？設繩的質量忽略不計.

分析：這一題型的特點也是轉動剛體和平動剛體并存.教授這一題型的目的是要讓學生理解在合外力及非保守內力為零的前提下系統內部的機械能守恒.由于包含剛體的轉動和平動，解題的關鍵在于要清楚地知道動能可分為平動動能和轉動動能兩部分.

如果我們同樣將這一轉動與平動相混合的問題，通過式(4)將轉動部分的轉動慣量變換為平動部分的“偽”慣性質量，則本題中平動慣性系意義下系統的總質量mt顯然滿足

(13)

通過受力分析，易知系統僅受作用于質量為m的物體上的重力作用，同時，此重力作用在系統上會產生一個加速度，故有

(14)

由此可知，系統的加速度a為

(15)

考慮到速度與加速度及高度的關系和初始條件，可得

(16)

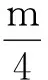
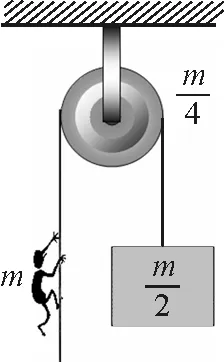
圖3 含平動的轉動問題示例3

分析：原題主要考查學生對角動量定理的應用，同時，需注意的是題中既包含質點的角動量，也有剛體的角動量.由于具有兩個質點和一個剛體，學生在受力分析和計算過程中都容易產生概念的混淆.標準的求解方法參見文獻[5].

依據筆者提出的轉換關系，則可以首先按式(4)將滑輪組具有的轉動慣量變為“偽”慣性質量，即

(17)

因此，在轉換意義下，系統的總質量mt為

(18)

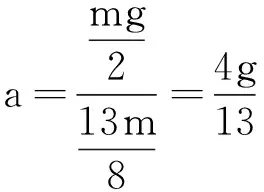
(19)

從以上解法不難發現，首先，通過提出的轉換技巧來求解以上含平動的轉動問題時，可以使問題求解簡化，且只要考慮如何將轉動慣量通過式(4)轉換成“偽”慣性質量，隨后的過程僅涉及牛頓第二定律的基本概念.其次，通過提出轉換技巧，建立了轉動慣性系與平動慣性系之間的聯系.另外，引用的定理和最終求解思路沒有影響學生對物理概念的理解.最后，在課堂上同時教授原解題策略和筆者提出的轉換關系，可以使學生加深對經典力學知識的了解，并可以讓學生了解到這一問題求解的多樣性.

4 結論

文章通過研究轉動慣量與慣性質量的轉換關系，將轉動慣量變換為平動慣性系的“偽”慣性質量.當處理一類具有平動、轉動混合的，與剛體相關的力學題型時，這一轉換可以簡化原有的解題思路，使得具有兩個不同參考系的問題可以在同一框架下求解，在教學時可以幫助啟發和活躍學生的思維，并能使學生更好地理解經典力學的基本概念和知識.

參考文獻

1 張三慧.大學物理第一冊(第二版).北京：清華大學出版社，1999

2 程守洙，江之永.普通物理學第一冊(第五版) .北京：高等教育出版社,1998

3 梁勵芬，蔣平.大學物理簡明教程.上海：復旦大學出版社, 2002

4 (美)費恩曼，萊頓，桑茲著.鄭永令，華宏鳴，吳子儀,等譯.費恩曼物理學講義(第一卷).上海：上海科學技術出版社，2005

5 胡盤新.大學物理解題方法與技巧.上海:上海交通大學出版社，2004.126～127

附錄：

A.轉動慣量與“偽”慣性質量的轉換關系的理解

附錄A旨在給出式(4)的基本理解.由于剛體定軸轉動時受到外力作用，其合力矩公式總可以有下面的關系

RFT2-RFT1=Jα

(A-1)

其中R是剛體定軸轉動時距定軸點的距離，α是角加速度，J是轉動慣量.FT1，FT2為剛體轉動部分所承受的外力.

而又知

所以，式(A-1)可轉換為

(A-2)

我們又知道，牛頓第一定律指出，在平動慣性系中，力是改變物體運動狀態的原因.同時，牛頓第二定律表明力作用在質點上時，可以產生直線加速度，其公式一般寫為

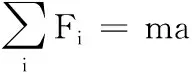
(A-3)

由此可以推斷，在多數與剛體定軸相關的習題中，可以通過式(4)來估計物體在平動慣性系下的“偽”慣性質量，從而簡化原有問題的求解.