把握追問(wèn)時(shí)機(jī) 促進(jìn)有效思維
2011-12-29 00:00:00商純潔
小學(xué)教學(xué)研究 2011年7期
在小學(xué)數(shù)學(xué)教學(xué)中,提問(wèn)是引發(fā)師生對(duì)話的重要手段。數(shù)學(xué)學(xué)科具有高度的抽象性,而小學(xué)生卻是以形象思維為主。因此,對(duì)于一個(gè)數(shù)學(xué)知識(shí)點(diǎn),僅有一問(wèn)是不夠的,教學(xué)中教師要根據(jù)課堂實(shí)際情況適時(shí)進(jìn)行二度追問(wèn),這樣才能引導(dǎo)學(xué)生對(duì)知識(shí)點(diǎn)進(jìn)行深入思考,從而有效提高思維品質(zhì)。
一、在認(rèn)知錯(cuò)誤時(shí)追問(wèn)——糾正思維偏差
小學(xué)生的年齡還小,他們的抽象思維水平還不是很高。在數(shù)學(xué)學(xué)習(xí)的過(guò)程中,他們經(jīng)常會(huì)因?yàn)槭艿街R(shí)負(fù)遷移的作用而產(chǎn)生錯(cuò)誤。課堂是允許學(xué)生犯錯(cuò)的地方,學(xué)生的錯(cuò)誤也往往是他們真實(shí)的學(xué)習(xí)起點(diǎn)。因此,當(dāng)學(xué)生的數(shù)學(xué)學(xué)習(xí)出現(xiàn)錯(cuò)誤時(shí),教師要適時(shí)通過(guò)追問(wèn)引導(dǎo)學(xué)生自己去發(fā)現(xiàn)錯(cuò)誤,呈現(xiàn)出錯(cuò)誤思維的運(yùn)行軌跡,從而糾正思維偏差。
[案例]《能被3整除的數(shù)的特征》教學(xué)片段
師:同學(xué)們,上一節(jié)課我們已經(jīng)學(xué)習(xí)了《能被2和5整除的數(shù)的特征》。那么,什么樣的數(shù)能被2整除呢?
生1:個(gè)位是2、4、6、8、0的數(shù)就能夠被2整除。
生2:一個(gè)數(shù)如果個(gè)位上的數(shù)能夠被2整除,那么這個(gè)數(shù)就能夠被2整除。
師:那么什么樣的數(shù)能夠5整除呢?
生3:個(gè)位是5和0的數(shù)能夠被5整除。
生4:一個(gè)數(shù)如果個(gè)位上的數(shù)能夠被5整除,那么這個(gè)數(shù)就能夠被5整除。
師:這一節(jié)課我們要學(xué)習(xí)《能被3整除的數(shù)的特征》。同學(xué)們,你們覺(jué)得怎樣的數(shù)能夠被3整除?
生5:個(gè)位是3、6、9、0的數(shù)就能夠被3整除。
師:你為什么這樣想呢?
生5:前面我們?cè)趯W(xué)習(xí)《能被2和5整除的數(shù)的特征》時(shí)知道,一個(gè)數(shù)如果個(gè)位上的數(shù)能夠被2和5整除,那么這個(gè)數(shù)就能夠被2和5整除。我想,如果一個(gè)數(shù)的個(gè)位是3、6、9、0,也應(yīng)該是能夠被3整除的。
師:同學(xué)們,你們也是這樣想的嗎?
大部分同學(xué)都表示贊同這一種觀點(diǎn),于是教師這樣進(jìn)行追問(wèn):那么一個(gè)數(shù)的個(gè)位是3、6、9、0,是不是就一定能夠被3整除呢?你們有沒(méi)有辦法來(lái)證明?
生:我們只要寫一些數(shù),然后試一試就行了。(同學(xué)們紛紛開始寫起數(shù)來(lái)進(jìn)行驗(yàn)證。過(guò)了一會(huì)兒有的同學(xué)開始發(fā)現(xiàn)不對(duì)了)
生1:我剛才寫了13、16和19這三個(gè)數(shù)。但這三個(gè)數(shù)都是不能被3整除的。
生2:是呀,我寫的數(shù)是20和26,也不能被3整除。
生3:我寫的數(shù)是29、33和36。其中29是不能被3整除的。
生4:看來(lái),剛才我們的猜想是錯(cuò)誤的。一個(gè)數(shù)的個(gè)位是3、6、9、0,這個(gè)數(shù)不一定能被3整除。
以上教學(xué)片段中,學(xué)生產(chǎn)生“一個(gè)數(shù)的個(gè)位是3、6、9、0,就能被3整除”這個(gè)錯(cuò)誤是因?yàn)槭艿搅恕澳鼙?和5整除的數(shù)的特征”知識(shí)負(fù)遷移的影響。當(dāng)學(xué)生出現(xiàn)錯(cuò)誤時(shí),教師適時(shí)追問(wèn)“一個(gè)數(shù)的個(gè)位是3、6、9、0,是不是就一定能夠被3整除呢?你們有沒(méi)有辦法來(lái)證明?”學(xué)生開始了證明之旅,他們?cè)诶e證明的過(guò)程中發(fā)現(xiàn)原來(lái)的猜想是錯(cuò)誤的,從而糾正了思維偏差。
二、在表達(dá)膚淺時(shí)追問(wèn)——暴露思維方法
“語(yǔ)言是思維的外殼。”小學(xué)生的語(yǔ)言表達(dá)能力不是很強(qiáng),在數(shù)學(xué)學(xué)習(xí)中他們往往不能深刻地表達(dá)自己的思維過(guò)程,課堂上對(duì)于一些數(shù)學(xué)現(xiàn)象的表述他們往往顯得比較淺顯。此時(shí),教師要提供給學(xué)生充分思考和表達(dá)的時(shí)間,通過(guò)追問(wèn)的方式給他們搭建思維的跳板,暴露思維方法,從而突破表面現(xiàn)象,在更高層次上繼續(xù)進(jìn)行思考。
[案例]《平均分》教學(xué)片段
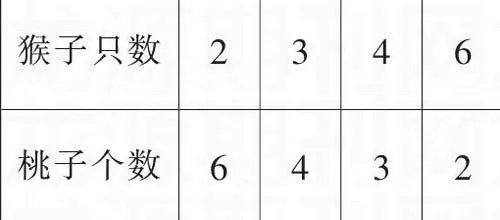
在教學(xué)《平均分》一課時(shí),練習(xí)環(huán)節(jié)教師給學(xué)生設(shè)計(jì)了這樣一道開放題:有12個(gè)桃子可以平均分給幾只猴子,每只猴子分到幾個(gè)桃子?
生1:可以分給2只猴子,每只猴子分到6個(gè)桃子。
生2:可以分給3只猴子,每只猴子分到4個(gè)桃子。
生3:可以分給4只猴子,每只猴子分到3個(gè)桃子。
生4:可以分給6只猴子,每只猴子分到2個(gè)桃子。
學(xué)生回答后,我出示以下表格:
師:同學(xué)們,請(qǐng)你們仔細(xì)觀察這一張表格,你有什么發(fā)現(xiàn)?
生:我發(fā)現(xiàn)從左往右看上一行的數(shù)是2、3、4、6,下一行的數(shù)是6、4、3、2。
生1:這兩行數(shù)上一行和下一行剛好反一下。
學(xué)生的回答顯然是淺顯的,于是教師這樣進(jìn)行追問(wèn):小朋友們,你們剛才是怎么進(jìn)行觀察的?
生1:剛才我先觀察了上面一行的數(shù),再觀察下面一行的數(shù)。
生2:在表格中,上一行數(shù)2、3、4、6,是從小到大的規(guī)律,下一行數(shù)6、4、3、2是從大到小的規(guī)律。
教師繼續(xù)追問(wèn):上一行數(shù)表示什么?下一行數(shù)又表示什么呢?
生3:上一行數(shù)表示猴子的只數(shù),下一行數(shù)表示每只猴子分到的桃子的個(gè)數(shù)。
生4:我明白了,12個(gè)桃子是不變的,上一行猴子的只數(shù)分別是2、3、4、6,猴子的只數(shù)越來(lái)越多,所以每只猴子分到的桃子的個(gè)數(shù)應(yīng)該是越來(lái)越少,所以下一行數(shù)是從大到小了,分別是6、4、3、2。
生5:是啊。下一行數(shù)是隨著上一行數(shù)的變化而變化的。上一行數(shù)越大,也就是說(shuō)猴子的只數(shù)越多,下一行就越小,每只猴子分到的桃子的個(gè)數(shù)就少了。
……
以上案例中,當(dāng)學(xué)生的語(yǔ)言表達(dá)比較淺顯時(shí),教師適時(shí)進(jìn)行了兩次追問(wèn)“你們剛才是怎么進(jìn)行觀察的”“ 上一行數(shù)表示什么,下一行數(shù)又表示什么呢”,有效引導(dǎo)學(xué)生暴露了思維的過(guò)程。在追問(wèn)的引導(dǎo)下,學(xué)生把原來(lái)上下兩行孤立的數(shù)據(jù)聯(lián)系了起來(lái),思維逐步走向深入,發(fā)現(xiàn)猴子的只數(shù)和每只猴子分到的桃子的個(gè)數(shù)之間存在的規(guī)律——在桃子總數(shù)一定的情況下,猴子的只數(shù)越多,每一只猴子分到的桃子的個(gè)數(shù)就越少。
三、在意外生成時(shí)追問(wèn)——推進(jìn)思維進(jìn)程
新課程理念特別強(qiáng)調(diào)課堂教學(xué)中的生成。在小學(xué)數(shù)學(xué)課堂上,小學(xué)生的數(shù)學(xué)學(xué)習(xí)經(jīng)常會(huì)出現(xiàn)教師預(yù)設(shè)之外的生成。這些“意外”往往是學(xué)生思維的亮點(diǎn),是學(xué)生創(chuàng)造性學(xué)習(xí)的體現(xiàn)。當(dāng)課堂出現(xiàn)“意外”時(shí),教師首先要理智面對(duì),然后通過(guò)適時(shí)追問(wèn)引導(dǎo)學(xué)生推進(jìn)思維的進(jìn)程,讓學(xué)生的獨(dú)特智慧得以激發(fā)。
[案例]《萬(wàn)以內(nèi)退位減法》教學(xué)片段
在教學(xué)《萬(wàn)以內(nèi)退位減法》一課時(shí),當(dāng)學(xué)生掌握了退位減法的計(jì)算方法以后,教師給學(xué)生設(shè)計(jì)了一組練習(xí)題,為了突破連續(xù)退位這一教學(xué)難點(diǎn),這一組題中有一道這樣的題: 10000-5678=?。
師:同學(xué)們,在計(jì)算10000-5678=?時(shí),你們是怎么算的。
一位學(xué)生結(jié)合自己的豎式講了自己的計(jì)算過(guò)程。
師:同學(xué)們,在做這一道題時(shí)一共進(jìn)行了幾次退位呀?
生:一共進(jìn)行了四次退位,并且都是連續(xù)退位。
師:是呀,我們?cè)谧鲞@一類題目時(shí)千萬(wàn)要注意不能忘記了退位,不然就錯(cuò)了。
這時(shí),突然有一個(gè)學(xué)生站起來(lái)說(shuō):老師,這一道題不退位也可以做呀,并且不容易錯(cuò)。
其他學(xué)生向這位同學(xué)投去了驚異的目光,并紛紛議論開來(lái),都表示這一道題不退位一定是錯(cuò)的。這時(shí),教師進(jìn)行了追問(wèn):那么你是怎么做這一道題的,能和大家說(shuō)一說(shuō)你的方法嗎?
生:在計(jì)算10000-5678=時(shí),我們可以先把這一道題看做9999-5678 ,這樣就不用退位了,9999-5678=4321,口算也可以算出來(lái),然后把4321+1就得到4322。這樣算起來(lái)又對(duì)又快。
此時(shí),其他學(xué)生恍然大悟。教師說(shuō):是呀,在做計(jì)算題時(shí)我們要盡量選擇簡(jiǎn)便的計(jì)算方法,這樣才能不會(huì)讓計(jì)算出錯(cuò)。這一堂課上,我們要特別感謝這一位同學(xué)給我們帶來(lái)的啟示,這個(gè)方法老師也沒(méi)有想到過(guò),確實(shí)很妙。這個(gè)方法使我們對(duì)“連續(xù)退位”的題目有了更深刻的認(rèn)識(shí)。現(xiàn)在,我們把最最熱烈的掌聲送給他,好不好。
以上案例中,當(dāng)一位學(xué)生出現(xiàn)“這一道題不用退位也可以做”這一意外時(shí),如果教師對(duì)這一意外進(jìn)行否定,或者通過(guò)“是嗎?我們下課時(shí)再交流”這類話語(yǔ)簡(jiǎn)單帶過(guò),就不會(huì)呈現(xiàn)出課堂的精彩了。課堂上,教師通過(guò)及時(shí)追問(wèn)的方式引導(dǎo)學(xué)生說(shuō)出了自己做這一道題目時(shí)的思維過(guò)程,使整堂課的教學(xué)目標(biāo)得到了升華。這一位學(xué)生富有創(chuàng)意的方法實(shí)質(zhì)上是一種轉(zhuǎn)化思想,轉(zhuǎn)化思想是一種重要的數(shù)學(xué)方法,在本堂課上通過(guò)這一位學(xué)生得到了精彩的演繹。
總之,課堂追問(wèn)是教師應(yīng)該掌握的一項(xiàng)教學(xué)基本功,也是一門教學(xué)藝術(shù)。在小學(xué)數(shù)學(xué)教學(xué)中,教師要把握時(shí)機(jī),通過(guò)有效追問(wèn)讓學(xué)生的思維之花得到綻放。

