算術與代數的區別與聯系

　　好的數學教師應當具有這樣一種專業素養，即是能夠跳出細節并從整體上把握自己的教學內容，如什么是這一學期、這一學年，乃至整個學段和整個小學學習期間的主要教學內容，教師在教學中并應努力做好“承上啟下”的工作。顯然，從這一角度去分析，弄清算術與代數（在此主要指初中代數——下同）之間的區別與聯系就特別重要，因為，自然數、分數與小數的認識以及它們的運算正是小學數學教學（更為準確地說，應是“算術”教學）的主要內容，而且，代數思想在算術教學的滲透，不僅直接關系到我們的算術教學能否真正做到“居高臨下”，對于學生順利地由小學過渡到中學也是十分有利的。當然，這也正是新一輪數學課程改革的一個明顯特點，即是將原先屬于初中代數的部分內容（負數和方程）下放到了小學，從而也就在這一方面提出了直接的要求。
　　
　　一、同與不同
　　
　　1．從總體上說，這顯然是算術與代數的一個重要區別，即有著不同的研究對象：算術主要集中于自然數、分數和小數的認識，包括相應的計算方法；代數的研究對象則不僅由具體的數擴展到了由字母和數字組成的（代數）式，也更加側重于方程的研究與應用。
　　當然，從形式上看，代數中關于式的研究又應說是與算術中關于數的研究較為接近的。具體地說，盡管運算的對象不同，其涵義也有所擴展，特別是引進了合并同類項、因式分解等新的運算，但在數的運算與式的運算之間顯然又有著直接的類比關系。更為重要的是，兩者似乎也有著共同的關注，即如何能夠通過適當的計算求得最終的結果。
　　也正是在這樣的意義上，一些學者提出：“算術在很大程度上是過程性的。”另外，這顯然也就是人們在算術的教學中何以特別重視算法的掌握以及計算的準確性和迅速性的直接原因。
　　然而，應當強調的是，如果我們對于式的教學采取完全相同的觀點，即是唯一強調如何能夠通過適當的計算求得所需要的結果，則就很可能因此而忽視了一個十分重要的代數思想：“代數即概括。”更為具體地說，這正是數學中引入字母的一個主要作用，即有助于人們通過概括達到更高的抽象層次。從而，如果我們在教學中只是強調了用字母去代表數，卻沒有能夠更加重視如何能夠幫助學生很好理解“概括”這樣一種重要的代數思想，就不能不說是忽視了在算術與代數之間所存在的這一重要區別。恰恰相反，我們應當清楚地認識到這樣一點：“概括也是學習代數的一個途徑。”
　　應當指出，上述的“過程性觀點”又不僅僅體現于數的運算，而且也直接影響到了人們對數的理解。例如，在筆者看來，我們就可從這一角度去理解學生在分數與無限循環小數的學習中何以會經常出現如下的困惑，如“0.999……與1究竟哪個大？”因為，這里的關鍵恰恰就在于觀念的必要更新，也即如何能夠幫助學生由過程性的“潛無限觀念”轉變到對象性的“實無限觀念”。
　　2．相對于式的教學而言，方程的認識與應用在代數的教學中顯然占有更為重要的地位，而也只有從后一角度去分析，我們才能更為深入地認識這樣一點：代數的學習必然要求學生超越上述的“過程性觀點”并達到新的更高的認識水平。從而，這也就應被看成在算術與代數之間所存在的又一重要區別。
　　具體地說，等量關系無疑應當被看成方程的本質，這也就是指，方程所強調的正是對象之間的等量關系。盡管 “解方程”的主要目的仍然在于如何能夠經由具體運算求得相應的未知量，但在這一過程中我們又必須特別注意不能因此而破壞方程兩邊的等量關系，也即變形后所得出的新方程應是與原來的方程等價的。例如，也正是在這樣的意義上，人們提出，“等價是代數中的一個核心觀念”。
　　由“等號”的不同理解我們即可更好地認識代數與算術在這一方面的重要區別：如果說等號的使用在算術中主要表明了運算的具體實施過程，也即由具體運算所依次得出的結果，那么，在代數中，“等量關系”就已成為等號的主要意義。例如，從這一角度去分析，我們就可立即看出，以下的常見錯誤主要就是因為學生仍然處于“過程性觀點”的直接影響之下：
　　3x=5+13=18=18÷3=6。
　　進而，我們在此又應明確提出關于“過程性觀點”（也可稱為“程序性觀點”）與“結構性觀點”的區別。例如，就字母與式的理解而言，所謂的“過程性觀點”就是指將字母或字母表達式看成所要求取的求知量的直接取代物，這也就是指，我們在此所關心的主要是如何通過具體計算求得所說的未知量；與此相對照，“結構性觀點”則是將字母或字母表達式看成直接的對象而非具體數量的取代物，我們在此所主要關注的也只是式與式之間的關系——從而，按照這樣的理解，符號表達式事實上就應被看成整體數學結構的一個組成成分。
　　值得指出的是，也正是遵循這樣的分析思路，一些學者明確提出了這樣一種觀點，即認為由“過程”到“對象”的轉變（這就是所謂的“凝聚”）可以被看成是代數思維的一個基本形式，我們并可從這一角度清楚地去指明在代數與幾何之間所存在的重要區別。
　　最后，應當強調的是，我們不應把“結構性觀點”與“過程（程序）性觀點”絕對地對立起來。恰恰相反，這正是數學思維的一個重要特點，即應當依據不同的情景和需要在“過程”與“對象”之間作出必要的轉換，包括由“過程”轉向“對象”，以及由“對象”重新回到“過程”。例如，在求解方程時，我們顯然必須將相應的表達式，如（x+3）2=1，看成單一的對象，而非具體的計算過程，不然的話，就會出現上述的“連等式”這樣的錯誤。然而，一旦求得了方程的解，如x=-2和-4，作為一種檢驗，我們又必須將其代入原來的表達式并實行具體的計算，從而，這時所采取的又是一種“過程”的觀點。
　　
　　二、聚焦教學涵義
　　
　　就代數思想在小學算術教學中的滲透而言，應當首先明確：這并非外部強加給小學數學教學的附加性成分，因為，小學數學的相關內容本身就包含了這些因素。例如，這事實上也就是在現今的數學教育研究何以會出現以下一些術語的主要原因，如“算術的內在代數本質” “早期代數思維” “涌現的代數”，等等。進而，又如“涌現”（emergence）這一詞語所清楚表明的，我們在此所提倡的正是一種自然而然的變化，也即如何能在算術的教學中自然而然地體現代數思維。以下就圍繞“概括”與“等價觀念”這樣兩個代數思想對此作出進一步的分析論述。
　　1．上面已經提到，字母的引入（更為一般地說，就是由數到式的過渡）應當很好體現“概括”這樣一種思想。例如，我們顯然就可從這一角度去理解以下的一些論述：“代數是概括的算術” “代數意義衍生于它的數字基礎” “概括也是學習代數的一個途徑”，等等。
　　進而，我們顯然也可從同一角度去理解以下研究工作的意義，特別是，這更可被看成為我們具體判斷學生的發展水平提供了可能的標準：就學生對于字母表達式的理解而言，可以大致地區分出這樣六個不同的水平：（1）賦予特定數值的字母：從一開始就對字母賦予一個特定的值；（2）對字母不予考慮：根本忽視字母的存在，或雖然承認它的存在但不賦予其意義；（3）字母被看成一個具體的對象：認為字母是一個具體物體的速記或其本身就被看成一個具體的物體；（4）字母作為一個特定的未知量：把字母看成一個特定的、但是未知的量；（5）一般化的數：把字母看成代表了或至少可以取幾個而不只是一個值；（6）字母作為一個變量：把字母看成代表一組未指定的值，并在兩組這樣的值之間存在有系統的關系。進而，以下的調查結果（這是1976年在英國實施的一項大規模的調查研究，其中共對3000名13~15歲的中學生進行了51項的筆試）顯然又可被看成更為清楚地表明了注意代數思想在算術教學中滲透的重要性：大多數學生（13歲中的73%，14歲中的59%，15歲中的53%）或是把字母當做具體的對象，或者根本就不去管它們。
　　
　　再者，就概括思想的具體學習而言，表格無疑具有特別的重要性。例如，這顯然也就是以下論述的一個主要意義：“表格可能是學習代數旅程的起點。”然而，這又是在現實中經常可以看到的一種弊病，即教師在教學中沒有給學生的主動探究留下足夠的空間，特別是忽視了關于圖像的視覺與實際操作應當被看成概括的必要基礎，從而就極大地“削減了概括過程的豐富性”。
　　更為一般地說，這事實上也就是眾多“找規律”課程的一個共同弊病：其所希望的即學生能夠按照教師（或者說，教材）的暗示、用教師（教材）指定的方法、并按照教師（教材）指定的步驟去作出所謂的“發現”。顯然，在這樣的情況下，學生的“主動探究”在很大程度上就只能說是一種“假探究”。
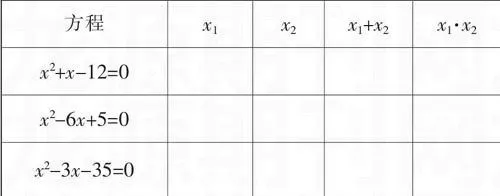
　　例如，以下關于韋達定理的教學設計在很大程度上就可被看成這樣的一個實例：
　　先讓學生填下列的表格，然后問：你認為一元二次方程的根與系數之間有什么關系？
　　2．盡管從教學的角度看以下的措施似乎都只是一種小技巧，即在教學中有意識地使用不同的字母、或是對已選定的字母作出改變，如將4x+7 = 35變形為4y+7 = 35，直至用更為復雜的符號表達式去取代原來的字母，如4x+7 = 35與4（2r+1）+7 = 35等，但這顯然十分有益于學生超出“外在形式的感知”從而也就能夠更為深入地去認識對象的內在數學結構。值得指出的是，這里所說的“外在形式的感知”事實上也正是學生在操作性活動何以經常出現某些“規律性錯誤”的一個重要原因。當然，我們在教學中又應注意引導學生對所說的不同表達式作出必要的比較，
　　另外，我們顯然也可從同一角度去理解以下一些教學設計的意義，即是如何能夠幫助學生初步地建立起關于“等號”的“結構性觀念”，而不只是認為“等號”表明“給出答案”（正因為此，等式也就常常被看成具有固定的“方向”：左邊表示應作的運算，右邊表示答案）：如教師在教學中可以有意識地讓學生構造這樣一些等式，先是每邊都有一個運算，如4+3=6+1，2×6=4×3，2×6=10+2等；接下來是每邊都有兩個運算的，隨后是每邊都有乘法的，如 7×2+3-2=5×2-1+6，等等。
　　更為一般地說，以下正是學生形成關于方程的“結構性觀念”的一些關鍵環節：（1）用字母代表數；（2）等號表示左、右雙方的等價性；（3）右邊的項不一定是單一的數而也可能是一個代數式。從而，這也就十分清楚地表明這樣一點：小學數學教學確實能在這一方面發揮更大的作用，也應發揮更大的作用。
　　更為具體地說，這應當被看成小學數學教學的一項重要目標，即努力促進學生由“過程性觀念”向“結構性觀念”轉變。值得指出的是，從這一角度去分析我們也可更為深入地認識“奧數”的盛行對于數學教學的嚴重影響：由于在小學奧數的訓練中，方程幾乎無一例外地只是作為一種新的解題方法得到了介紹，學生對于方程方法的應用又常常依賴于記憶與模仿。因此，這種學習恰恰就是丟掉了代數學習中最為根本的一些東西，由此所形成的“思維定式”也必然會對學生將來的數學學習產生嚴重的消極影響。
　　在筆者看來，后一實例事實上并就進一步證實了筆者對于當前普遍存在的學生“兩極分化”現象的如下判斷：“所謂的‘超前教育’正是造成現今‘兩極分化’的一個重要原因，這也就是指，我們所看到的事實上并非真正的‘優秀學生’與‘差生’之間的差距，而是由各種原因造成的‘提前起跑者’與‘正常起跑者’之間的差距。而且，這里所說的‘先進生’有很多不僅不能被看成真正的優秀學生，更可能是一個‘越做越恨’ ‘越學失敗感越強’，甚至靈魂也因此受到一定扭曲的‘偷跑者’。”
　　
　　三、更為一般的分析
　　
　　1．依據上述分析，我們也可更為深入地去理解什么是“過程教育”的主要涵義，特別是，什么是真正的數學活動，什么又是學生在數學學習中的適當活動？
　　具體地說，這是筆者在這一方面的一個基本觀點：我們應當清楚地認識數學活動的豐富性。例如，上面已提到的概括、抽象、符號化、視覺化、操作、算法的應用等顯然都應被看成學生數學活動的重要形式，除此以外，我們還可以提及下定義、綜合、表征、證明和公理化等活動。
　　其次，同樣重要的是，相對于外在的形式而言，我們又應更加重視內在的數學思維，也即應當十分重視通過具體的數學活動幫助學生學會數學地思維。例如，從這一角度去分析，就代數思維向小學數學的滲透而言，字母的使用就不是真正的關鍵，因為，就如以下的論述所清楚表明的：“低年級的代數思維涉及在活動中培養思維方式，字母—符號代數可以作為工具被應用于這些活動中，但是這些活動并非排除代數，而且在根本不使用任何字母—符號代數的情況下，學生可以參與到這些活動中，比如，分析數量之間的關系、注意結構、研究變化、歸納化、問題解決、模式化、判斷、證明和預測。”
　　更為一般地說，這事實上也可被看成“關于算術教學的現代觀點”的核心所在：“算術不（應）僅僅關注計算能力，它還應該通過數學知識活動，為學生提供機會，以便于他們奠定一個堅實的數學傾向的基礎。通過簡單的例子，理解數學陳述與它們所模擬的情境（或者沒有模擬）之間的關系，學習猜想、論證（或多或少是非正規的）和證明（如在數字理論領域）的藝術，甚至從理想的角度來看，意識到作為‘數字’意義的激進的概念結構化的本質正在得到逐步的擴展。”
　　另外，在筆者看來，上述觀點也為我們究竟應當如何去理解所謂的“數感”（眾所周知，這是新一輪數學課程改革的一個明確主張，即應將“培養與發展學生的數感”作為數學教學的一項重要目標）提供了直接啟示。后者即是指，盡管我們在此所使用的是“數感”（the number sense）這樣一個詞語，但這又不被理解成僅僅局限于“數的感知”這樣一個范圍，毋寧說，就如對于“外在形式的感知”的必要超越，我們在此也應積極引導學生更為深入地去認識研究對象的內在數學結構。當然，由所做的分析我們也可清楚地看出，“數感”不應被看成先天的才能，而主要依賴于后天的學習。
　　2．除去算術與初中代數的（區別和）聯系以外，我們顯然也應從同一角度去看待初中代數與高中代數（乃至抽象代數之間）的聯系。例如，上述對于“數學結構”的強調就正是現代數學研究最為基本的一個思想。另外，在筆者看來，我們顯然也應從同一角度去理解以下的論述：“代數不僅僅成為關于方程和解方程的研究，也逐步發展成涵蓋函數（及其表征形式）和變換的研究。”又，“函數方法……不僅擴大了代數的內容，而且也被用來設計和解釋研究的理論觀點和技術觀點，這增加了意義源泉分析的復雜性。”
　　綜上可見，在算術的教學中我們就應積極地去滲透這樣三個代數思想：第一，概括的思想；第二，等價觀念；第三，變化與函數的思想。當然，就這方面的具體工作而言，我們又應高度重視與學生的思維發展水平相適應。
　　最后，筆者以為，上述分析事實上也為我們如何更為深入地去理解關于“數學教學的整合觀點”提供了重要啟示，后者即指，這不應唯一地被理解成不同數學分支的適當整合。恰恰相反，我們應當更加重視如何能夠跳出小學與初中的教學范圍并從更為宏觀的角度去進行分析思考，從而真正發展起一種“內在一致的、綜合性的理論框架”。容易想到，這也正是《數學課程標準》的制定與修改所應特別重視的一個問題。