談教學情境設置的學科特性

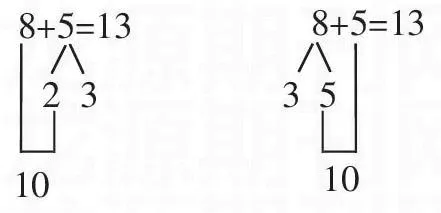
　　情境設計
　　策劃人語：教學情境是課堂教學的基本要素。創設良好的教學情境既是課程改革的重要理念，又是教師從事教學活動不可或缺的專業能力。
　　學科特征是教學情境的本質屬性。教學情境的創設，必須以達成學科教學目標為出發點，應能體現學科應有的“學科味”；應能體現知識的發生、形成和發展過程；應能體現學科知識在實際生活中的價值，幫助學生準確理解學科知識的內涵：應是所學知識在現實的、有挑戰性的一個事物或場景。總之，教學情境的創設既要為學生的學習提供認知的基點，又要激發學生的學習心向，達到促進學生有效開展學習活動的目的。
　　圍繞教學情境的創設廣大教師開展了許多有價值的課題研究，如“情境教學如何體現學科本質”“情境教學與學科特征”（情境教學的意義和作用”“情境教學的理論依據和基本途徑”“情境教學的原則和策略”等等。本期欄目的兩篇文章均以數學學科為例，圍繞情境教學如何體現學科本質、凸顯學科特征這樣一個核心進行了深度的探討。
　　還有其他學科的更多相關課題期待廣大教師共同參與研究，非常歡迎將研究成果投與本刊。（袁玉霞）
　　
　　所謂教學情境是指在教學活動中為實現教學目標而營造的具體場景或氛圍。現代課程觀認為，教學情境是課堂教學的基本要素。為完成教學任務創設一定的激發學生認知經驗，喚起學生認知情感的良好氛圍，已成為了一線教師落實新課程理念的基本策略。然而在實踐中，許多教師在設置教學情境時，過于追求趣味性、情節性、生活化等元素，忽視情境的學科性、問題性等本質要素，造成盲目使用情境、選擇教學情境不當的現象屢有發生。下面以數學學科為例，就教學情境設置如何凸顯學科性談一些想法和做法。
　　先看一位教師在《求簡單平均數》教學中的一個片段：
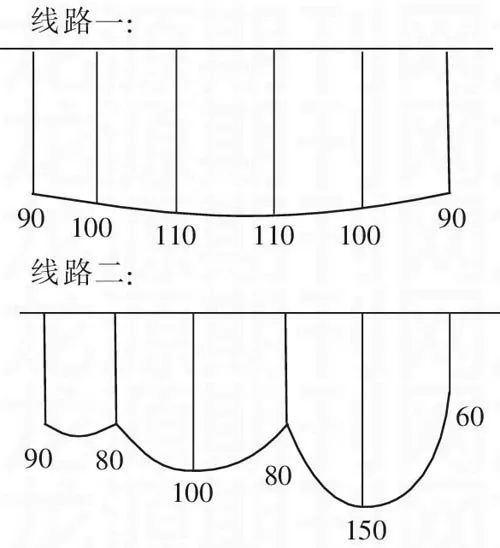
　　師生談話回顧“小馬過河”的故事后，媒體呈現兩張線路圖。小馬從哪一條路走，能過這條河？（注：小馬的身高為120厘米）。
　　對學生而言，這是一個感興趣的情境。課堂上，他們圍繞小馬能否過河展開了激烈的討論。有的說第一條路能過，第二條路不能過；有的說兩條路都能過，第二條路深的地方小馬跳一下就能過去；還有的說兩條路都不能過，因為小馬會陷在泥里的……學生在過河方法的爭論上，花了很長的時間，對情境中所隱含的數學內涵卻沒有關注。這當然與教師的調控不無關系，但根本原因則與教師設置的教學情境缺乏針對性（一在年齡上，二在內容上）有關。對于這節數學課來說，這當然是一次失敗的情境設計。筆者以為，一個高質量的數學教學情境，圍繞數學學習展開是其基本特征。也就是說，數學教學情境的設置，必須是以達成數學教學目標為出發點的，始終圍繞數學知識技能的獲取和數學素養的培養來進行，體現數學味，突出數學學科的本質特點。那么怎樣的教學情境才是具有數學學科特性的呢？實踐中我們又該如何來設計呢？現從以下三個方面加以闡述。
　　
　　一、數學問題是數學教學情境的基本要素
　　
　　實踐表明，有價值的教學情境一定內含問題。數學教學情境，當然應該含有數學問題，并且圍繞數學問題展開。如一位教師在執教《握手中的數學問題》這節課時設置的教學情境：
　　師：兩個老同學見面一人握一次手，握了幾次手？
　　生：1次。
　　師：四個老同學見面每兩人不重復地握一次手，可以握幾次？
　　學生有不同回答。教師請學生以四人小組為單位進行體驗后統一意見：6次。
　　師：那么我們班40個小朋友這樣握手，可以握幾次？
　　學生茫然。
　　師：你們可以猜猜看。
　　出現了多種答案：80次，58次，420次，160次，140次……
　　這是一個典型的數學情境，很有數學味。情境中提出了一個本節課學習的基本數學問題：40個小朋友不重復，每兩人握一次手，可以握幾次？這個問題一則有激起學生探究欲望的作用；二來也為探究活動的展開明確方向。因為一下子解決40個小朋友握手次數的問題比較困難，根據同樣的提問方式，可以轉化為研究2個人、3個人、4個人、5個人……握手次數的問題。顯然，正因為有這樣一個引發學生思考的數學問題的存在，使教學情境體現了濃濃的數學味。那么，怎樣的問題才是凸顯數學教學情境的學科特性的呢？這需要結合數學學科教學的任務來思考。數學課上的教學情境，應其具有承載數學學習內容的功能。因此，情境中所蘊含的問題也需有利于促進學生的數學學習，一般具備兩個方面的特征：
　　1．問題是現實的、有意義的
　　數學教學情境中的問題是否現實、有意義，將直接影響到學生原有數學學習經驗的呈現和對教學內容實質的把握，影響到學生進行“觀察、實驗、猜測、驗證、推理與交流等數學活動”的有效性。筆者認為，現實的、有意義的數學問題有利于激發學生的探究興趣，有利于學生展示已有的認知基礎，為教師進一步引導提供策略選擇上的依據。
　　上例中教師提出數學問題是學生在生活中能夠感受得到的，與本班學生實際相聯系又有利于激起學生探究的興趣。同時，也是有意義的，因為在對情境的初步領會和理解中，學生原有思維水平能夠比較清晰地呈現出來：對象較少時，學生能夠知道“握手”的次數；對象較多時，則會有困難。
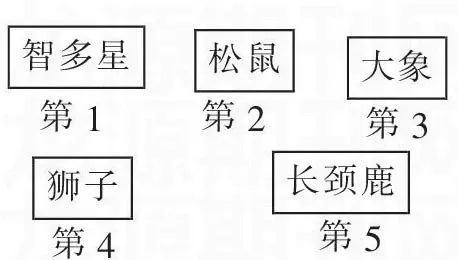
　　當然，這里所說的“現實”不只是指學生生活中的所見所聞，也應該包括他們在數學或其他學科學習中能夠思考或操作的，屬于思維層面的現實。如“第幾”這節內容，一位教師在教學中設置了這樣一個教學情境：
　　學生把5只小動物排成一隊：智多星排在最前面，小松鼠排在第二個，大象排在第三個，獅子排在第四個，長頸鹿排在最后面。教師順著學生的敘述及時板書成：
　　提出問題：假如今天也讓你去參加音樂會的話，你準備排在哪里？學生答：我準備排在第三個。問：你排第三個了，那么其他的小動物排哪里呢？答：智多星、小松鼠不變，大象排第4，小獅子排第5，長頸鹿排到第6了。
　　這里雖然借助了一個童話故事作為教學情境，但它是富有現實意義的。因為對學生來說，如何“排隊”是他們經歷過的，教師正好借助學生的經驗來讓學生體會：排在最前面的可以稱為“第一”，排在第一后面的叫“第二”……依次類推。可見，這個教學情境既體現了問題的現實性，又包含有豐富的數學價值；既有利于激起學生思考的積極性，又有利于學生切實展開探究活動。
　　2．問題是豐富的、有層次的
　　具有普遍意義的數學結構一般是在對多個具有相關特質問題的研究后歸納得到。因此，數學教學情境中的問題也應該是豐富的、有層次的。只有有層次的數學問題，才能引導學生在對“問題”的研究中抽象出具有本質同一性的數學規律或數學方法。如在“握手問題”中，教師僅從2人、4人握手的情況中引導學生得到計算方法“人數×（人數－1）÷2”是不夠的，需要從對2人、3人、4人、5人甚至更多人握手的問題情境的研究中得出才對學生有說服力。
　　以下是一位教師在執教《分數的意義》時設置的教學情境，比較典型地體現了教學情境設置的層次性特點：
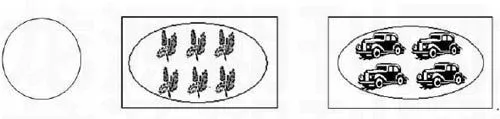
　　課始提供以下學習材料：
　　提出要求：請用以上材料，表示出一個分數，并說說這個分數所表示的意義。
　　學生用圓表示的分數有：1/4，7/16，3/16；用樹葉圖表示的分數有：1/6，2/6，5/6，1/2，1/3，2/3；用汽車圖表示的分數有：1/4，3/4，1/2。
　　教師結合學生的說明，把分數與相對應的圖呈現在黑板上，引導學生觀察歸納出分數的意義。
　　細細推敲，這三份材料體現著教學過程的三個層次：層次一，用圓表示分數，是單個平面圖形，一則幫助學生回憶分數的產生過程，二來讓學生說說相關分數的意義，了解學生原有的認知水平，以便在下一環節中選擇恰當的教學策略；層次二，用6棵樹圖表示分數，嘗試探究，初步理解單位“1”的意義，完善對分數意義的理解；層次三，用汽車圖表示分數，進一步豐富學生的表象，強化對單位“1”及分數意義的理解。三個層次的學習均圍繞“分數意義”的本質展開，引導學生經歷“分數”在單個圖形到一群物體中產生的過程，切實把握分數的本質內涵，即把單位“1”平均分成若干份之后其中的一份或幾份。這樣的教學情境才是高質量的，有成效的。
　　
　　
　　二、數學教學情境需蘊含數學知識的內在結構
　　
　　數學學習不僅是對數學知識的習得，更是數學思想方法的形成與掌握。數學教學情境的設置，不僅需要為學生習得數學知識服務，更要為激發學生思考、形成數學素養服務。因此，數學課上，設置的教學情境，除了蘊含數學問題之外，還應該體現數學知識的內在結構，為學生在數學學習過程中理解數學原理、掌握數學方法提供必要的支持。如有位老師在教學《20以內進位加法》時，提供了以下的情境（如下圖）：
　　老師引導學生觀察情境圖，初步了解信息，提出“一共有多少個雞蛋”的問題，讓學生嘗試解答后，有學生列出了8＋5＝13的結果。接著有以下的對話：
　　師：你是怎么算出答案13的？
　　生：8與10相差2，5里面有2，把2分到8這里去就是10了，還多3個，就是13。
　　師：剛才這位同學說的是什么意思？
　　生：只要把左邊擺成10個，右邊就剩下3個，一看就知道是13。
　　教師根據學生的解釋，板書如下左圖。
　　師：還有沒有別的方法也能算8＋5？
　　生：把8分成3和5，5加5等于47b5de7788b256fc2636cb8dcbbc4e8f2f8622a663cdd875e42b73583238411710，再加上3就是13（如上右圖）。
　　顯然，設置“拿雞蛋”的教學情境，不僅是一個提出數學問題的過程，更是一個有利于引導學生呈現“湊10法”思考過程的情境（兩個盒子的結構有直觀呈現“湊10法”的作用），是一種情境蘊含數學結構的典型體現。
　　再如，在教學《用除法兩步計算解決問題》的內容時，設置了一個“書架擺書”的教學情境（如上右圖）。此情境不僅包含的數學信息相當豐富，而且又蘊含著數學知識的內在結構。在解決“平均每個書架每層擺幾本書？”這個本節課的重點問題時，學生有三種不同的解法：①90÷6÷3；②90÷（6×3）；③90÷3÷6。而這三種解法，均能通過圖形來作出解釋。解法①是先解決每個書架擺書的本數，再求出每層擺書的本數；解法②是先解決6個書架總的層數，再求出每層擺書的本數；解法③則是先解決總的一層擺的本數，再求出每層擺的本數。教學中，教師結合學生的解釋在圖中相應地作標注，學生的思維只需作適度的調整即可，便很容易理解相關的解法了。這與情境中的學習材料具體數學結構有關，這樣的教學情境正是數學課中所需要的。
　　
　　三、數學教學情境應為提升學生數學思考能力服務
　　
　　數學是思維的體操。培養學生的思維能力，讓學生學會數學地思考，是小學數學教學的一個重要內容。因此，誘發數學思考，啟迪學生思維也應該是設置數學教學情境的出發點。在教學《長方體的認識》這節內容時，教師設置了一個讓學生“搭長方體”的教學情境：用小棒搭一個長方體，請你思考一下，要幾個接頭？幾根小棒？小棒的長度有什么要求？學生思考后（不交流），請學生觀察教師提供的學具（提供的材料中有缺接頭的，也有缺小棒的），思考：提供的材料能否搭出長方體？抓住搭不出的，請學生說說問題在哪里？
　　情況一：不夠12根小棒的組（因為邊不夠，搭不出）。
　　情況二：12根小棒不能分成三組（搭出來后有的“面”不是長方形）。
　　交流分析得出：搭一個長方體，需8個接頭（即八個頂點）；12根小棒（即12條棱），每4根相等的為1組，分3組。在此基礎上繼續引導：剛才4根一組的小棒分別搭在哪里了？從而得出：相對4條棱的長度相等。
　　從實際的教學效果來看，因為“搭”這樣一個教學情境中，學生沒有具體的操作過程，而是通過想象、思考等思維層面上的活動來完成任務，這里需要較高的思維水平，對促進學生的思維比較有利。課堂上也正是以這樣的效果呈現出來的，先確認需要12根，又討論這12根需要分成3組，又利用搭不成功的小組討論3組4根小棒相對4根相等時才能搭成功。三個問題解決的過程，正是學生對長方體“棱”的特征準確把握的過程。這也正是設置本教學情境所希望看到的教學效果。
　　總之，教學情境只是一種教學載體，若想通過教學情境的展開來實現相關學科的教學目標，則需要教學情境必須具備相關學科的學科性。