對2011年全國數學高考理科第21題的深入探究
——兼談圓錐曲線的一個統一性質

● (漾濞縣第一中學 云南大理 672500)

對2011年全國數學高考理科第21題的深入探究
——兼談圓錐曲線的一個統一性質

●秦慶雄范花妹(漾濞縣第一中學 云南大理 672500)

2011年全國數學高考理科試題Ⅱ大部分都是比較常規的問題，但平凡中蘊含著不平凡，譬如第21題：

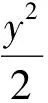
(1)證明：點P在C上；

(2)設點P關于點O的對稱點為Q，證明：點A，P，B，Q在同一圓上．

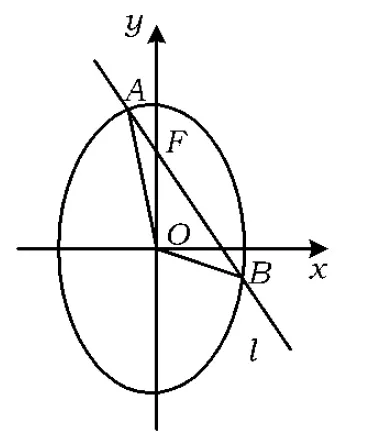
圖1

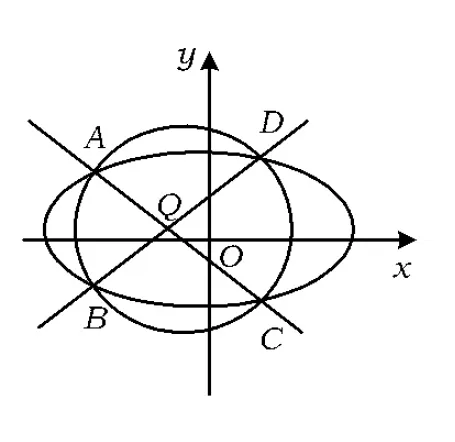
圖2

本題是一道解析幾何試題，設計新穎，綜合性強，集中考查了多個知識點，是一道有較好區分度的試題，值得深入探究.若將第(2)小題推廣為一般問題進行探究，則可獲得如下定理：

定理圓錐曲線2條相交弦的4個端點共圓的充要條件是這2條相交弦的斜率互為相反數.

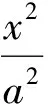
(充分性)若kAC=-kBD，設直線AC的方程為mx+ny+c1=0,則BD的方程為mx-ny+c2=0.

因為A,B,C,D是橢圓b2x2+a2y2-a2b2=0與2條相交直線AC,BD的交點，所以可設過點A,B,C,D的二次曲線系方程為:

(mx+ny+c1)(mx-ny+c1)+

λ(b2x2+a2y2-a2b2)=0(λ為參數),

整理得

(λb2+m2)x2+(λa2-n2)y2+m(c1+c2)x+n(c2-c1)y+c1c2-λa2b2=0.

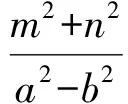
(必要性)若點A，B，C，D共圓，如果kAC≠-kBD，那么過點A作割線AE，使AE與CD相交且kAE=-kBD.由充分性知，點A,E,B,D共圓，因而點A,E,B,C,D共圓.又因為任何一個圓與橢圓不可能有5個交點,所以必有kAC=-kBD．

對于雙曲線和拋物線，可仿照橢圓的證明方法完成，這里從略．

因此，圓錐曲線2條相交弦的4個端點共圓的充要條件是這2條相交弦的斜率互為相反數.

如果掌握了上述定理的思路和方法，那么圓錐曲線的一些四點共圓問題便迎刃而解，下面舉例說明．

例1的證明過程如下：

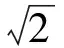
由于點A,B是直線l與橢圓C的2個交點,從而

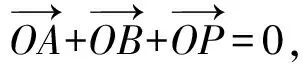
(x1+x2+x3,y1+y2+y3)=(0,0),

即

x3=-(x1+x2),y3=-(y1+y2)，

于是

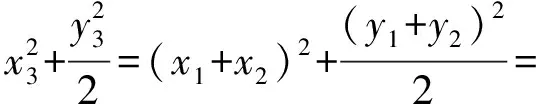
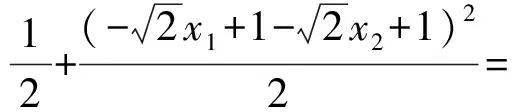
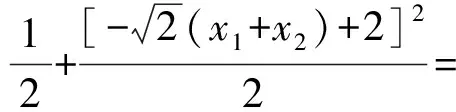
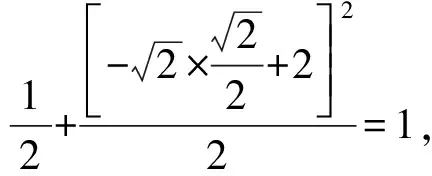
因此點P在橢圓C上.

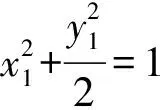
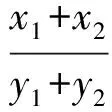
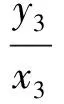
從而

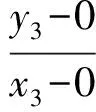
因此弦AB,CD相交且斜率互為相反數,由定理可知點A，B，C，D在同一圓上.