高維歐氏空間中向量的外積

夏盼秋

（武漢大學數(shù)學與統(tǒng)計學院，武漢 430072）

高維歐氏空間中向量的外積

夏盼秋

（武漢大學數(shù)學與統(tǒng)計學院，武漢 430072）

指出了對高維歐式空間中向量外積定義的不足，從幾何空間中向量外積的幾何描述入手，經(jīng)過簡潔的證明推導，重新提出了高維歐式空間中向量外積的定義，并得出了若干相關結論.

高維歐氏空間；向量外積；幾何描述；行列式

1 引 言

外積是線性代數(shù)中一個重要的概念，它最初源于對物理學中力矩等物理量的描述.經(jīng)過數(shù)學的嚴格推導證明，幾何空間中向量外積運算已成系統(tǒng)，并發(fā)揮著不可或缺的重要作用.同時，人們一直嘗試著將向量外積運算推廣至高維歐氏空間，最終給出了確切的行列式表達，且已將高維歐式空間下的外積運算成功地應用于數(shù)學以及其它領域［1-3］.然而這些工作忽略了向量外積運算的幾何意義，而更著重于高維歐式空間中向量外積的應用.必須注意，幾何空間中向量外積運算具有明確的幾何含義，那么對于推廣的外積運算是否同樣滿足推廣的幾何含義，以及一些相關問題的探討還是十分必要的.基于此，本文參照幾何空間里向量外積的定義，重新給出高維歐式空間中向量外積運算的定義，并得出一些相關結論.

2 高維歐式空間中向量外積定義的提出

幾何空間里向量外積的定義如下：

定義1 兩個向量α1與α2的夾角為ω（0≤ω≤π），則α1和α2的外積也是一個向量，記為α1×α2，其長度為

其方向垂直于α1和α2組成的平面，并且α1，α2和α1×α2構成右手系［4］.

由上述定義很容易得出兩條在幾何空間下與外積有關的性質：

設α1與α2線性無關，則

i）α1×α2的長度等于以α1，α2為鄰邊的平行四邊形的面積；

ii）α1×α2的方向垂直于α1，α2張成的平面.

由此可以猜想：n維歐氏空間下n-1個向量的外積大小等于這n-1個向量張成的平行多面體的體積，方向垂直于這n-1個向量張成的n-1維線性流形.由上面定義可知，幾何空間下的向量外積的方向由右手系確定.但在高維空間下無法應用類似于幾何空間的右手系定義.只有回避右手系定義，才能得到高維歐式空間下外積向量的完整定義.我們知道，幾何空間兩向量外積的另一等價定義——行列式定義，能否從行列式定義出發(fā)，得到高維歐式空間下外積向量的完整定義呢？為此，引入幾何空間兩向量外積的等價定義——行列式定義：

定義2 設O；i，j，

［k］是一個右手直角坐標架，α1和α2在其中的坐標分別是

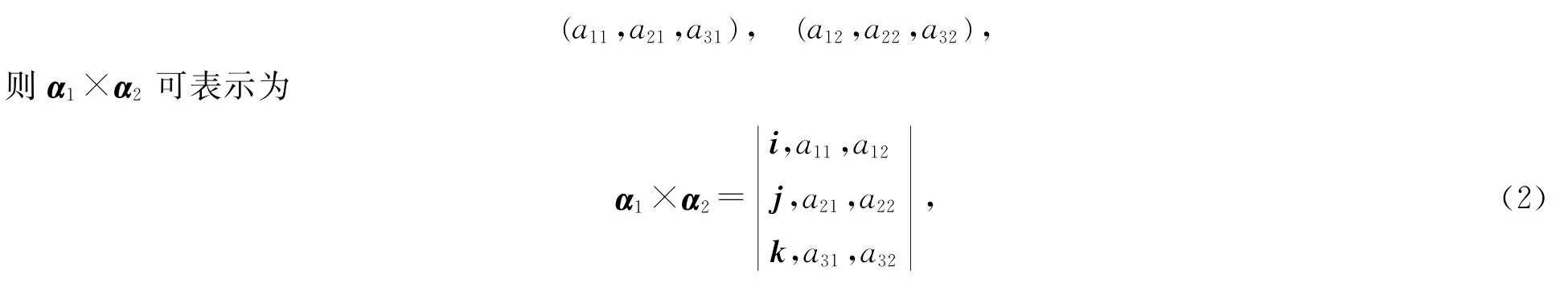
實際上，上述兩種有關幾何空間下向量外積的定義等價［4］.由定義可知，幾何空間下外積向量的方向由成右手系的標準正交基確定.

由此定義，如果借用歐氏空間的一個標準正交基來確定高維歐氏空間下的向量外積的方向定向，那么就可回避幾何空間下向量外積滿足右手系的要求.因此，只要找到不同基下外積向量的聯(lián)系與區(qū)別，就能得到n維歐氏空間下向量外積運算的幾何描述.即完整的n維歐氏空間下向量外積運算的定義.

下面給出n維歐氏空間下向量外積運算的定義.

定義3 設ξ1，ξ2，…，ξn是n維歐氏空間的一個標準正交基，向量η1，η2，…，ηn-1在這個基下的坐標為

顯然，上述行列式定義為幾何空間下向量外積的行列式定義直接推廣.如果能證明它滿足于幾何空間外積運算幾何性質的推廣，那么我們就得到了完整的高維歐氏空間下的向量外積定義.

事實上，?i＝1，2，…，n-1，因為

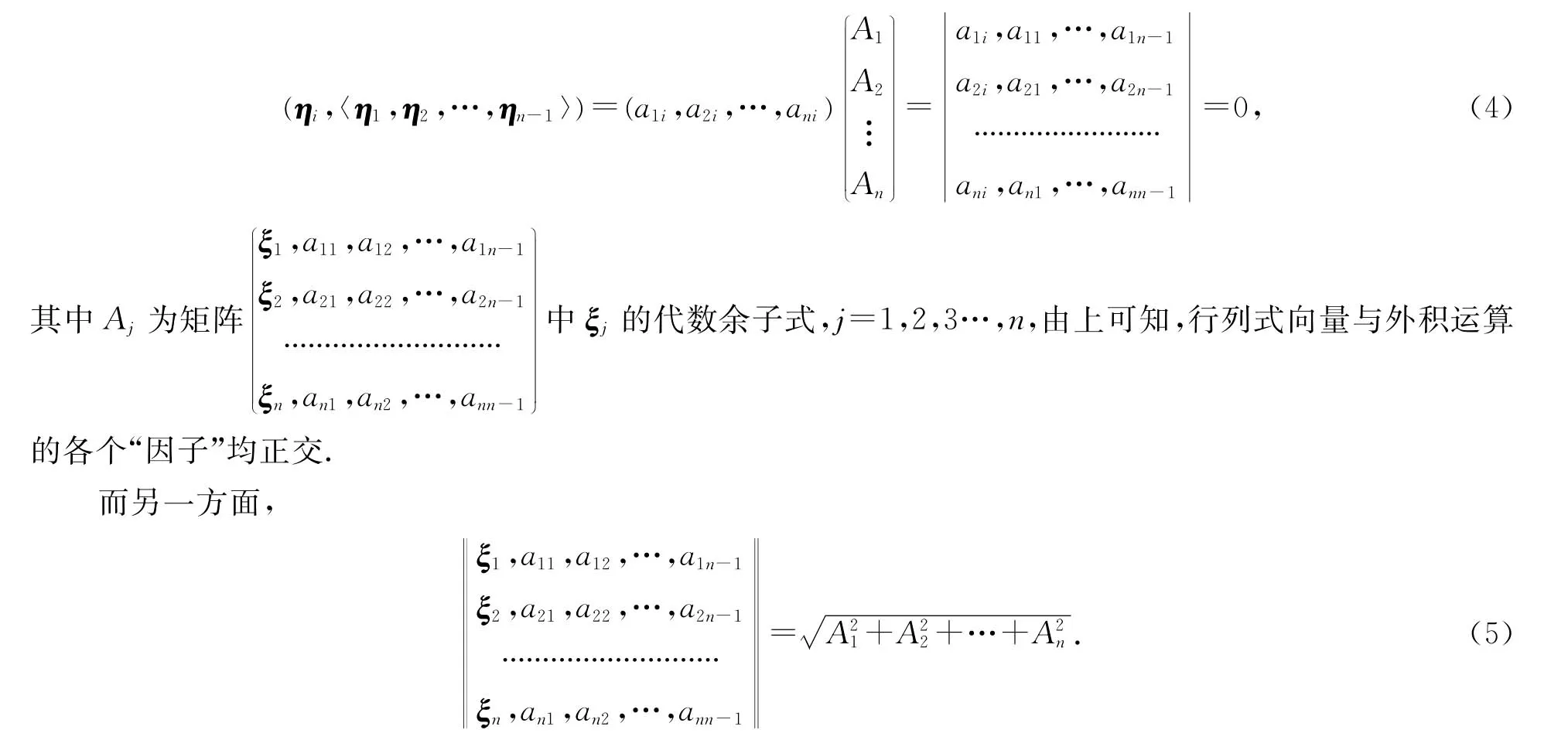
若向量η1，η2，…，ηn-1線性相關，那么體積為零，且對于所給外積行列式向量也有A1＝A2＝…＝An，即行列式向量的模等于η1，η2，…，ηn-1張成的平行多面體的體積；若它們線性無關，則可求得由向量η1，η2，…，ηn-1張成的平行多面體的體積.

先添加一個向量

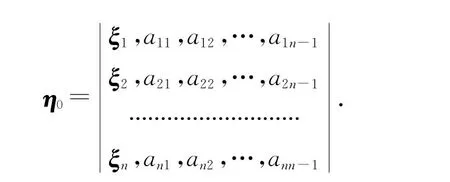
由于已證η0與η1，η2，…，ηn-1張成的n-1維空間正交，因此令η0，η1，…，ηn-1張成的n維平行多面體的體積為Vn，η1，η2，…，ηn-1張成的n-1維平行多面體的體積為Vn-1，則有以下等式成立：

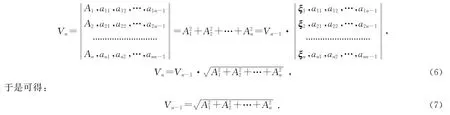
這樣，就已經(jīng)證明了定義3所給的行列式表示滿足幾何空間外積幾何定義的推廣.

3 若干結論

下面來討論不同基向量的選取對外積運算的影響.

定理1 n維歐氏空間下的n-1個向量，在不同標準正交基下的外積大小相等，方向相同或者相反，且兩個標準正交基之間的變換若為第一類正交變換，相應的外積方向相同；若為第二類正交變換，則方向相反.

證在給定的n維歐氏空間Vn里，任取兩個標準正交基：α1，α2，…，αn及β1，β2，…，βn，它們之間對應的正交矩陣為T，即

是Vn中n-1個線性無關向量，且在基α1，α2，…，αn下的坐標為

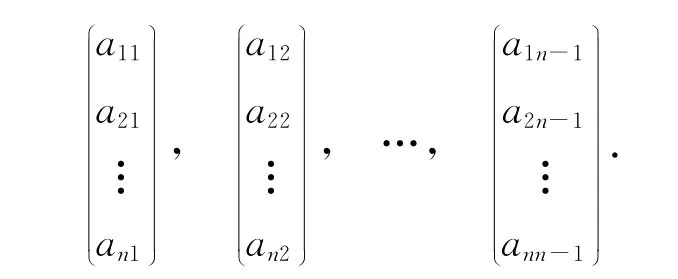
那么它們在基β1，β2，…，βn下的坐標為

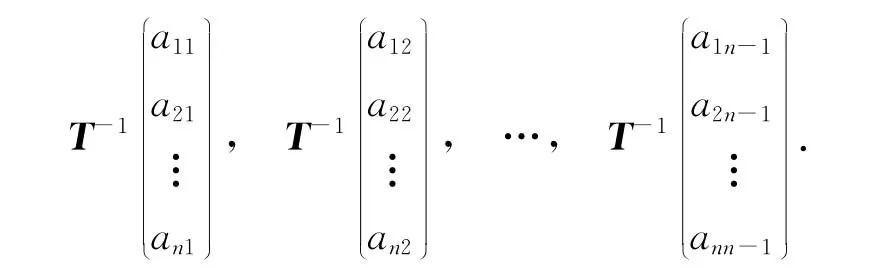
根據(jù)向量外積的行列式表達，可以得到〈η1，η2，…，ηn-1〉在兩個基下的行列式表達分別為

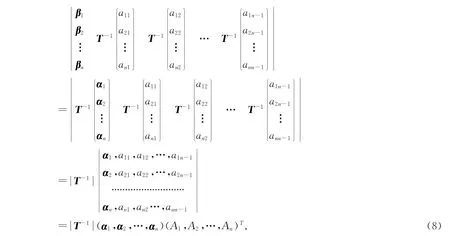
由此不難看出，基變換可以改變外積運算的結果.但是由于基向量的選取要求是標準正交基，則對分別應著第一、二類正交變換，且第一類正交變換不影響外積運算結果，第二類正交變換則使外積運算結果反向.

下面討論高維歐氏空間向量外積的性質.

線性性質：

定理2 n維歐氏空間下的外積運算滿足線性性質，即

已知n維歐氏空間Vn的一個標準正交基ξ1，ξ2，…，ξn，而η1，η2，…，ηn-1是Vn里一組線性無關向量，那么

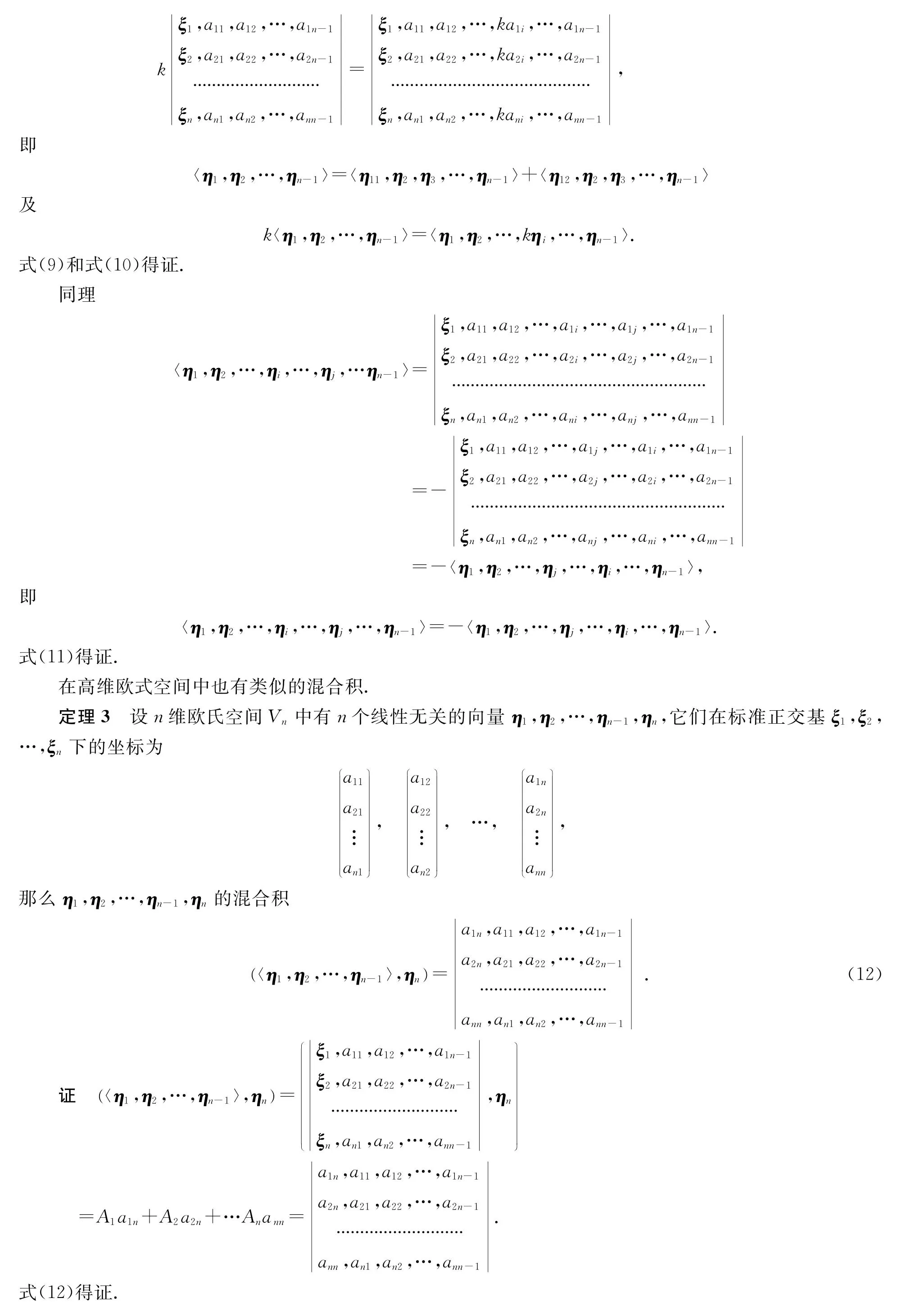
致謝 在成文過程中，得到了武漢大學樊啟斌教授的悉心指導，謹此致謝！

［1］ 李鴻祿.高維歐氏幾何學［M］.北京：原子能出版社，1996.

［2］ 張沛和，周瑜.R Rn空間的矢量積及其應用［J］.嘉應大學學報，2000，3：5—9.

［3］ 吳成茂.歐氏空間中一種外積定義的拓廣及其應用［J］.西安郵電學院學報，1997，2（4）：37—41.

［4］ 陳志杰.高等代數(shù)與解析幾何［M］.北京：高等教育出版社.

The External Product in Higher Euclidean Space

XIA Pan-qiu
（Wuhan University，Wuhan 430072，China）

The paper pointed out the lack of the definition for exterior product in higher Euclidean space.Starting from the geometric describing of external product in geometric space，after tersely attesting and deriving，writer represents the definition of the external product in higher Euclidean space outside and results some conclusions.

external product；higher Euclidean space；geometric describing；determinant

O183.1

C

1672-1454（2011）04-0159-06

2008-10-23；

2009-03-09