一道數學競賽題的一般形式

潘 杰， 周 玲

（合肥工業大學數學學院，合肥 230009）

一道數學競賽題的一般形式

潘 杰， 周 玲

（合肥工業大學數學學院，合肥 230009）

介紹浙江省2008年高等數學競賽一道二重積分的一般形式，分別利用化累次積分法、變數替換法、等值線法給出不同的證明.

數學競賽；二重積分；累次積分；變量替換；等位線法

2008年浙江省高等數學競賽（理工類）試題的第三大題為

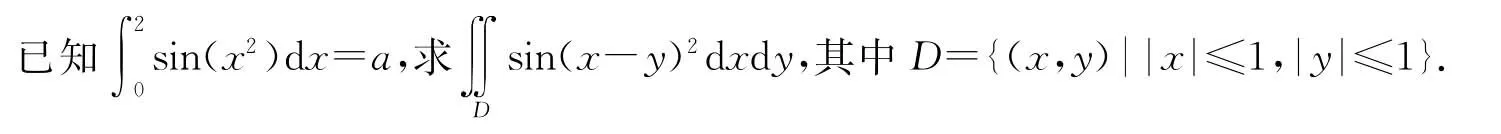
本文介紹這道試題的一般形式及其多種證法.

設f（t）為連續函數，則有

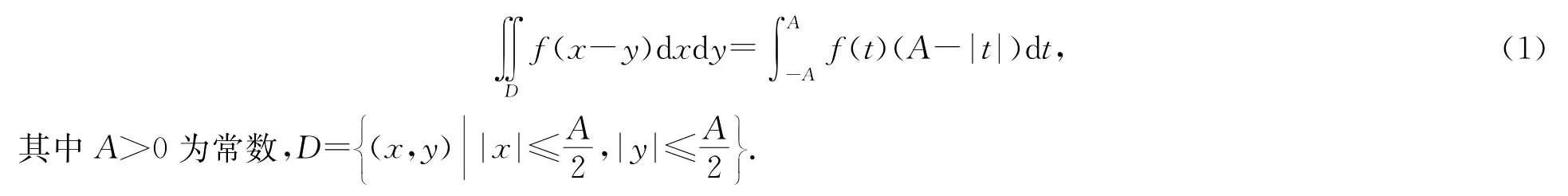
證法1 先將二重積分化為累次積分，利用變量替換并交換積分順序進行證明.

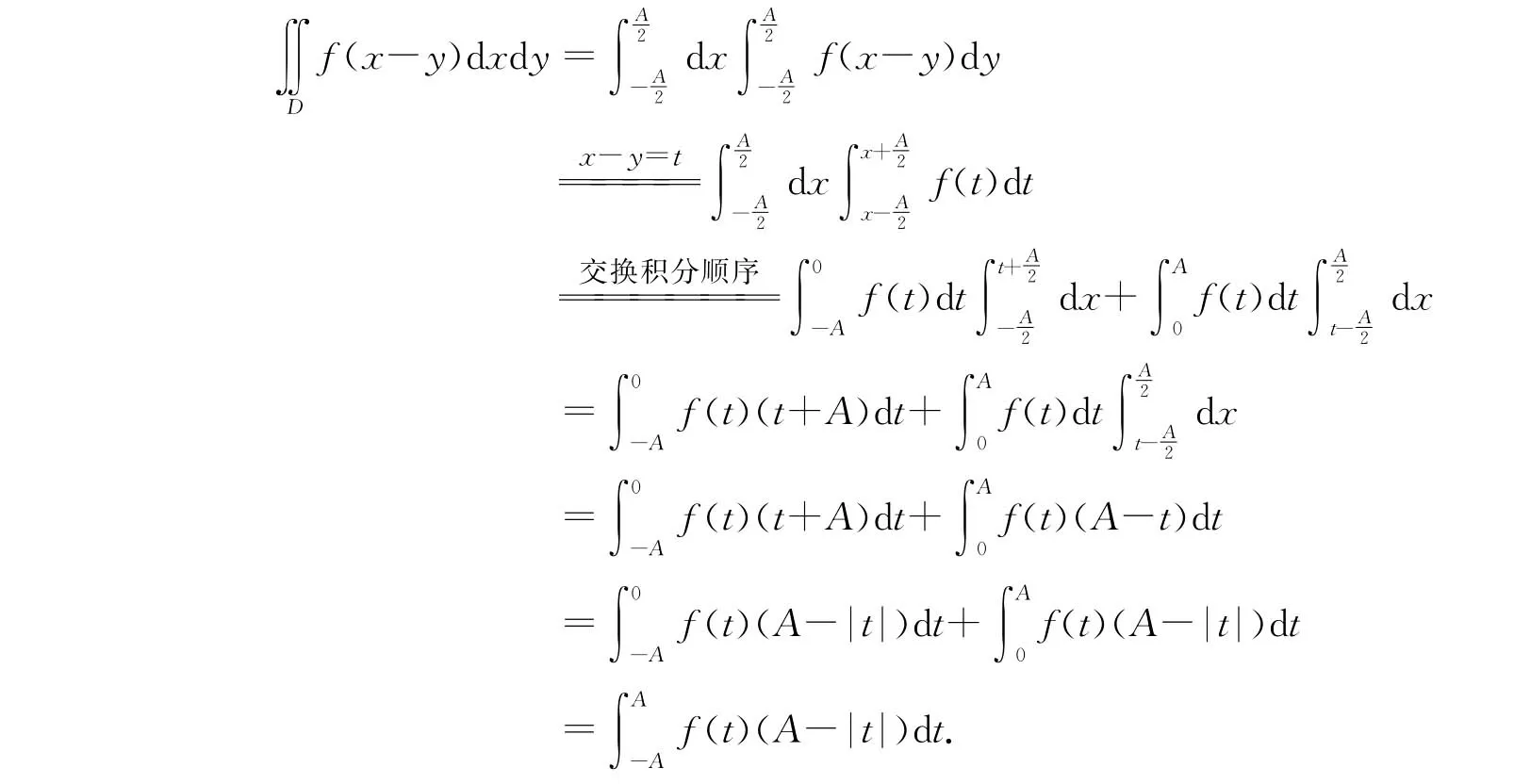
證法2 利用二重積分的變量替換.

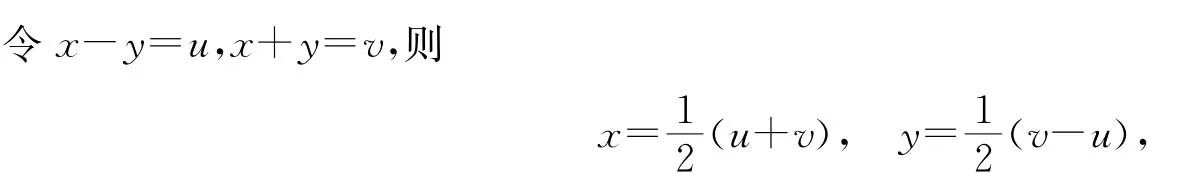
證法3 利用等位線方法（可參閱［1］）.

令x-y＝t，則在D上，-A≤t≤A.

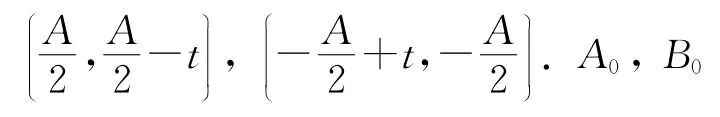
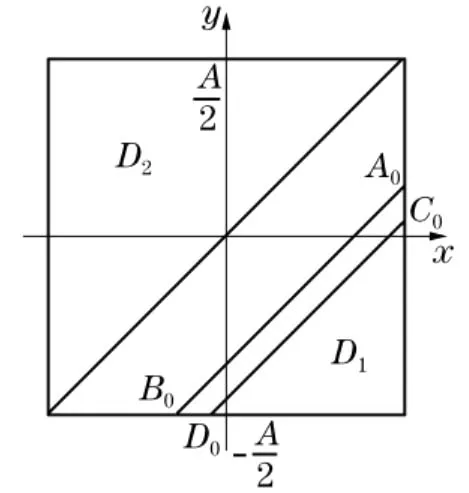
以｜A0B0｜為長為寬的矩形面積作為面積元素d S（t），即

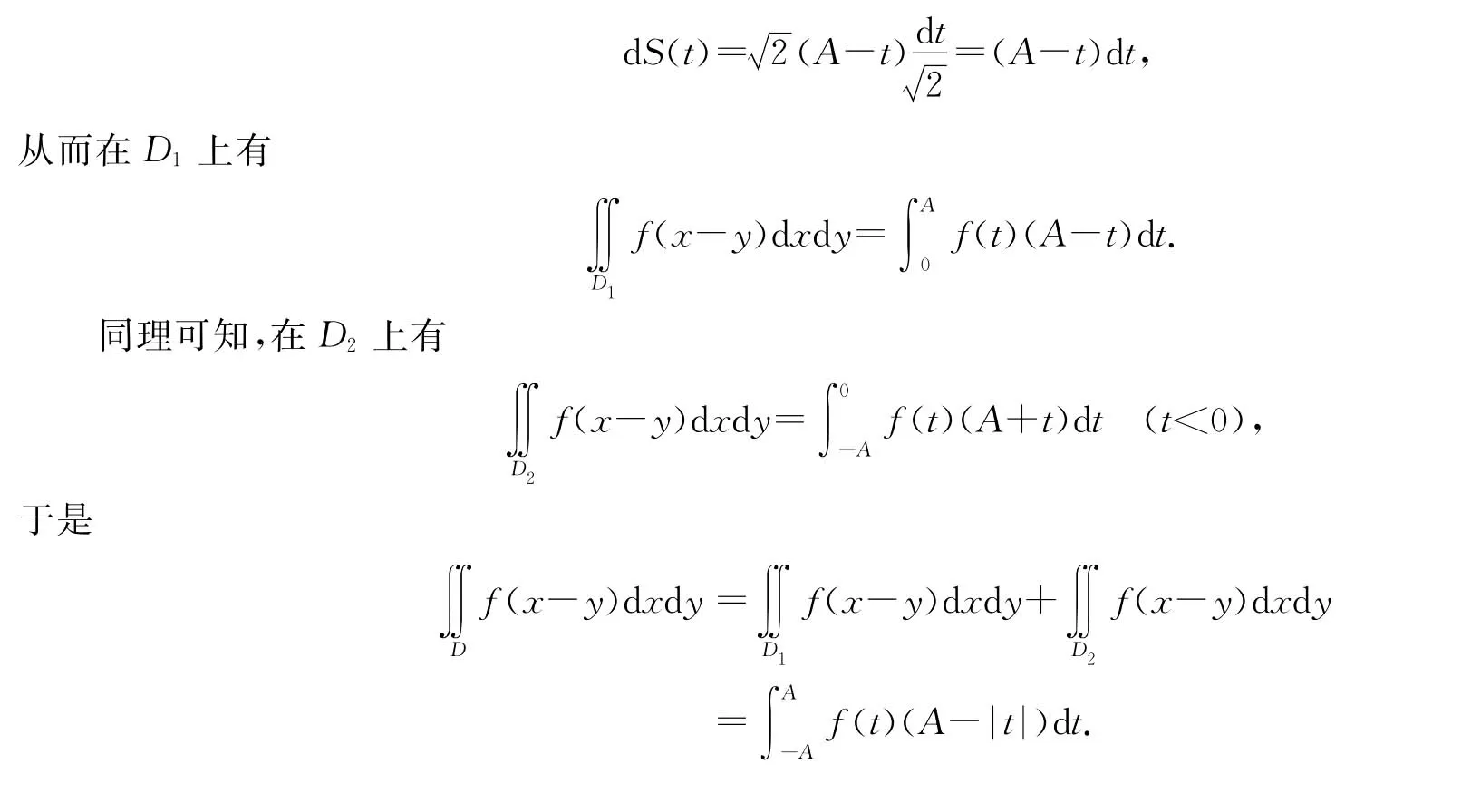
由（1）不難知道，若f（x）為連續的偶函數，則有

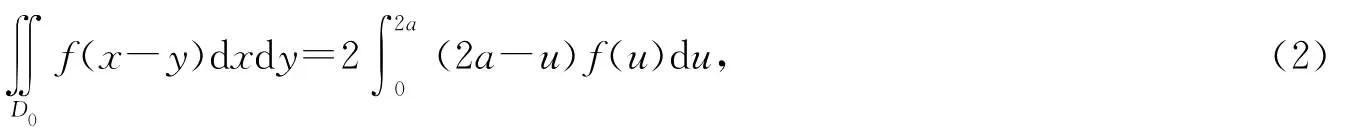
其中a＞0為常數，D0＝｛（x，y）｜x｜≤a，｜y｜≤a｝.（第8屆（1996年）北京市大學生數學競賽題）

利用（1）或（2），不難求解本文開頭的數學競賽題.

在（1）中取f（x-y）＝sin（x-y）2，A＝2，則有

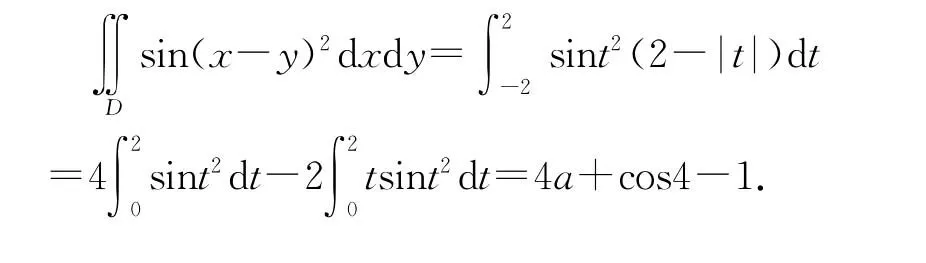
［1］ 黃元兵.等位線（面）的多重積分［J］.高等數學研究，2004，7（2）：28-29.

O172.2

C

1672-1454（2011）04-0156-03

2008-10-20