閉式機架橫梁靜不定力矩的柔性轉(zhuǎn)角計算法

莫軍曉

(中冶陜壓重工設(shè)備有限公司，陜西 西安 710109)

1 前言

用材料力學(xué)方法計算閉式機架橫梁的靜不定力矩時，由于對機架建立的矩形自由框架模型假設(shè)機架橫梁與立柱轉(zhuǎn)角處是剛性的［1-5］，忽略了機架轉(zhuǎn)角處的變形，計算結(jié)果偏離實際情況。

本文提出一種柔性轉(zhuǎn)角計算法。考慮機架橫梁與立柱轉(zhuǎn)角處存在的角變形，并利用該角變形與所受彎矩的關(guān)系，求出橫梁靜不定力矩和角變形的關(guān)系，進而通過卡氏定理求解，得出橫梁靜不定力矩的函數(shù)表達式。

本方法經(jīng)過實例檢驗，計算數(shù)值結(jié)果有足夠高的精度，并且避免了冗長的數(shù)值運算，可以作為建立更復(fù)雜控制模型的基礎(chǔ)工具。

2 柔性轉(zhuǎn)角計算法

計算上橫梁中部的靜不定力矩時，因方法的差別而導(dǎo)致不同的結(jié)果，但是當靜不定力矩數(shù)值求解出來后，其他諸如各個特征點的應(yīng)力、應(yīng)變和位移的計算過程，各種計算方法則大致相同。

本方法認為機架轉(zhuǎn)角處存在附加的、相對的轉(zhuǎn)角變形，并且是可以計算出來的。

轉(zhuǎn)角變形量的大小和立柱上的力矩直接相關(guān)，呈線性正比例關(guān)系。轉(zhuǎn)角變形量由四個部分組成，分別是力矩對上橫梁、立柱上部、立柱下部、下橫梁產(chǎn)生的變形。對應(yīng)的變形值分別用θ1、θ2、θ3和 θ4表示，如圖1 所示。

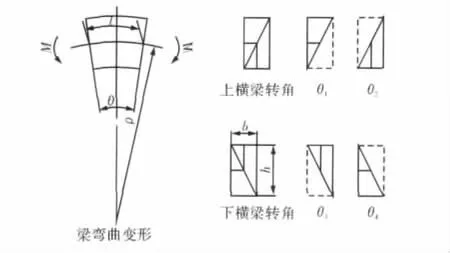
圖1 橫梁與立柱轉(zhuǎn)角處變形分解示意圖

將機架橫梁看作純彎曲梁，受彎后的轉(zhuǎn)角和受彎時的中性層曲率半徑分別用下式計算。

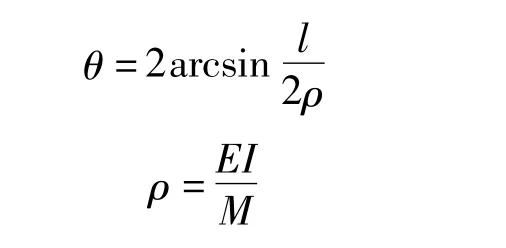
式中，l為彎曲梁長度;θ為彎曲梁受彎后的轉(zhuǎn)角，即角變形量;ρ為彎曲梁中性層曲率半徑;E為材料彈性橫量;I為慣性力矩;M為彎曲梁的彎矩。

上、下橫梁和立柱上、下部都可以看作特殊形式的純彎曲梁，呈倒三角形布置，其彎曲變形是由縱向平行側(cè)面構(gòu)成的長方體純彎曲梁的二分之一，因而轉(zhuǎn)角變形量也相應(yīng)減半。

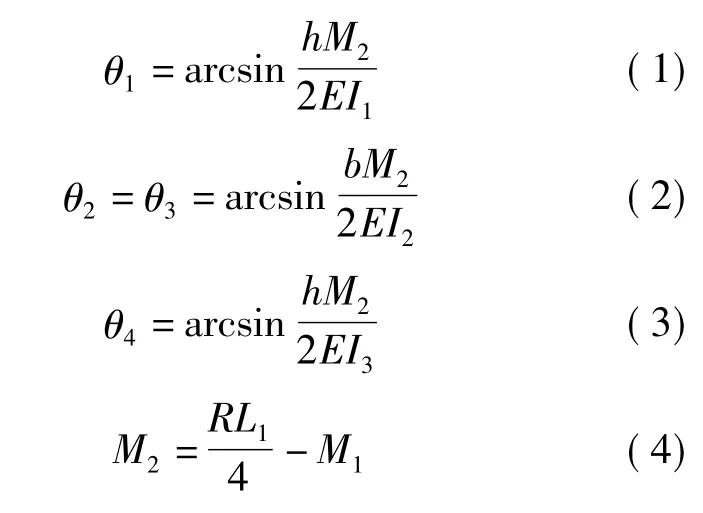
式中，θ1～θ4分別為上橫梁、立柱上部、立柱下部和下橫梁的角變形量;I1～I3分別為上橫梁、立柱和下橫梁的慣性力矩;M1、M2分別為上橫梁和立柱的彎矩;R為軋制力;L1為上、下橫梁中性線長度;b為立柱寬度;h為橫梁高度。

如圖2所示，機架上橫梁中部的轉(zhuǎn)角等于零，利用卡氏原理，求解上橫梁的靜不定力矩M1，然后得出立柱力矩M2。

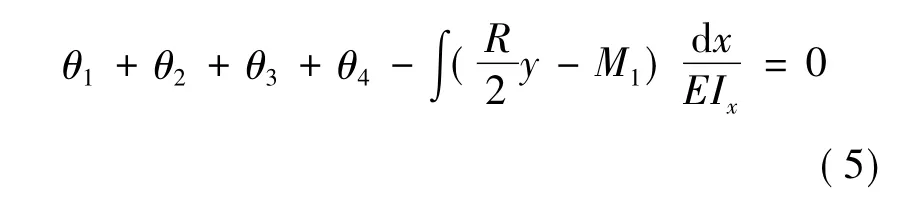
式中，Ix為任意截面的慣性力矩;y為軋制力相對于任意截面的力臂;x為任意截面上機架中性線長度。

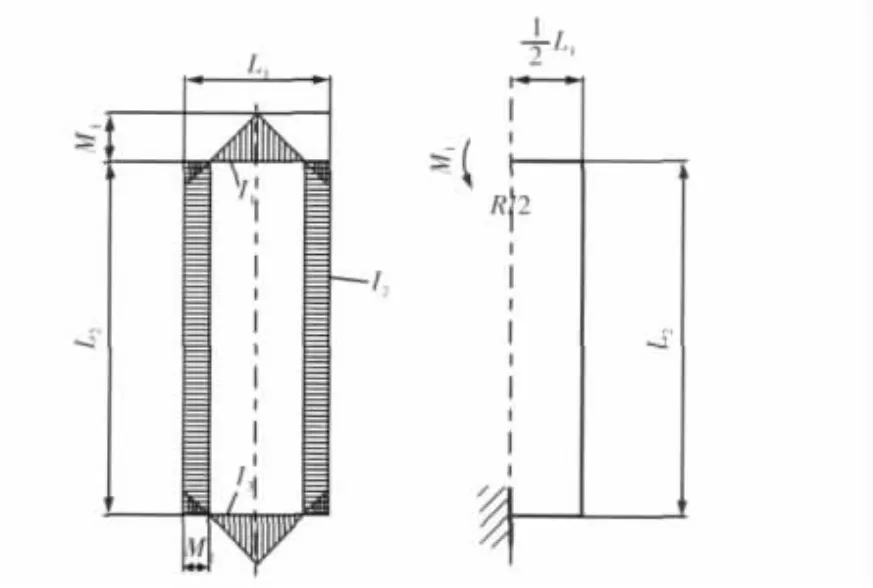
圖2 矩形自由框架彎曲力矩圖

通常取I1=I3，另外運用近似計算arcsinx≈x，式(5)進一步表達為

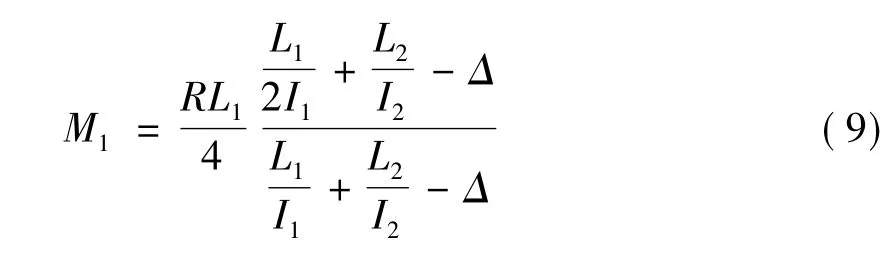
由式(9)知，柔性轉(zhuǎn)角法與材料力學(xué)法的區(qū)別也在于柔性轉(zhuǎn)角法考慮了機架的形狀參數(shù)Δ。

機架計算模型基本尺寸如圖3所示，式(9)可表示為:

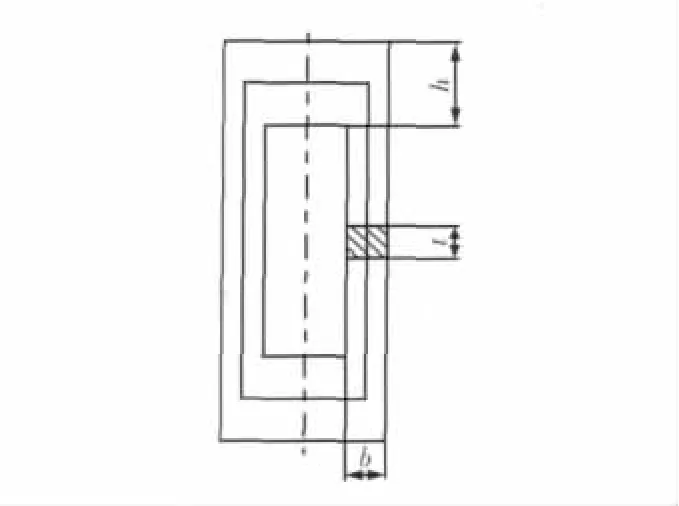
圖3 機架計算模型基本尺寸圖

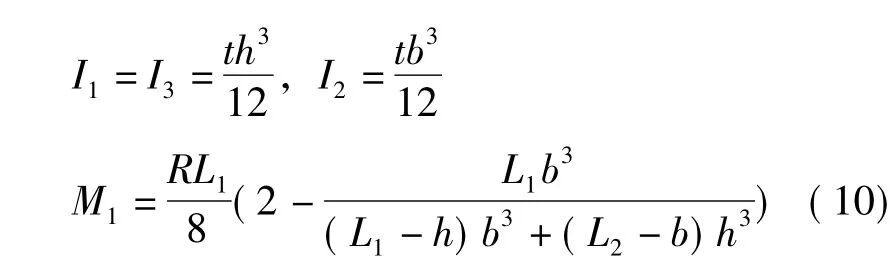
式中，t為機架厚度。

3 計算實例

圖4為某軋鋼廠750 mm四輥冷軋機機架［6］本文分別用材料力學(xué)法、小圓弧法、精確圓弧法、有限元法以和柔性轉(zhuǎn)角法對該機架進行強度計算。計算結(jié)果見表1。

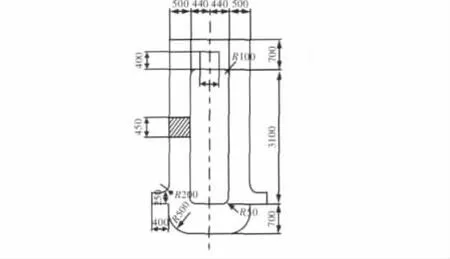
圖4 機架尺寸圖

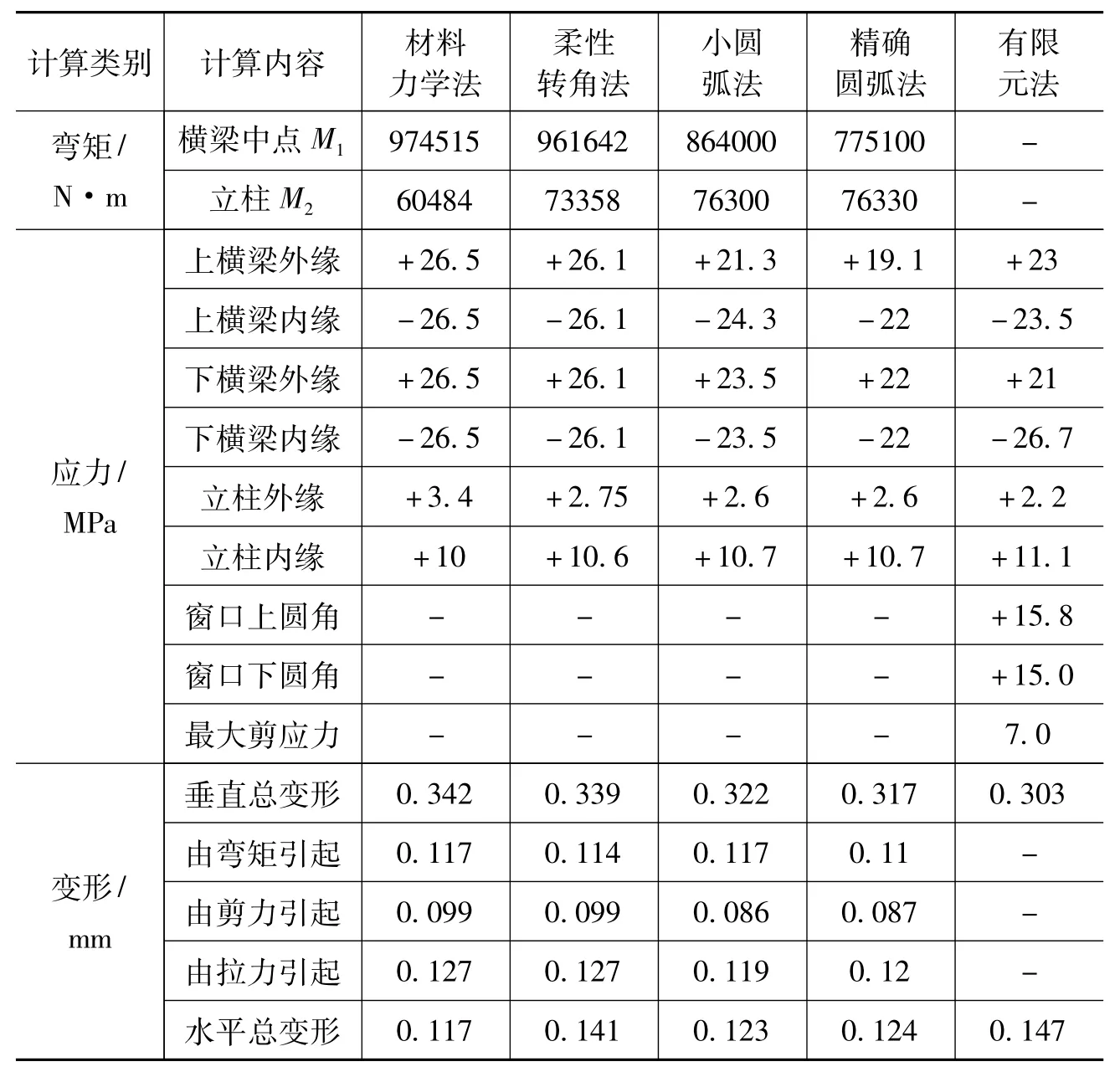
表1 計算結(jié)果

表1中用材料力學(xué)法和柔性轉(zhuǎn)角法計算的M1與M2的總和相同。柔性轉(zhuǎn)角法計算出的M1比材料力學(xué)法小，因而M2能大些。但是M2更接近小圓弧法和精確圓弧法的計算結(jié)果。小圓弧法和精確圓弧法計算的M1與M2要小，導(dǎo)致計算出的橫梁外緣應(yīng)力數(shù)據(jù)偏小。

由于材料力學(xué)法和柔性轉(zhuǎn)角法忽略了上下橫梁的形狀差異，應(yīng)力計算結(jié)果表明上下橫梁內(nèi)外緣應(yīng)力數(shù)據(jù)為對稱分布，與實際情況有較大差別。小圓弧法和精確圓弧法可以如實地反映機架真實的形狀及變化過程，上橫梁內(nèi)外緣應(yīng)力數(shù)據(jù)應(yīng)該和上橫梁內(nèi)外緣應(yīng)力數(shù)據(jù)有所不同，所以計算結(jié)果大部分與有限元法比較接近。

精確圓弧法計算的垂直方向變形最接近有限元法計算結(jié)果，而水平方向變形的計算則以柔性轉(zhuǎn)角法最為準確。

4 結(jié)論

柔性轉(zhuǎn)角法與材料力學(xué)法、小圓弧法和精確圓弧法都是閉式軋機機架的解析算法。材料力學(xué)法算法簡單，計算結(jié)果偏于保守;小圓弧法和精確圓弧法計算過程冗長、模型分段復(fù)雜，計算結(jié)果相對準確;柔性轉(zhuǎn)角法算法比較簡單，計算結(jié)果也比較準確，有一定的參考價值。

［1］ 劉鴻文．材料力學(xué)［M］．北京:高等教育出版社，2004．

［2］ 鄒家祥．軋鋼機械［M］．北京:冶金工業(yè)出版社，2005．

［3］ 喬治．板帶車間機械設(shè)備設(shè)計［M］．北京:冶金工業(yè)出版社，1984．

［4］ 施東成．軋鋼機械設(shè)計方法［M］．北京:冶金工業(yè)出版社，1990．

［5］ 歐光輝．軋機版坊強度與鋼度的精確計算［J］．重型機械，1980，(1)．

［6］ 莫軍曉．750 mm四輥帶鋼冷軋機機架有限元分析［J］．西重科技，1991，(2)．