二階非線性周期邊值問題的正解

胡金燕， 孔令彬

( 東北石油大學 數學科學與技術學院，黑龍江 大慶 163318 )

0 引言

研究二階非線性周期邊值問題，即

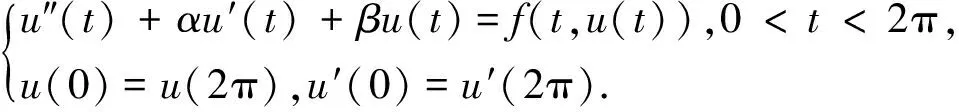
(1)

式中：參數α>0,0<4β-α2<1.

二階非線性周期邊值問題出現在物理及應用數學領域中[1-8]，人們對此進行研究，討論含單參數的二階非線性周期邊值問題，獲得正解存在性結果[1].有關含雙參數二階非線性周期邊值問題的研究結果還不多見.筆者研究一類二階非線性周期邊值問題式(1)(簡稱問題(1))，在非線性項滿足適當的條件下，證明正解的存在性.

1 問題假設

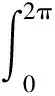
定義：稱u(t)為邊值問題(1)的1個正解，如果它滿足

(ⅰ)u(t)∈C2(0,2π)∩C1[0,2π],u(t)>0,t∈(0,2π)；

(ⅱ)u″(t)+αu′(t)+βu(t)=f(t,u(t)),并且u(t)滿足

u(i)(0)=u(i)(2π),i=0,1,

則主要結果是

定理1假設(H1)，(H2)或(H1)，(H3)成立，則邊值問題(1)至少存在1個正解.

推論假設(H1)及條件之一成立：

則邊值問題(1)至少存在1個正解.

為證明定理1，需要用到引理.

引理1[9]設E是Banach空間，K是E中的錐，T:K→K是全連續算子.

(1)如果對任何u∈?Kr及任何0<λ≤1都有λTu≠u，則i(T,Kr,K)=1；

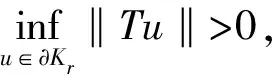
2 問題(1)的等價形式與Green函數估計

引理2[1]若線性周期邊值問題

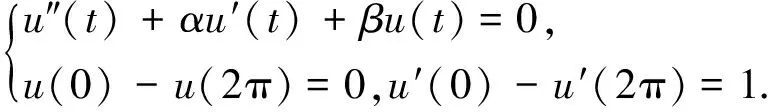
(2)

有唯一解r(t)∈C2[0,2π]，則周期邊值問題：

有唯一解，即

其中

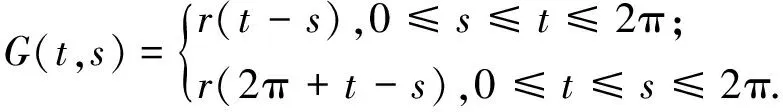
引理3線性周期邊值問題式(2)存在唯一解

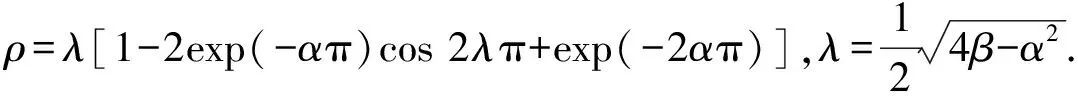
證明：注意到α>0,0<4β-α2<1，直接計算即可.

由r(t)的表達式，容易知道r(t)>0,t∈(0,2π).再根據引理2和引理3可知，問題(1)等價于積分方程：

(3)

其中

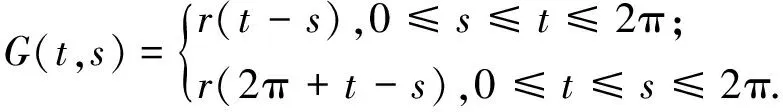
引理4?s,t∈[0,2π]，成立不等式：

證明設h(t)=sinλt+exp(-απ)sinλ(2π-t),t∈[0,2π]，則h(0)=e-απsin 2λπ，h(2π)=sin 2λπ，t∈[0,2π]并且

h′(t)=λcosλt-λexp(-απ)cosλ(2π-t),

h″(t)=-λ2[sinλt+exp(-απ)sinλ(2π-t)]<0,

故h(t)于[0,2π]是凸函數.令h′(t)=0，可得

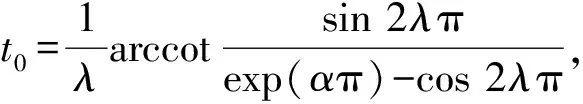
h(t0)=sinλt0+exp(-απ)sinλ(2π-t0)=

從而

h(t)≤max{h(0),h(2π),h(t0)}≤

max{exp(-απ)sin 2λπ,sin 2λπ,exp(-απ)+1}≤

1+exp(-απ).

另外

h(t)≥min{h(0),h(2π),h(t0)}≥

min{exp(-απ)sin 2λπ,sin 2λπ,1-exp(-απ)cos 2λπ}≥

exp(-απ)[1-exp(-απ)cos 2λπ]sin 2λπ.

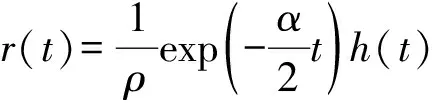
因此對?s,t∈[0,2π]有

3 定理1的證明

定義映射：Φ:C[0,2π]→C[0,2π]，

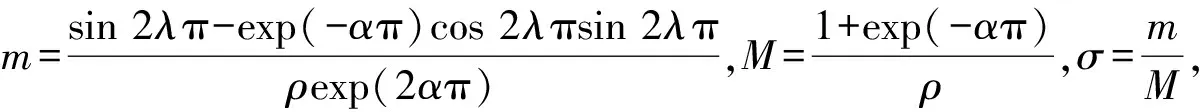
在C[0,2π]中定義錐K：

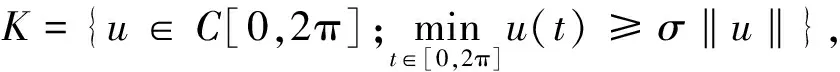
于是?u∈K，由引理4知

故Φ(K)?K.另外，容易證明Φ:K→K全連續.

現在證明定理1.

情形1：由(H2)可知，可選擇ε∈(0,β)及r>0使

f(t,u)≤(β-ε)u,0≤u≤r,?t∈[0,2π].

證明?u∈?Kr及0<μ≤1有μΦu≠u.若不然，則存在u0∈?Kr,0≤μ0≤1使μ0Φu0=u0，由映射Φ的定義知u0(t)滿足

(4)

將式(4)的方程兩邊從0到2π積分并利用條件得

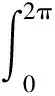
由引理1知i(Φ,Kr,K)=1.

再由(H2)可知，存在ε>0及H>0使

f(t,u)≥(β+ε)u,u≥H,?t∈[0,2π].

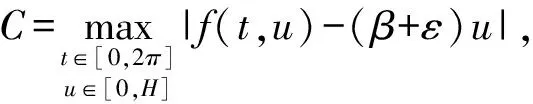
f(t,u)≥(β+ε)u-C,u≥0.

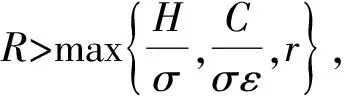
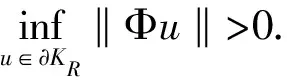
證明?u∈?KR及μ≥1有μΦu≠u.若不然，則存在u0∈?KR,μ0≥1使μ0Φu0=u0，于是式(4)成立，對式(4)兩邊從0到2π積分得

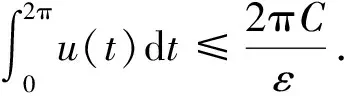
由引理1知i(Φ,KR,K)=0.再根據不動點指數的可加性知

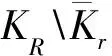
情形2：由(H3)可知，存在ε>0和r>0使

f(t,u)≥(β+ε)u,0≤u≤r,?t∈[0,2π].

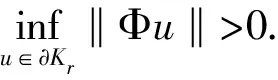
證明?u∈?Kr及μ≥1，有μΦu≠u.若不然，則存在u0∈?Kr,μ0≥1使μ0Φu0=u0，于是u0(t)滿足式(4).將式(4)從0到2π積分得

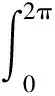
再由(H3)可知，存在ε∈(0,β)及H>0使

f(t,u)≤(β-ε)u,u≥H,?t∈[0,2π].

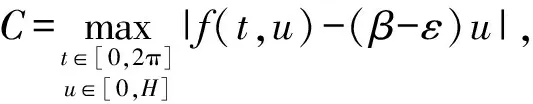
f(t,u)≤(β-ε)u+C,u≥0,?t∈[0,2π].

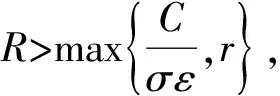
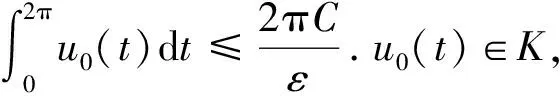
由不動點指數的可加性知

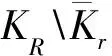
4 結束語

研究一類含雙參數二階非線性周期邊值問題，在非線性項滿足適當的條件下，利用對格林函數的估計不等式和錐不動點定理，給出了問題正解存在的充分條件,證明了其正解的存在性.