意象圖式理論視角下的英漢數字隱喻

吳海英(天津工業大學 外國語學院，天津 300160)

意象圖式理論視角下的英漢數字隱喻

吳海英
(天津工業大學 外國語學院，天津 300160)

數字作為一種特殊的語言，除本身的計算意義外，還具有文化內涵。這種現象是用數字來理解和體驗其他領域的種種觀念，是聯想、類比的結果，帶有顯著的隱喻性質。意象圖式理論可用來探析英漢數字隱喻共性的認知理據，如部分-整體圖式用以解釋完美是數、整體是數，起點-路徑-目標圖式用以解釋線性數量關系。意象圖式對數字隱喻具有一定的解釋力。

數字；隱喻；意象圖式

一、引 言

數字是一種特殊的語言，赫弗德(J. R. Hurford)在其《語言與數字》一書中說：“一般說來，數字明顯是種神秘的、不規則的語言，因為它們所表示的那些數目，并不像其他語言表示人、位置、事物、行為、狀況和性質這樣實際存在的東西。”然而，“……數字系統以清晰的方式與語言充分融合在一起，并植根于其中。”[1]更進一步講，數字系統是充分地與它們植根于其中的文化融合在一起的。因而，除計數意義外，這些數字還具有種種象征意義。英語和漢語中均有此類現象。例如：

(1)亦余心之所善兮,雖九死其猶未悔。(屈原《離騷》)(極限)

(2)白發三千丈,緣愁似個長。(李白《秋浦歌》)(多，虛數)

(3)Every time she wins a match she'sin seventh heaven!(每次贏了比賽，她都快樂無比。)(極為快樂)

(4)A man passed down the street, which werethree sheets in the wind.(一個醉漢沿街而下，搖搖晃晃，步履蹣跚。)(醉酒后東倒西歪)

這些象征意義在中西方的哲學、宗教、神話、巫術、詩歌、習俗中不斷出現，并具有頑強持久的傳承力量，世代相沿。它已經根植于各自民族的心靈深處，作為一種審美化的集體無意識，在潛移默化中建構著人們日常的話語世界。從本質上講，這種現象是用數字來理解和體驗其他領域的種種觀念，是聯想、類比的結果，帶有顯著的隱喻性質。

據對英漢語料的考察，英漢基本數字隱喻意義比較如表1所示。

表1 英漢基本數字隱喻意義比較

上述英漢數字隱喻意義存在諸多共性，有些驚人地相似，如“1”都有哲學意義上的“本原”“統一”之意象，“2”表“對立”，“3、5、9”表“吉祥”等。這些英漢數字的隱喻意義均來自數范疇的數字本體特征，并具哲學意義。這些數字兼具神秘性和模式化的特點。

那么，這些共性的背后的認知理據是什么呢？認知語言學對人類認知研究的共性取向為找尋英漢數字隱喻共性幕后的工作機制提供了可能性。學界對于數字隱喻的專門探討還不多見，本文試從認知語言學視角分析數字隱喻心理表征的形成機制。所有未標出處的漢語語料均來自廈門大學語言技術中心開發的中文自然語料文本語料庫，英語語料來自英國國家語料庫。

二、意象圖式對英漢數字隱喻的解釋

意象圖式是認知語言學為描寫語義結構而提出的假設。約翰遜和萊考夫認為意象圖式是建立在身體經驗基礎上所形成的基本認知結構，對于意象圖式的理解側重于身體與外部世界環境的互動關系。為了適應環境，并且認識和把握客觀世界，人們的感覺和知覺、行為會建立起一定的模式。這些反復出現的模式、程式就形成了意象圖式的基礎。[2]其中，身體的空間運動模式、操縱物體的經驗等感知模式是最基本的意象圖式。由于意象圖式的體驗性和邏輯性，某些意象圖式可作為解釋英漢數字隱喻工作機制的分析工具。

萊考夫在《女人、火和危險事物：范疇揭示了什么奧秘》中從認知的角度論述了數學，認為數學是一種認知活動，高度形式化的數學產生于人類的各種經驗，如計算、測量、證明、問題解決、分組等。這些人類活動都有一個一般的圖式結構。[3]362那么，與數學相關的概念都有其對應的意象圖式。例如：實體性——ENTITY(實體圖式)；對應性——LINK(連接圖式)；連續性——PATH(OF MOTION)(路徑圖式，移動)；順序性——DIRECTION(方向)；因素(或分解)——PART-WHOLE, SEPARATION(部分-整體，分離圖式)；數量相等——BALANCE(平衡圖式)；分類——CONTAINER(容器圖式)。

這些數學概念(術語)來自許多人長期仔細的觀察和體悟，對一種平常的現象得出一致的理解，然后將其轉化成數學術語。數學是產生于人類日常經驗的結構，是一種純形式，它又用來理解其他經驗。[3]364那么，意象圖式就是數字隱喻的工作機制。但是，萊考夫并未列舉具體語言實例來說明。本文將以PART-WHOLE(部分-整體圖式)、BALANCE(平衡圖式)及SOURCE-PATH-GOAL(起點-路徑-目標圖式)3種意象圖式為例，來解釋英漢數字隱喻的工作機制。

1.“完美是數，整體是數，極限是數”與部分-整體圖式

部分-整體圖式來源于身體經驗。人體是一個由部分構成的整體。健康的人都能意識到自己身體的完整性及身體各部分構件的狀況，并能操縱這些部件。其生理基礎為：人本身以及其他物體是由部分組成的整體。其構成要素為：整體、部分、構造。基本邏輯是：此圖式是不對稱的，如果A是B的部分，那么B就不是A的部分，它是不自反的。如“蘋果在樹上”成立，而“樹在蘋果上”就不合邏輯；“汽車缺少配件”成立，“零件缺少汽車”就不成立。而且不存在有整體無部分的情況，但是即便所有的部分都存在，也不意味著就構成了整體。如即便是所有汽車零件都在，也不一定是一個完整的汽車。只有部分存在，整體才存在，照這樣推理，如果部分遭到破壞，整體也會被破壞。

這一圖式可以解釋英漢中都存在的滿數，如3、4、6、9、10。如“10”表示完滿、完美，是因為“10”被看做一個整體，它包括所有部分之和，是完整無缺的。有整體存在就有部分存在，所以，“10”表示“完整”的同時，也暗含著事物本身有一個既定結構，有“部分”和“不完整”。再如“1”隱喻為“統一”，是因為“1”是一個整體，把所有部分歸為一個整體即為“統一”。另外，“極限”的概念也可從部分和整體的關系中得出。又因部分和整體可以分離，所以可解釋“2”的對立性和“分離”隱喻。例如：

(1)行兵之道，天地之寶，九天九地，各有表里。九天之上，六甲子也，九地之下，六癸酉也。子能順之，方可保全。(《后漢書·皇甫嵩傳》)(極限)

(2)另一主持阮子健即說：“三姑的節目是一張嘴巴、兩件蛋散(香港俚語，指沒用的人)、四面受敵，但八面威風。”(全部，整體)

(3)如果你選擇了這一條路，那就平心靜氣地走下去，因為三心二意是無法成就一個過程的，當回頭整理自己走過的路的時候，也會發現那是一段凌亂且不完整的歲月。(另外，不同)

(4)His wife knew that he wastwo-timingher but she didn’t say a thing. (妻子雖然知道有外遇，卻忍氣吞聲。)(分離，另外)

(5)The good book, if we are to believe it, says we are entitled tothree score years and ten. (如果我們相信的話，圣經上說，我們都有資格活到70歲。)(極限)

(6)During the war my family was scattered to thefourwinds. (戰爭年間，我們一家人被迫流落四方。)(全部，處處)

2.“相同，一樣”與平衡圖式

平衡圖式的生理基礎是：平衡就是物體的對稱性，如形狀、大小、位置等；人身體的器官是對稱的、平衡的。其構成要素是：支點和杠桿的兩邊。基本邏輯為：(1)對稱性。A和B平衡，那么B和A也平衡。(2)等價關系的傳遞性。如果A和B平衡，且B和C平衡，那么，A和C也平衡。它們之間的等價關系以支點為中心傳遞。(3)自反性。A和A本身平衡。如圖1所示。

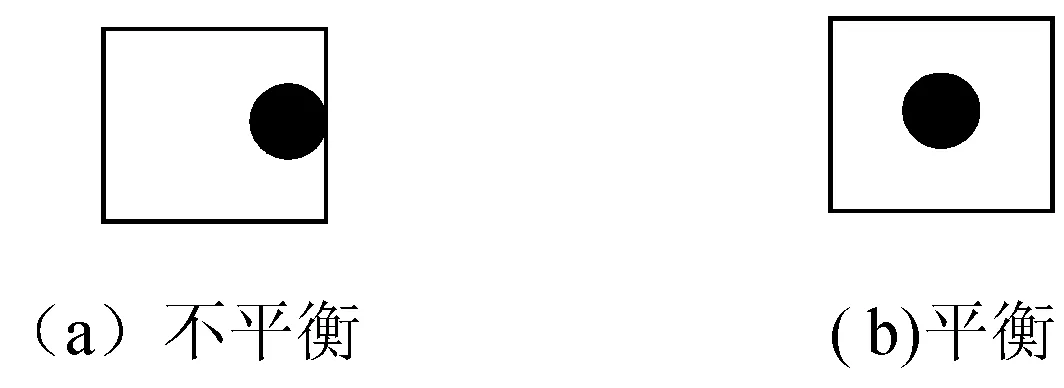
圖1 平衡圖式

數量的相等來自于人類的平衡經驗，如周圍物體的對稱性(山體、樹葉)。人體可以站立、行走，而嬰兒從會爬到搖搖晃晃地站立，有時會跌倒在地，他爬起來再走，再跌，再試，直到新的世界展現在他們的面前——平衡的直立的世界。人的身體器官也是一個動態平衡的系統。可以從身體失去平衡的角度理解平衡，如吃得過飽、手腳太冷、口太干等，都是整個身體系統失去了生理平衡造成的。無論物體還是人體的平衡，都體現了一種重量和力的平衡性，平衡和失衡是重量和力量的平衡和失衡。日常生活中的平衡經驗映射到數學領域，數量相等被看做是一種平衡，支點兩邊數量等同。如果左手里拿2 kg的蘋果，那么為保持平衡，右手也必須有2 kg的蘋果(或其他東西)。這邊添加1 kg，那邊也得添加1 kg，才能繼續保持平衡。物體映射到數量(實體)，物體的重量映射數量的價值，重量多余的一邊映射數量上的多余，杠桿的支點就是等式的等號。

英漢中的數字“1”有“相同，一樣”的隱喻意義，可以通過平衡圖式解釋為數量相等或價值相當。上文所列實例均可以以此來解釋，又如：

(1)剛要尋別的妹妹去，忽見前面一雙玉色蝴蝶，大如團扇，一上一下迎風翩千，十分有趣。(《紅樓夢》)

(2)鵬振嘆了口氣道：“十年河東，十年河西，哪個保管得了那些？我這事就托重你了。”(張恨水《金粉世家》)

(3)Oneand the same idea occurred to each of them.(他們都產生同樣的想法。)

(4)The apples weigh six jin. Let's take themfifty-fifty.(這些蘋果有6斤重，我們對半分吧。)

上例中的“一”和“one”已失去其純數字意義，引申出“相同，相等”之意。由于數量或價值相同，因此是平衡的、對稱的。兩個漢語數字熟語的隱喻意也反映出數量上的相等，支點兩邊分別是“一上”和“一下”、“十年河東”和“十年河西”，兩邊的數量完全相同，顯示出兩種實體的對稱性。“一上一下”意思是上下交替跳動，“十年河東，十年河西”指世事盛衰會發生輪轉變化，也指矛盾的兩方面互相轉化。從這里可以看出支點兩邊等價關系的傳遞性。“one to one”(平局)、“fifty-fifty”(一半一半，平分)、“six of one and half a dozen”(一個半斤，一個八兩，重量相等)都表達了相等的數量關系，它們的含義中都有平衡對稱的因素。漢語中還有很多類似的數字熟語，例如：一個半斤，一個八兩；一唱一和；天無二日，人無二理；三起三落；六言六弊；七擒七縱；八遇八克；九轉九還等。

再看數量不等是失衡的例子：

(5)聽見寶釵自己推讓，他心里本早打算過寶釵生日，因家中鬧得七顛八倒，也不敢在賈母處提起。(《紅樓夢》)(動作行為的不平衡性)

(6)If I was to go from home, everything would soon go tosixes and seven. (假如我離開家，家里馬上就會一團糟。)(“sixes”和“seven”之間不平衡)

以上句子中含有兩個不同數字之間的搭配，它們之間的數量關系不相等，一方多于另一方，表達了動作行為的不平衡性，含義為多、亂。在漢語中，模式為“七…八…”的熟語很多含貶義，意為“多、亂”，如亂七八糟、七上八下、七嘴八舌、七折八扣、七拼八湊、七狼八狽、烏七八糟、雜七雜八等。平衡圖式的支點兩邊分別為兩個實體“七”和“八”，它們的數量不相等，即價值不同，平衡被打破，處于一種失衡的狀態。而人們日常經驗中的平衡狀態(物體、人體的平衡性)被普遍認為是健康的、審美的、舒適的，所以這種失衡狀態被認為是非正常狀態，它是非審美的、不舒適的。另外還有其他類似的數字組合用法，有的雖然不含貶義，但也可以用數量失衡來解釋不同實體之間的價值差異。從以下的熟語中可以看出兩邊數量的差異和失衡的程度：一舉兩得；一問三不知；一日三秋；丟三落四；三寸鳥，七寸嘴；三分吃藥，七分調理；一步九回。

3.數量關系和線性數量規模與起點-路徑-目標圖式

該圖式的生理基礎為：當物體從一個地點移到另一個地點時，一定有起點、終點和路徑。其構成要素為：起點、終點、路徑、方向。如圖2所示。

圖2 起點-路徑-終點圖式

線性數量規模可以理解為線性順序圖式(LINEAR-SCALE)。線性規模就是路徑，線性順序是起點、終點，它是單向疊加的，有方向性。例如：

(1)金黃的丁香花在崖壁中如瀑布般垂下，點綴著一望無際的原野。(方向性)

(2)飛流直下三千尺，疑是銀河落九天。(終點，極限)

(3)He’s now the boss’s numbertwoand travels with him wherever he goes.(身為老板的左右手，他與老板現在是形影不離。)(順序)

(4)The whole family weredressed (up) to thenineswhen they left for the wedding.(全家人穿戴一新，前去參加婚禮。)(線性終點，極限)

以上例子中的數字分別表達了不同事物的線性規模，不同個體在空間和時間上的位置、移動方向、移動距離等，可在一定程度上解釋某些數字隱喻，如初始、極限、比較等。

三、結 語

從以上分析中可以看出，某些意象圖式可以用來解釋英漢隱喻現象中所表達的部分-整體性、平衡性和線性數量關系等，從更深層面挖掘了英漢數字隱喻的認知理據，有益于進一步探究數字隱喻心理表征的形成機制。

[1]HURFORD J R. Language and number: the emergence of a cognitive system[M]. Oxford: Basil Blackwell, 1987: 5.

[2]JOHNSON M. The body in the mind: the bodily basis of meaning, imagination, and reason[M]. Chicago: The University of Chicago Press, 1987: 97-101.

[3]LAKOFF G. Women, fire, and dangerous things[M]. Chicago: The University of Chicago Press, 1987.

EnglishandChinesenumeralmetaphorundertheoryofimageschema

WU Hai-ying

(School of Foreign Languages, Tianjin Polytechnic Univ., Tianjin 300160, China)

Numeral is a special part of language which not only processes the meaning of counting, but also has cultural implications. It is the result of associations and analogy, the understanding of various ideas of other fields through numerals. It obviously has the nature of metaphor. The theory of image schema can be applied to analyze the cognitive motivations of English and Chinese numeral metaphor. The completeness and perfection of numerals can be explained by PART-WHOLE schema; similarly, the linear relations of numerals can be explained by SOURCE-PATH-GOAL schema. Therefore, image schema theory can be applied to explain numeral metaphor.

numeral; metaphor; image schemA

H0

A*

1671-7041(2011)01-0116-04

2010-10-07

吳海英(1968-)，女，山東菏澤人，博士，副教授；E-mailjerrywhy@126.com