地方高校科技創(chuàng)新效率評價研究
——基于超效率的三階段DEA分析

李 瑛，崔宇威

（1.南開大學周恩來政府管理學院，天津300071；2.天津氣象局科技處，天津300074）

地方高校科技創(chuàng)新效率評價研究
——基于超效率的三階段DEA分析

李 瑛1，崔宇威2

（1.南開大學周恩來政府管理學院，天津300071；2.天津氣象局科技處，天津300074）

筆者采用2007年中國地方高校科技數(shù)據(jù)，首先對人力投入進行因子分析，提取三個公因子，在此基礎(chǔ)上運用超效率的三階段DEA對28個省市的地方高校的科技創(chuàng)新效率進行了評價分析，并對效率的影響因素進行了分析，實證結(jié)果表明：在所采用的效率評價體系下，地區(qū)的經(jīng)濟發(fā)展水平和文化水平以及政府撥款在科研經(jīng)費中所占的比例對效率沒有影響，但對于某些地區(qū)，在投入不變的條件下，地方高校中的研發(fā)機構(gòu)數(shù)太少和研究項目數(shù)太多是制約效率提升的主要因素。

地方高校；科技創(chuàng)新效率；因子分析；三階段DEA；SDEA

高校具有豐富的科技人力資源和充足的研發(fā)機構(gòu)以及大量的研發(fā)項目，是區(qū)域和國家創(chuàng)新系統(tǒng)的重要組成部分，對地方高校創(chuàng)新效率及其影響因素的研究可以為地方政府及有關(guān)部門制定相關(guān)科技政策，為高等教育的改革與發(fā)展，提供理論指導和政策依據(jù)。

目前學術(shù)界對高校科技創(chuàng)新體系的評價研究較少，這些研究主要分為兩部分：一部分是對創(chuàng)新能力的評價，如梅軼群［1］、梁燕等［2］對擬定的評價指標體系賦權(quán)，在此基礎(chǔ)上對高校的科技創(chuàng)新能力進行綜合評價；王光平［3］在擬定的評價指標體系的基礎(chǔ)上用因子分析對全國30個省市的高校的科技創(chuàng)新能力進行了評價。另一部分是周靜［4］110－117、張海燕［5］等運用單階段DEA對不同地區(qū)的高校的創(chuàng)新效率進行研究，在這些DEA評價模型中指標之間往往出現(xiàn)交叉（如“支出經(jīng)費總額”和“業(yè)務(wù)費”），有研究表明［6］，指標之間的這種交叉會對DEA的評價結(jié)果產(chǎn)生影響；同時，單階段的DEA模型給出的效率沒有將環(huán)境及隨機因素對效率的影響剝離。因此，本文首先對相互交叉又不能相互替代的投入指標進行因子分析，用提取的公共因子替代原始投入指標，進行三階段DEA分析。

一、模型與方法

數(shù)據(jù)包絡(luò)分析（DEA）運用線性規(guī)劃求解效率前沿面，對于多輸入和多輸出的效率評價尤為適用，因為它不用事先對函數(shù)和分布的形式進行假設(shè)，也不用對多輸入和多輸出進行賦權(quán)，減少了主觀判斷對評價的影響。最常用的模型是Charnes，Cooper和Rhodes在1978年提出的CCR（規(guī)模報酬不變）和Banker，Charnes和Cooper在1984提出的BCC（可變規(guī)模報酬），這二者的結(jié)合可以獲得評價單元的純技術(shù)效率和規(guī)模效率。關(guān)于DEA的研究與應用較為成熟，對于原理本文不再贅述。

單階段的DEA給出的效率測量不僅僅是管理的有效性，它包括了環(huán)境和隨機因素對效率的影響，為了解決這一問題，研究者們提出了三階段DEA模型，目前國內(nèi)外學術(shù)界在研究時使用的三階段DEA模型有兩種。一是Fried et al.于2002年提出了三階段DEA模型［7］：第一階段：傳統(tǒng)的DEA模型（BBC模型），用以計算輸入和輸出的松弛變量；第二階段：構(gòu)建相似SFA模型，以松弛變量作因變量，環(huán)境變量作自變量進行分析，依據(jù)分析結(jié)果對投入或輸出進行調(diào)整；第三階段：用調(diào)整后的輸入或輸出重新進行DEA分析。當分析的決策單元的數(shù)量較少時，松弛變量只有幾個非零值，會使SFA的分析結(jié)果失真。另一個是Michael F.Gormana和John Ruggiero［8］，在2008年對美國49個州的警察部門的績效評價時用到的三階段DEA，該方法最早由John Ruggiero在1998年提出，它的模型構(gòu)建和運用分三個階段：第一階段，傳統(tǒng)的單階段DEA分析，借此計算每個決策單元的效率；第二階段，進行Tobit分析，以第一階段的效率值為因變量，環(huán)境變量作自變量，依據(jù)分析結(jié)果計算每個決策單元的環(huán)境指數(shù)；第三階段，將環(huán)境指數(shù)作為投入，重新計算各個決策單元的效率。該模型在國內(nèi)的應用尚未見報道。本文在該模型的基礎(chǔ)上采用超效率DEA分析，同F(xiàn)ried et al.的模型相似，該模型在第二階段的回歸中用的因變量是第一階段計算的效率值，而DEA有效單元的效率值都為1，這同樣會使回歸結(jié)果失真。

（一）第一階段超效率DEA模型

第一階段的目的是計算沒有考慮環(huán)境因素時各個地區(qū)的效率，傳統(tǒng)的DEA分析對于有效的決策單元的效率未加區(qū)分（給定效率值），在該階段與John Ruggiero不同的是我們采用SDEA（超效率數(shù)據(jù)包絡(luò)分析）計算效率值。SDEA最早由Per Andersen和其同事Niels Christian Petersen在1993年提出，該模型能夠?qū)EA有效的單元進行排序，其基本思想是在進行某個決策單元效率評價時，用其他所有決策單元的投入和產(chǎn)出的線性組合替代該決策單元的投入和產(chǎn)出，它自身被排除在外。一個DEA有效的決策單元在效率值保持不變的條件下其投入按比例的增加，其投入增加比例即其超效率評價值。

該階段的分析中給出的效率反應的是由管理、環(huán)境和隨機因素三者決定，它沒有說明地方高校科技創(chuàng)新的低效率是管理不善造成的，還是環(huán)境不利或其他隨機因素造成的。

（二）第二階段回歸分析

在第一階段SDEA分析中給出的效率值不再是介于0和1之間，因此我們用O.L.S.回歸將環(huán)境因素對效率的影響量化，假若有m個環(huán)境變量，n個地區(qū)，則效率與環(huán)境變量的回歸模型如下：

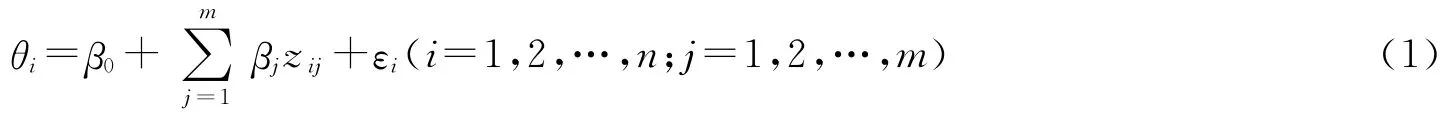
其中θi是第i個評價地區(qū)高校的第一階段創(chuàng)新效率值，βj是環(huán)境因素zj的回歸系數(shù)，是環(huán)境因素對第i個地區(qū)高校創(chuàng)新效率的影響。

（三）第三階段調(diào)整投入后的DEA分析

依據(jù)環(huán)境變量的值我們可以得到每個地區(qū)環(huán)境變量對效率影響的預測值，定義該值為環(huán)境指數(shù)，它由下式給出

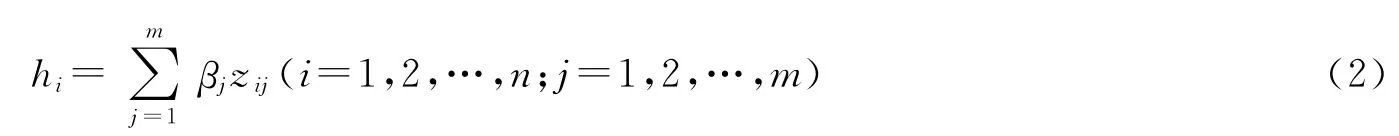
具有最大環(huán)境指數(shù)值的地區(qū)，高校所面臨的科技環(huán)境是最有利的。因此，在第三階段的分析中將該指數(shù)作為輸入之一，重新進行DEA分析，所得到的效率值消除了環(huán)境對效率的影響。因為，就科技環(huán)境而言，各個地區(qū)的高校處在同一起跑線上。

二、數(shù)據(jù)與指標

因為投入和產(chǎn)出指標的選取會直接影響到評價結(jié)果。因此，在指標選取時一定要符合完備性，不能遺漏重要的評價指標，同時，還要考慮指標之間的相互獨立，因為指標之間的重復同樣會影響評價結(jié)果。本文在對相關(guān)文獻分析的基礎(chǔ)上，依據(jù)高校科技創(chuàng)新的內(nèi)涵和結(jié)構(gòu)以及高校科技創(chuàng)新體系數(shù)據(jù)的可獲得性擬定表1中的評價指標。在考慮人力投入時，與以往的研究不同，我們不僅僅考慮投入的量，還考慮投入人員的素質(zhì)和投入布局，因為這二者都會對效率產(chǎn)生不可忽視的影響。“一般科技人員”是指投入科技人員中非科學家與工程師的那部分；“一般R＆D人員”指R＆D人員中非科學家和工程師的那部分，其他解釋類似。在產(chǎn)出指標中的“科技成果獎勵”我們只統(tǒng)計了國家科技進步獎，省、自治區(qū)、直轄市科技進步獎以及國務(wù)院各部門科技進步獎，對于地方高校而言獲獎機會是不均等的，同時，2007年的數(shù)據(jù)表明，地方高校獲得的國家科技進步獎只有二等獎。因此，我們沒有進行獲獎等級的加權(quán)處理。新疆、西藏、青海由于某些指標數(shù)據(jù)缺失，沒有參與分析。本研究的數(shù)據(jù)來源于《2007年高等學校科技統(tǒng)計資料匯編》和《2007年中國統(tǒng)計年鑒》。

表1 高校創(chuàng)新效率評價指標體系

人力投入指標數(shù)量眾多，而且有些指標之間有重復，去掉任何一個指標會使評價失真，而指標之間的重復也會影響評價結(jié)果，為了解決這一問題，首先對人力投入指標進行因子分析，使用軟件為SPSS13.0，采用“Principle Components”提取3個公因子，并對其進行“Direct Oblimin”旋轉(zhuǎn)，使用回歸法計算因子得分系數(shù)矩陣，有關(guān)因子分析的數(shù)字特征描述及相應檢驗結(jié)果①由于篇幅限制相關(guān)的分析結(jié)果及因子命名沒有在文中給出，對此有興趣的讀者可以向作者索要。見表2。分析結(jié)果說明9個人力投入指標不僅適合作因子分析，而且提取的3個公因子能夠全面地反映人力投入指標的信息。因此，在下面的分析中我們用3個因子得分替代9個人力投入指標，因子得分有負值存在，在進入計算之前3個因子得分需要進行處理，使每個因子的最低得分不小于零。

表2 因子分析特征描述及檢驗結(jié)果

三、結(jié)果與分析

（一）第一階段SDEA結(jié)果分析

如果運用傳統(tǒng)的DEA分析，那些處于效率前沿的地區(qū)高校的創(chuàng)新效率值無法進一步區(qū)分，給第二階段的分析造成較大的誤差，為此，該階段我們采用SDEA模型，分析軟件為EMS1.3，分析條件選擇規(guī)模報酬可變、投入主導。效率值列于表3中，同周靜［4］110－117的研究結(jié)論相似，地方高校科技創(chuàng)新有效區(qū)域并不一定分布在經(jīng)濟相對發(fā)達地區(qū)，在偏遠或欠發(fā)達地區(qū)高校的創(chuàng)新效率也可以達到相對有效。其中，北京、云南、河南、陜西、寧夏五個地區(qū)高校的創(chuàng)新效率值比較高，通過觀察這些地區(qū)高校的經(jīng)費投入方向和產(chǎn)出分布可以發(fā)現(xiàn)：陜西同其他四個地區(qū)不同，它的“研發(fā)經(jīng)費投入”較“R＆D成果應用及科技服務(wù)經(jīng)費”低，或者說將較多的經(jīng)費投入到R＆D成果應用及科技服務(wù)活動中，它的成果中“技術(shù)轉(zhuǎn)讓金額”遠遠高于其他地區(qū)，而另外四個地區(qū)尤其是河南，它的產(chǎn)出高效率主要集中在“學術(shù)論文”和“科技著作”上。

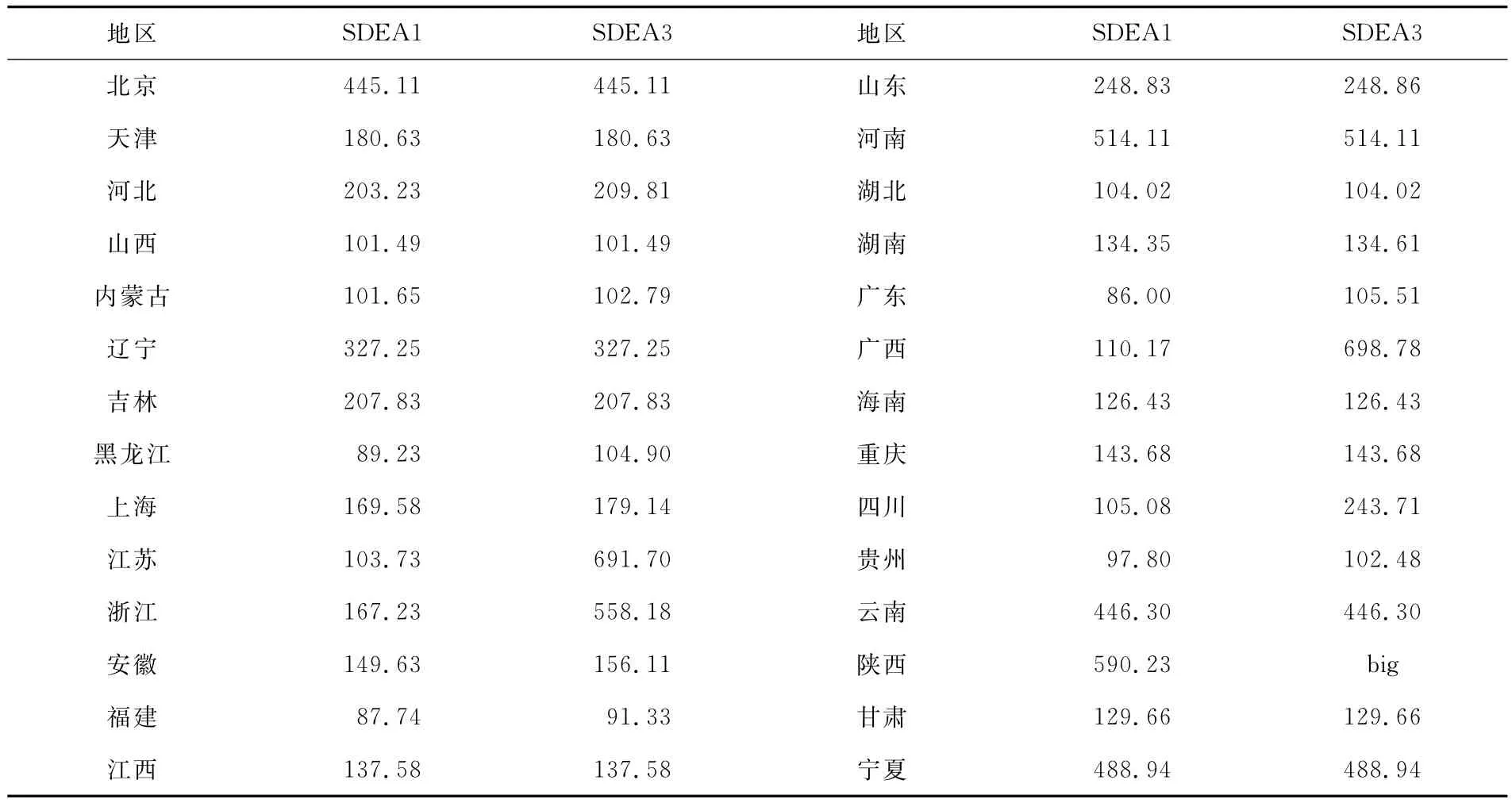
表3 第一階段和第三階段SDEA分析結(jié)果

（二）第二階段的O.L.S.回歸分析結(jié)果

我們以第一步分析得到的效率值為因變量，以環(huán)境指標為自變量用SPSS13.0軟件進行回歸分析，結(jié)果示于表4中，由標準化回歸系數(shù)可以看出：同第一階段的發(fā)現(xiàn)吻合，一個地區(qū)的經(jīng)濟發(fā)展水平（人均GDP）以及科技活動經(jīng)費中政府撥款所占的比例均對地方高校的科技創(chuàng)新效率幾乎沒有影響；而高校中的研發(fā)機構(gòu)數(shù)量對效率有促進作用，相同的人力和經(jīng)費投入，研發(fā)機構(gòu)數(shù)越多創(chuàng)新效率越高；相反，同樣的投入，項目數(shù)越多效率越低。

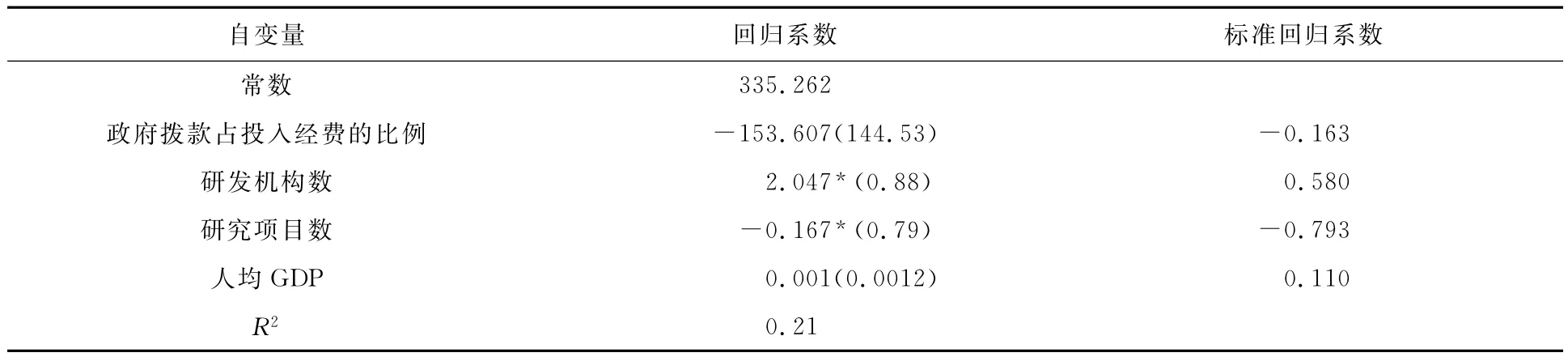
表4 O.L.S.回歸結(jié)果

為了進一步對效率的影響因素進行考查，我們又將“研發(fā)人員中高級職稱所占的比例”、“研發(fā)經(jīng)費占投入經(jīng)費的百分比”、“參加項目的研究生與項目參加人員的比例”以及國際交流的有關(guān)表征指標代入回歸模型，分析結(jié)果顯示：這些因素對本文效率評價體系下進行的效率評價沒有影響。“研發(fā)人員中高級職稱所占的比例”表征的是研發(fā)人員的素質(zhì)，因為在人力投入中我們已經(jīng)考慮了工程師和科學家的人數(shù)；而“研發(fā)經(jīng)費占投入經(jīng)費的百分比”對效率評價沒有影響，這一點在第一階段的結(jié)果分析中我們有同樣的發(fā)現(xiàn)，陜西的研發(fā)經(jīng)費比例相對較低，但效率是最高的，可能是因為“專利出售金額”和“技術(shù)轉(zhuǎn)讓金額”與“R＆D成果應用及科技服務(wù)經(jīng)費”的高低有關(guān)。

（三）第三階段的DEA分析結(jié)果

依據(jù)式（2）和表4的分析結(jié)果計算環(huán)境指數(shù)①因為這里分析的是總體，不涉及由樣本到總體的推斷，不具備統(tǒng)計顯著性的環(huán)境因素仍然參與環(huán)境指數(shù)的計算，因為影響甚微，不會對計算結(jié)果產(chǎn)生影響。，由于本研究中的環(huán)境指數(shù)是負值，也就是說對于所有的地區(qū)環(huán)境綜合影響都是負的，只是影響程度高低而已。因此，環(huán)境指數(shù)在作為“投入”之前需要對該指數(shù)進行轉(zhuǎn)換處理，處理后環(huán)境指數(shù)最低的地區(qū)為零，其他地區(qū)均大于零。第三階段SDEA分析的結(jié)果（表3）表明：四川、浙江、江蘇、廣西這四個地區(qū)的高校的創(chuàng)新效率在剔除了環(huán)境指數(shù)的影響之后大幅度提升，環(huán)境指數(shù)實際上反映的是“研發(fā)機構(gòu)數(shù)”和“研究項目數(shù)”的影響，通過仔細觀察這四個地區(qū)的兩個指標數(shù)據(jù)可以發(fā)現(xiàn)：浙江、廣西這兩個地方的高校研發(fā)機構(gòu)少，同時研究項目太多是制約效率提升的主要因素；江蘇和四川這兩個地方的地方高校創(chuàng)新效率的制約因素則為研究項目太多，因此在不改變投入的情況下，對于浙江和廣西既要考慮增加地方高校的研發(fā)機構(gòu)數(shù)又要減少研究項目的數(shù)量；而對于江蘇和四川則只要考慮在不改變經(jīng)費投入的情況下，減少研究項目便可以使效率大幅度提升。除了上述四個地區(qū)外，其他地區(qū)沒有影響或影響甚微。

本文運用超效率三階段DEA分析對全國28個地區(qū)的地方高校的科技創(chuàng)新效率進行了評價分析，同時對本文擬定的效率評價指標體系下效率的影響因素進行了回歸分析，研究發(fā)現(xiàn)：地方高校的科技創(chuàng)新效率不受地區(qū)經(jīng)濟發(fā)展水平、教育水平的影響；地方高校的科技活動經(jīng)費主要來源于政府撥款和企業(yè)委托，在我們的效率評價體系中，二者的比例對效率評價不產(chǎn)生影響。“研發(fā)經(jīng)費占投入經(jīng)費的百分比”、“參加項目的研究生與項目參加人員的比例”以及國際交流的頻度對效率評價均無影響。在投入不變的情況下，高校內(nèi)的研發(fā)機構(gòu)數(shù)量對效率產(chǎn)生正的影響，而研究項目的數(shù)量對效率產(chǎn)生負的影響，對于某些地區(qū)，機構(gòu)的數(shù)量少和項目的數(shù)量多制約了效率的提升。

［1］梅軼群，張燕.高校科技創(chuàng)新能力的分析和評價［J］.技術(shù)經(jīng)濟，2006，25（6）：74－77.

［2］梁燕.廣東省高校科技創(chuàng)新能力比較研究［J］.高教探索，2009（4）：58－62.

［3］王光平，金浩.基于因子分析的高校科技創(chuàng)新能力的實證研究［J］.河北師范大學學報：哲學社會科學版，2008（4）：48－51.

［4］周靜.我國不同地區(qū)高校科技創(chuàng)新的制度效率與規(guī)模效率研究［J］.研究與發(fā)展管理，2005，17（1）.

［5］張海燕.2002－2005年間我國不同地區(qū)高校科技創(chuàng)新效率比較研究［J］.科技進步與對策，2007，24（11）：109－114.

［6］智曉東.指標相關(guān)性對DEA評價效用的影響［J］.統(tǒng)計研究，2009（6）：40－44.

［7］Fried H O，Lovell C A K，Schmidt S S，Yaisawarng S.Accounting for environmental effects and statistical noise in data envelopment analysis［J］.Journal of Productivity Analysis，2002（17）：157－174.

［8］Michael F.Gormana，John Ruggiero.Evaluating US state police performance using data envelopment analysis［J］.Int.J.Production Economics 2008（113）：1031－1037.

Evaluation of S＆T Innovation Efficiency of Chinese Provincial Colleges：A Three Stage DEA－Based Study

LI Ying1，CUI Yu－wei2
（1.Zhou Enlai School of Government，NanKai University，Tianjin 300071，China；2.Tianjin Meteorological Bureau，Tianjin 300074，China）

The article attempts to make factor analysis of human inputs to take three common factors using science and technology data of Chinese provincial colleges in 2007.Then the three stage DEA is used to evaluate S＆T innovation efficiency of 28higher learning institutions and to analyze the factors relative to efficiency as well.From the study above we come to conclusion that local economy，cultural progress and government funding for research are not relative to efficiency.However，number of colleges and research programs underway in some areas are decisive factors for it.

Provincial Colleges；S＆T Innovation Efficiency；Factor analysis；Three stage DEA；SDEA

G40

A

1001－6201（2011）02－0177－05

［責任編輯：何宏儉］

2010－10－20

南開大學亞洲基金（ASI002）

李瑛（1966－），女，山東煙臺人，南開大學周恩來政府管理學院行政管理系副教授，理學博士；崔宇威（1988－），女，黑龍江伊春人，南開大學周恩來政府管理學院研究生。