Leslie人口年齡結構模型的修正

張 良， 時書麗， 竇春軼

（1.沈陽大學理學院，沈陽 110044； 2.遼寧大學信息科學與技術學院，沈陽 110036）

Leslie人口年齡結構模型的修正

張 良1， 時書麗2， 竇春軼2

（1.沈陽大學理學院，沈陽 110044； 2.遼寧大學信息科學與技術學院，沈陽 110036）

Leslie人口年齡結構數學模型建立在沒有人口流動的基礎上，本文試圖建立含人口遷徙因素在內的修正模型，并研究修正模型年齡結構的穩定性.

年齡結構；Leslie矩陣；特征根；特征向量；冪法

1 Leslie年齡結構模型回顧

二十世紀四十年代末，Leslie建立了在與外界隔絕的封閉系統內，通過初始人口的數量及其年齡分布預測該系統未來某時刻人口的數量及年齡分布的數學模型［1－3］.

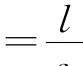
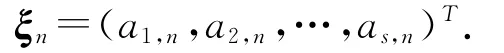
不妨假設下列的數據bk，d k（k＝1，2，…，s）及mk（k＝1，2，…，s－1）可根據統計資料得到：

bk為在單位時間段T內第i個年齡分類平均每個女性所生殖的后代數量；

d k為第k個年齡分類人口中女性所占比例；

mk為第k個年齡分類能活過單位時間段T而變成第k＋1年齡分類的比例.

顯然bk≥0，0≤d k≤1，k＝1，2，…，s；0＜mk≤1，k＝1，2，…，s－1.

于是可以導出下列關系式：

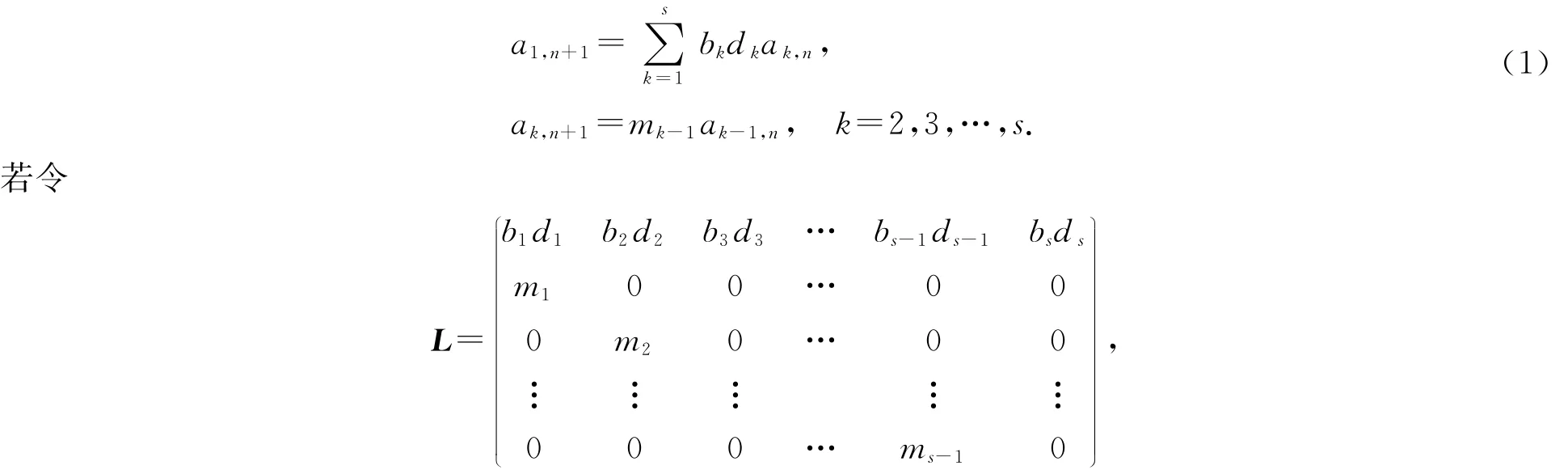
稱其為Leslie矩陣，則（1）式可用矩陣表示為

如果當前的年齡結構向量ξ0為已知，則由（2）式，就得到Leslie年齡結構模型：

2 Leslie年齡結構模型的修正

現今世界人口流動頻繁，幾乎找不到與外界隔絕的封閉地域.所以有必要對Leslie年齡結構模型進行修正.

假設

αk表示由系統外進入該系統第k年齡分類的人數占第k年齡分類的人口總數的比例；

βk表示退出該系統而進入其它系統年齡屬于第k年齡分類的人數占第k年齡分類的人口總數的比例.

不妨設

（i）0≤αk，βk＜1，k＝1，2，…，s；

（ii）在該系統生育的屬于第一年齡分類小孩總是隨其母親進入或退出系統.

于是

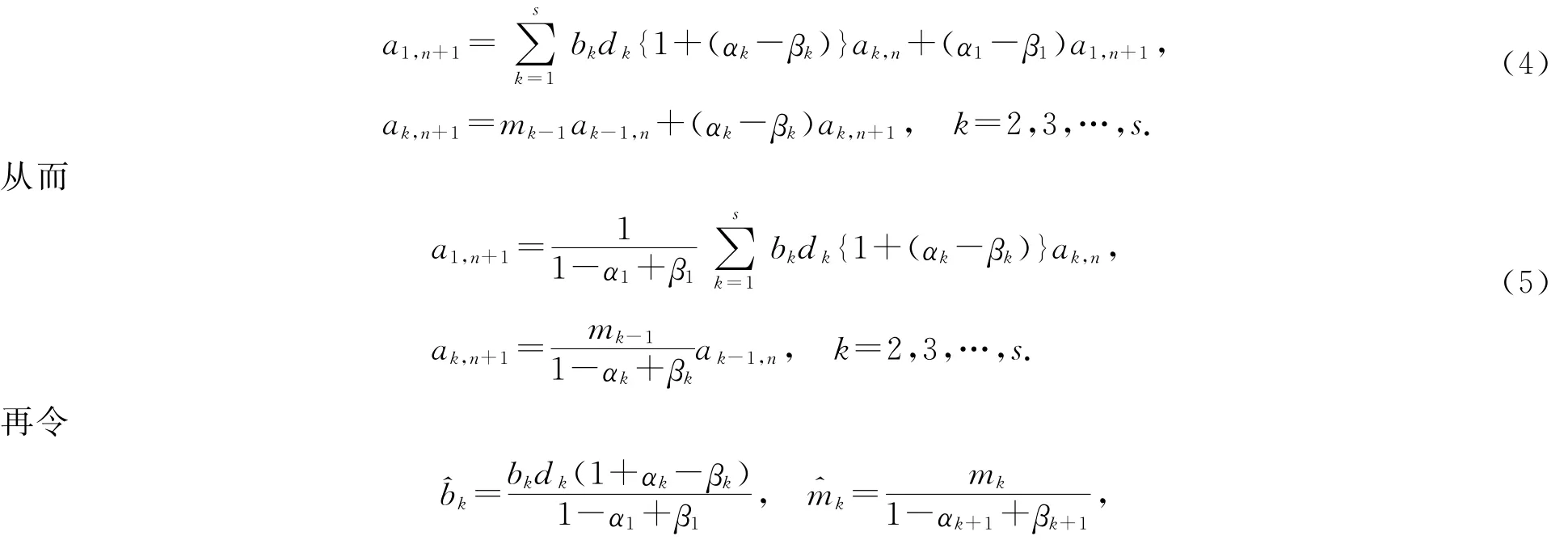
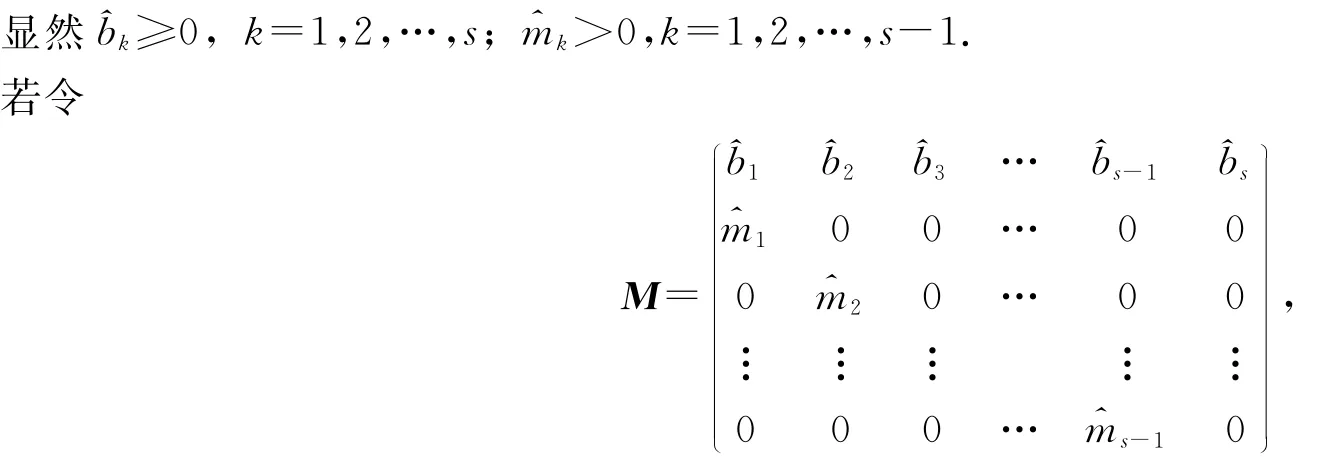
稱M為Leslie的修正矩陣，于是（5）式可用矩陣表示為

從而得到Leslie年齡結構的修正模型：

3 年齡結構的穩定性

當n很大時，向量Mnξ0將如何變化？即修正模型年齡結構的穩定性［4－5］.下面我們借助線性代數與矩陣計算方法來研究它［6－10］.

設矩陣M的特征方程f（λ）＝det（λI－M）＝0，將行列式det（λI－M）按第一行展開后整理得

若λ≠0，則特征方程可變形為

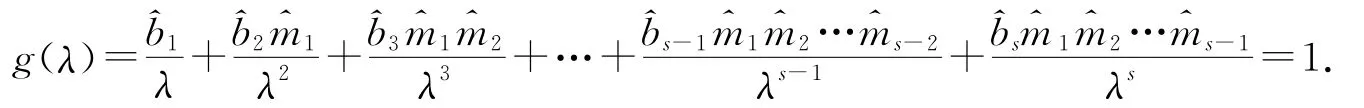
矛盾.所以矩陣M有唯一占優特征根.

定理2修正矩陣M有嚴格占優特征根.

證由定理1知M有唯一占優特征根λ0，對M的任意其它特征根λ，則｜λ｜≤λ0.若｜λ｜＝λ0，由于M的第一行中必有兩個相鄰的元素＾b i與＾b i＋1不為零（只要時間段——期的取法適當，所有相鄰的年齡分類的女性不可能都不生育或者都是男性），因此

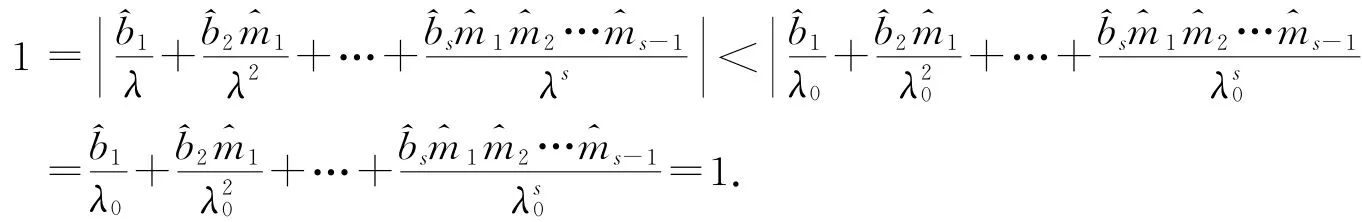
矛盾，因此｜λ｜＜λ0.

對于修正矩陣M的嚴格占優特征根λ0及對應的特征向量x0，可采用矩陣計算之冪法求得：

設M的特征根λi（i＝0，1，2，，…，s－1）滿足條件

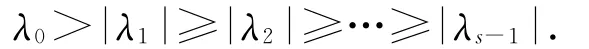
它們對應的特征向量依次是x0，x1，x2，…，x s－1，并且假定它們線性無關.其中λ0是M的嚴格占優特征根.

于是當α0≠0，k充分大時，

注 （i）若α0＝0，可更換初始非零向量v0，再迭代；

（ii）在迭代過程中u k除max（u k）是為了避免計算λk0出現溢出現象.

4 結 論

因此我們得到下面諸結論：

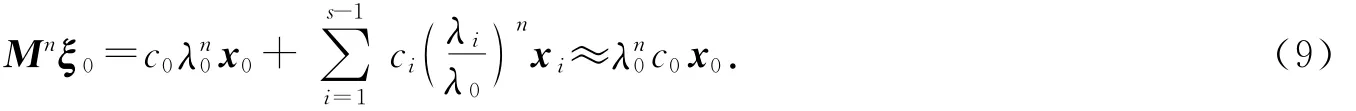
這表明當n充分大時，人口年齡結構按比例穩定在M的唯一的嚴格占優特征根λ0所對應的正的特征向量x0上，而與初始年齡結構ξ0無關.而且通過式（8）可以計算出λ0與x0的近似值.

2.年齡結構是以修正矩陣M的唯一嚴格占優特征根λ0之速率增長.當λ0＜1時，人口數量逐漸減少；λ0＝1，人口數量穩定；λ0＞1，人口數量逐漸增加.

4.上面的結論與方法完全適用于動物、昆蟲等.

［1］Leslie P H.On the use of matrices in certain population mathematics［J］.Biometrika，1945，20（3）：156－168.

［2］姜啟源，謝金星，葉俊.數學模型［M］.北京：高等教育出版社，2004.

［3］Lucas W F.生命科學模型［M］.翟曉燕等，譯.長沙：國防科技大學出版社，1986.

［4］Castro ML，Sliva J A L，Justo D A R.Stability in an age－structured metapopulation model［J］.Journal of Mathematical Biology，2006，52（2）：183－208.

［5］Anatoli V S，Frank C.Models in Population Biology［M］.New York：Springer，2002.

［6］許世壁.談研究年齡結構之數學模型［J］.數學傳播，1983，7（3）：8－10.

［7］蔣爾雄，高坤敏，吳景琨.線性代數［M］.北京：人民教育出版社，1978.

［8］蔣正新，施國梁.矩陣理論及其應用［M］.北京：北京航空學院出版社，1988.

［9］劉玲，葛福生.數值計算方法［M］.北京：科學出版社，2005.

［10］劉文瑜，杜基奎，陳金山.計算方法［M］.北京：科學出版社，2007.

Adjusting Leslie’s Model of Population Age Structure

ZHANGLiang1，SHIShu－li2，DOUChun－yi2
（1.College of Sciences，Shenyang University，Shengyang 110044，China；2.College of the Information Science and Technology，Liaoning University，Shenyang 110036，China）

Leslie established mathematical model of population age structure under the condition of without migration.To correct its defect，an adjusting model with migration is set up and studied its age structure stability.

age structure；Leslie’s matrix；eigenvalue；eigenvector；power method

O29；C92－03

A

1672－1454（2011）04－0099－04

2008－09－28；［修改日期］2008－12－09