與給定多邊形相切的可調廣義Ball閉曲線

高 健， 劉 植

（1.安徽醫科大學衛生管理學院，合肥 230032； 2.合肥工業大學數學學院，合肥 230009）

與給定多邊形相切的可調廣義Ball閉曲線

高 健1， 劉 植2

（1.安徽醫科大學衛生管理學院，合肥 230032； 2.合肥工業大學數學學院，合肥 230009）

討論了與給定控制多邊形相切的分段三次、五次和六次可調廣義Ball曲線的構造方法，所構造的曲線分別是C1，C2和C3連續的，而且對切線多邊形是保形的.曲線上的所有廣義Ball曲線段的控制點由切線多邊形的頂點直接計算產生.給出了在保持公共連接點處相應連續的情況下，內控制點的活動范圍.曲線可以在一定范圍內做局部修改.計算實例表明使用本文的方法靈活、方便、有效.

廣義Ball曲線；切線多邊形；保形曲線

1 引 言

在CAGD及實際應用中人們發現廣義Ball曲線類似于Bézier曲線，有很好的保形性質，且在某些方面，有比Bézier曲線更好的性質［1］.例如：廣義Ball曲線的賦值算法具有穩定的遞歸算法，且2m＋1次廣義Ball曲線的賦值只需2（m＋1）2次乘法和（m＋1）2次加法，而同次數的Bézier曲線需要2（m＋1）（2m＋1）乘法和（m＋1）（2m＋1）次加法（de Casteljau算法）.因此，Bézier曲線繪圖如先轉化為廣義Ball曲線再繪圖，無疑可以大大減少計算量；又如，廣義Ball曲線退化為低一階曲線的充要條件是中間兩個控制點重合，因此很容易判斷，而Bézier曲線的退化條件就要復雜得多；此外，廣義Ball曲線升階可以兩次兩次進行，其計算量只是同次數Bézier曲線升階的一半.因此，在外形設計中，廣義Ball曲線越來越受到重視，有著廣泛的應用價值 .

在CAD，CAGD及逼近的設計過程中，通常會先根據尺寸要求確定控制點，再根據控制點用直線段繪制樣片的大體輪廓，即控制多邊形，在多邊形內用直線和曲線繪制封閉的圖形.由于樣片的形狀不規則，即構成樣片的曲線比較復雜，為了使曲線光順、有彈性，且易于修改，經常會遇到曲線與控制多邊形相切的問題.構造與給定控制多邊形相切的曲線問題，已經有不少文章對之進行了詳述的討論，且在實踐中得到了應用［2－8］.文［7，8］構造了C1，C2和C3連續的廣義Ball曲線，但其中C1和C2連續的曲線只能通過調節切點的位置進行局部修改，從而降低了局部修改的靈活性，且C3連續的廣義Ball曲線是唯一確定的，不可能做局部修改.本文主要研究了與給定多邊形相切的廣義Ball曲線，基于構造組合曲線的可控性，給出更加靈活的構造方法.所構造的C1，C2連續的廣義Ball曲線除了可以調節切點位置外還可以通過調節其內控制點參數對曲線做局部修改，使得曲線的局部修改更加靈活、方便、有效.且本文構造的C3連續的廣義Ball曲線的局部修改也是簡單方便的.計算實例表明本文的方法是可行的.

2 與給定多邊形相切的C1可調廣義Ball閉曲線

對于給定的閉的多邊形〈V0，V1，…，V n〉，其中V n＝V0.假設待構造的分段三次廣義Ball曲線在切線多邊形的第i條邊V i V i＋1上的切點為

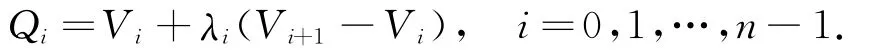
本節目的是希望在每相鄰兩切點Qi，Qi＋1之間構造一段三次廣義Ball曲線ri（t）（i＝0，1，…，n－1），其相應的控制點選取為

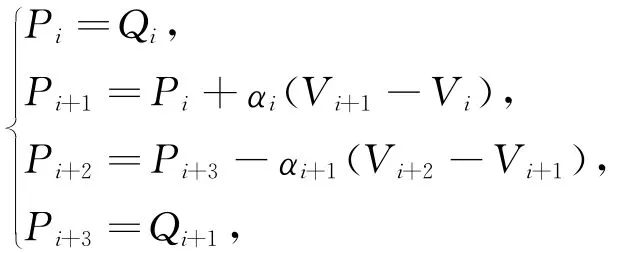
其中切點調節參數αi＜λi＜1－αi.αi為內控制點的調節參數，它滿足

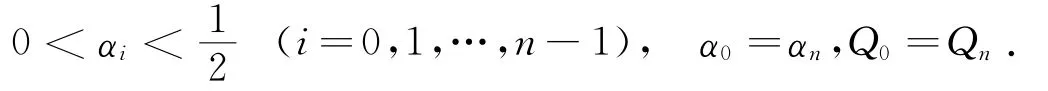
相應的三次廣義Ball曲線段為

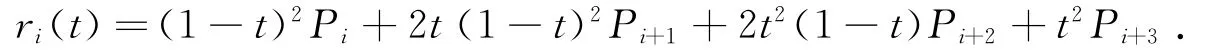
由三次廣義Ball曲線的端點性質［9］，則有

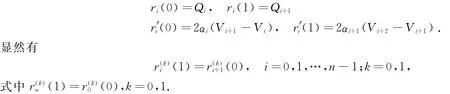
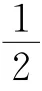
設V i＋1是切線多邊形的轉折點，即矢量V i－1V i×V i V i＋1與矢量V i V i＋1×V i＋1V i＋2方向相反，這時第i－1段與第i段曲線凸性相反，且在切點Qi處形成一個拐點，因此上面構造的分段三次廣義Ball曲線拐點個數與切線多邊形的轉折點個數相等.即該曲線對其給定切線多邊形是保形的.

由此可知，上面構造的分段三次可調廣義Ball閉曲線是C1連續的，保形的且與每條邊V i V i＋1相切.

例1給定平面上一非凸的切線六邊形，用上述算法繪制與給定六邊形每邊相切三次廣義Ball曲線的三個圖形.圖1中的圖形分別是λi＝0.45，αi＝0.4；λi＝0.55，αi＝0.4；λi＝0.55，αi＝0.3.

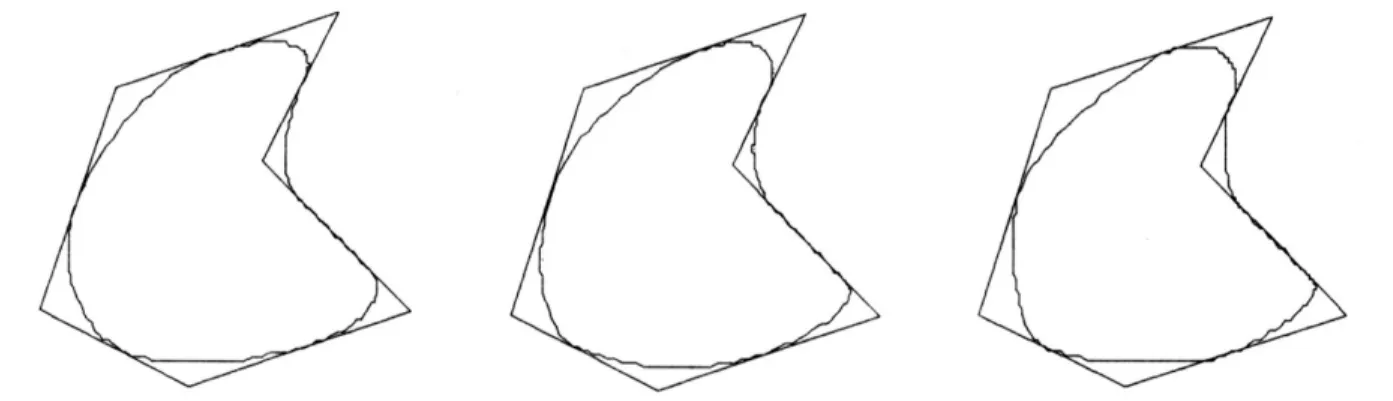
圖1 λi，αi取不同值時的三次廣義Ball曲線

綜上可知，分段三次廣義Ball曲線的形狀由參數λi，αi的選取確定，曲線的切點在一定范圍內可以任意選取.λi增大，切點Qi向V i＋1靠近；λi減小，切點Qi向V i靠近.αi在一定范圍內增大時，內控制點向切線多邊形的頂點靠近，生成的組合曲線相應的向切線多邊形的頂點靠近，否則將遠離頂點.

3 與給定切線多邊形相切的C2可調廣義Ball閉曲線

假設給定的閉的多邊形〈V0，V1，…，V n〉，其中V n＝V0.待構造的分段五次廣義Ball曲線在切線多邊形的第i條邊V i V i＋1上的切點為

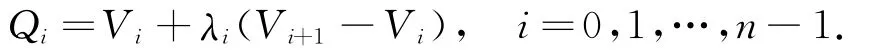
本節目的是希望在每相鄰兩切點Qi，Qi＋1之間構造一段五次廣義Ball曲線ri（t）（i＝0，1，…，n－1），其相應的控制點選取為

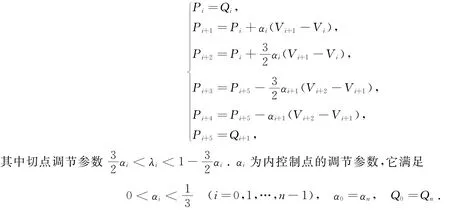
相應的五次廣義Ball曲線段為

由此可知，上面構造的分段五次可調廣義Ball閉曲線是C2連續的，類似第一節的證明，可知構造的分段五次可調廣義Ball閉曲線是保形的，且與每條邊V i V i＋1相切.

例2給定平面上一非凸的切線七邊形，用上述算法繪制與給定七邊形每邊相切五次廣義Ball曲線的三個圖形.圖2中的圖形分別是λi＝0.52，αi＝0.32；λi＝0.52，αi＝0.22；λi＝0.65，αi＝0.22

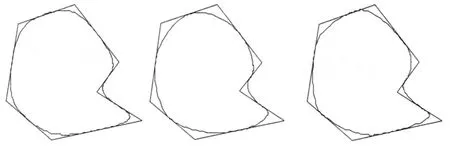
圖2 λi，αi取不同值時的五次廣義Ball曲線

綜上可知，分段五次廣義Ball曲線的形狀由參數λi，αi的選取確定，曲線的切點在一定范圍內可以任意選取.λi增大，切點Qi向V i＋1靠近；λi減小，切點Qi向V i靠近.αi在一定范圍內增大時，內控制點向切線多邊形的頂點靠近，生成的組合曲線相應的向切線多邊形的頂點靠近，否則將遠離頂點.

4 與給定切線多邊形相切的C3可調廣義Ball閉曲線

我們仍假設對于給定的閉的多邊形〈V0，V1，…，V n〉，其中V n＝V0.待構造的分段六次廣義Ball曲線在切線多邊形的第i條邊V i V i＋1上的切點為

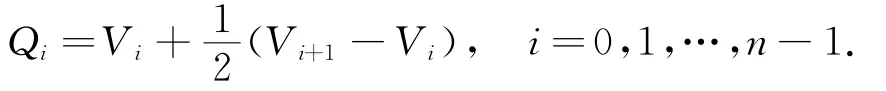
本節目的是希望在每相鄰兩切點Qi，Qi＋1之間構造一段六次廣義Ball曲線ri（t）（i＝0，1，…，n－1），其相應的控制點選取為

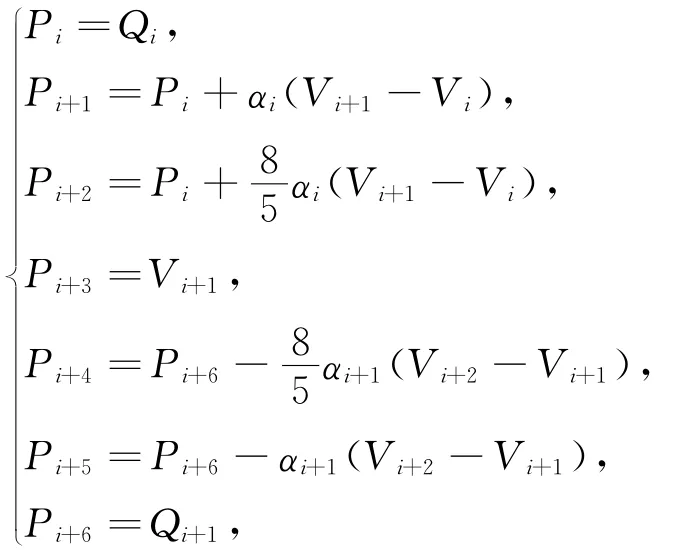
其中αi為內控制點的調節參數，它滿足

相應的六次廣義Ball曲線段為

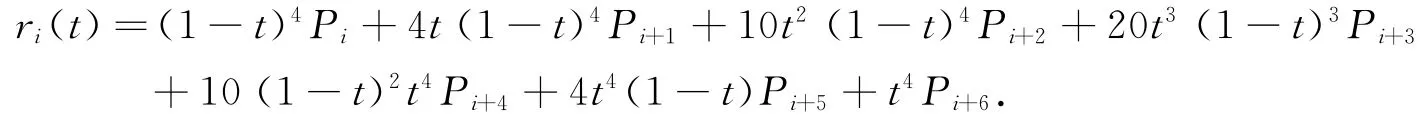
由六次廣義Ball曲線的端點性質［9］，則有

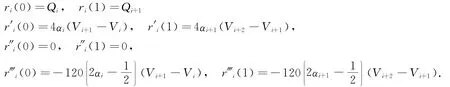
顯然有

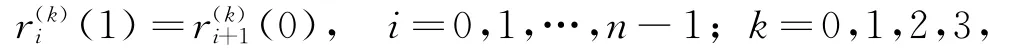
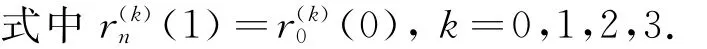
由此可知，上面構造的分段六次可調廣義Ball閉曲線是C3連續的，類似前面證明，可知構造的分段六次可調廣義Ball閉曲線是保形的，且與每條邊V i V i＋1相切.

例3給定平面上一非凸的切線七邊形，用上述算法繪制與給定七邊形每邊相切六次廣義Ball曲線的三個圖形.圖3中的圖形分別是αi＝0.1；αi＝0.2；αi＝0.3

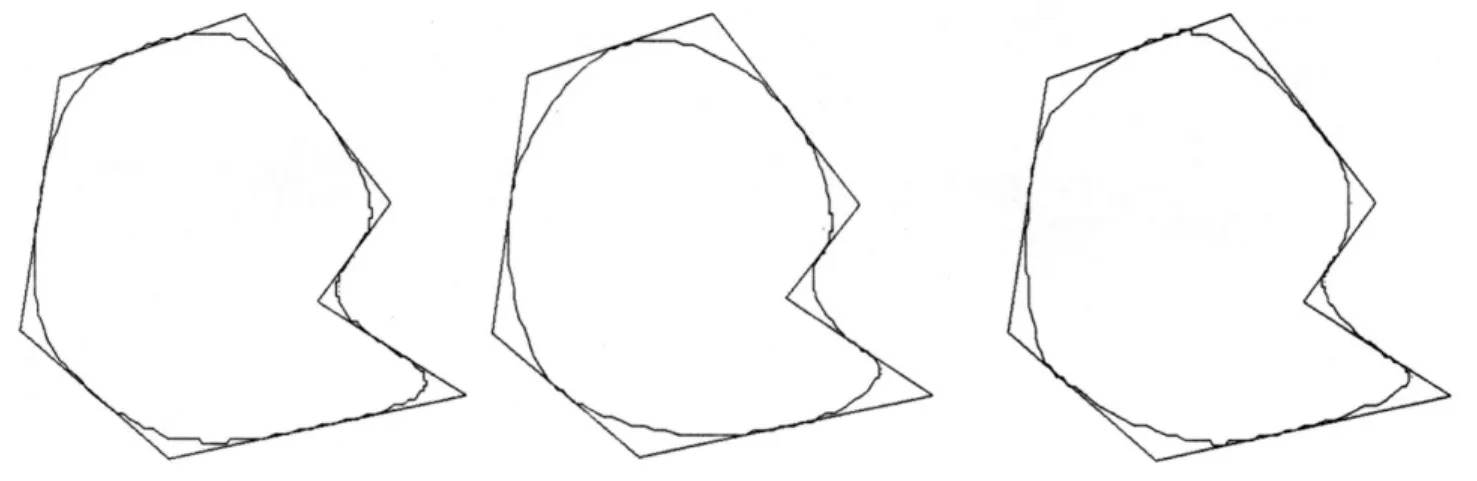
圖3 αi取不同值時的六次廣義Ball曲線

綜上可知，分段六次廣義Ball曲線的切點位置是確定的.曲線的形狀由參數αi的選取確定.αi在一定范圍內增大時，內控制點向切線多邊形的頂點靠近，生成的組合曲線相應的向切線多邊形的頂點靠近，否則將遠離頂點.

5 結 論

用本文構造的與給定多邊形每邊相切的廣義Ball曲線，與傳統的方法相比，它具有以下優點：

（i）本文構造的曲線只要給定多邊形以及各調節參數的值，即可構造曲線，無需額外信息，從而大大減少了計算量.

（ii）所構造的三次、五次和六次廣義Ball曲線分別是C1，C2和C3連續的，光滑性好.

（iii）所構造的曲線不僅與給定多邊形的每條邊相切，而且對多邊形具有保形性，避免了曲線產生多余的拐點.

（iv）可以在形狀參數的取值范圍內選擇不同的參數值，進行曲線設計.無論是曲線內控制點的調整，還是切點控制參數的改變，都是對曲線具有局部性的，曲線修改十分方便.

［1］丁友東，李敏.廣義Ball曲線的性質及應用［J］.應用數學學報，2000，23（4）：580－595.

［2］Hering L.Closed（C2＿andC3＿Continuous）Bézier and B－spline curve with given tangent polygons［J］.CAD，1983（1）：3－6.

［3］Fang K.Closed（G2＿Continuous）Bézier curve with given tangent polygon［J］.Chinese Journal of Numerical Mathematics，1991，3（2）：34－38.

［4］方逵，蔡放，譚建容.帶有給定切線多邊形的C2和C3Bézier閉樣條曲線［J］.計算機輔助設計與圖形學報，2000，12（5）：330－332.

［5］劉植.與給定切線多邊形相切的C3Bézier可調閉樣條曲線［J］.合肥工業大學學報，2005，28（5）：223－224.

［6］閆德勤.與給定多邊形相切的四次可控C2Bézier曲線［J］.計算機應用與軟件，2003，3（5）：52－64.

［7］王成偉姚云.與給定多邊形相切的C1廣義Ball閉曲線［J］.北京服裝學院學報，2002，22（1）：71－74.

［8］王成偉.與給定多邊形相切的C2和C3廣義Ball閉曲線［J］.高等學校計算數學學報，2002，24（4）：349－354.

［9］王國瑾，汪國昭，鄭建民.計算機輔助幾何設計［M］.北京：高等教育出版社，2001：100－112.

Closed Adjustable Generalized Ball Curves with Given Tangent Polygon

GAOJian1，LIUZhi2
（1.Health Management College，Anhui Medical University，Hefei 230032，China；2.School of Mathematics，Hefei University of Technology，Hefei 230009，China）

This paper proposes an approach of constructing planar piecewise closed generalized Ball curve of 3th、5th and 6th degree with all edges tangent to a given control polygon and the curve segments can be joined together withC1，C2andC3continuity respectively.The control points of the generalized Ball curve segments are computed simply by the vertices of the given tangent polygon.The admissible scope of the inner control points is given in order to guarantee corresponding continuity.Local modifications for these curves are possible.The effectiveness as well as adaptability of the method is manifested by experimental results.

generalized Ball curve；tangent polygon；shape－preserving curve

TP241.3

A

1672－1454（2011）04－0042－05

?

2008－03－31