切變基本緯向流中β效應的赤道Rossby孤立波包*

宋 健 姜 楠 楊聯貴

1)(內蒙古工業大學理學院，呼和浩特 010051)

2)(天津大學機械學院，天津 300072)

3)(內蒙古大學數學科學學院，呼和浩特 010021)

(2010年1月18日收到;2010年4月15日收到修改稿)

切變基本緯向流中β效應的赤道Rossby孤立波包*

宋 健1)姜 楠2)楊聯貴3)?

1)(內蒙古工業大學理學院，呼和浩特 010051)

2)(天津大學機械學院，天津 300072)

3)(內蒙古大學數學科學學院，呼和浩特 010021)

(2010年1月18日收到;2010年4月15日收到修改稿)

從描寫赤道Rossby波的正壓大氣位渦方程出發，采用多重尺度攝動方法推導出在切變基本緯向流中具有β效應的非線性赤道Rossby波包演變滿足非線性Schr?dinger方程，并得到單個包絡孤立子波解，分析了基本切變流，β效應對非線性赤道Rossby波的影響.

赤道Rossby波，β效應，非線性Schr?dinger方程，包絡孤立子

PACS:47.35.Fg，92.10.Ei，92.70.Cp

1.引 言

大氣動力學中，Rossby波是指生命史很長結構上有組織的前后一致的大尺度永久性波動，并且這些波動具有穩定的、大振幅的孤立波特征.特別是熱帶大氣運動與全球氣候變化有密切聯系，人們對熱帶大氣運動規律有許多新的認識，其中熱帶大氣波動理論是低緯度大氣動力學研究的重要內容.Matsuno［1］在1966年做了開創性的研究，得到在赤道β平面大氣運動的線性波動，并分析研究了它們的特性.Domaracki和 Loesch［2］，Ripa［3］研究了赤道波與波之間的相互作用.Body［4—6］給出了非線性Kelvin波，并利用攝動方法從赤道β平面淺水模式原始方程導出小振幅赤道Rossby波隨時間的演變滿足 Korteweg-de Vries(KdV)方程或者 modify Korteweg-de Vries(mKdV)方程，這些研究表明存在赤道Rossby孤立波.然而對于KdV(mKdV)型孤立波是考慮了長波近似(緯向波數k→0)的情況，在實際大氣中，特別是大氣中存在大振幅的Rossby波，長波近似并不成立.Domaracki和 Loesch［2］，Ripa［3］和 Body［7，8］的研究都未涉及基本氣流對赤道波動的影響，這與實際不相符合;趙強和劉式適［9］在考慮基本流切變對赤道波動的影響下，推導出非線性赤道Rossby波包演變滿足非線性 Schr?dinger方程.趙強等［10］還用多重尺度攝動法從赤道 β平面淺水模式出發，描述了赤道Rossby孤立波振幅滿足非線性Schr?dinger方程，并分析了切變緯向流對非線性赤道Rossby孤立波波動的影響，但是他們都沒有考慮β效應(參數 β是緯度變量 y的函數)對赤道Rossby波的影響.Charney和 Straus［11］基于準地轉位渦度方程構造了一個β平面通道中考慮地形、非絕熱加熱和摩擦的正壓大氣模式，這項工作開創了大氣多平衡態非線性動力學的研究.封國林等［12—16］建立了南方濤動與厄爾尼諾循環統一的海-氣振蕩子的隨機動力學模型.達朝究和丑紀范［17］研究了地形隨時間緩變時Rossby波振幅的演變問題.宋健等［18—23］在正壓流體與層結流體中分別給出β效應與地形效應對Rossby孤立波振幅的影響.孤立波解在非線性問題中占有重要地位，給出了許多求孤立波解的方法［24—28］，如 Hirota，s 雙線性方法［29］、橢圓 函 數 展 開 法［30，31］以 及 數 值 方 法［32，33，34］等被廣泛應用.本文中，我們研究了在切變基本緯向流下，參數β隨緯度變化時赤道Rossby孤立波振幅的演變，說明了即使沒有基本氣流切變仍可以由β效應誘導非線性Rossby孤立波.

2.方程的推導

2.1.控制方程與邊界條件

Charney［35］指出，在無凝結潛熱釋放大氣中，熱帶大氣運動是水平和準無輻散的，該模型中只存在Rossby波而濾去了重力波.采用一個簡單的模式方程，其中考慮β隨緯度變量y變化，這樣赤道Rossby的正壓位渦方程［36］為

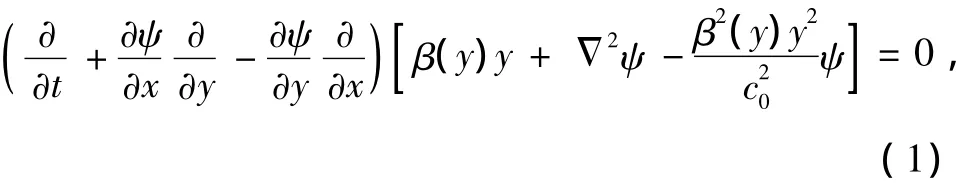
式中，ψ是流函數，Δ2為二維Laplace算子

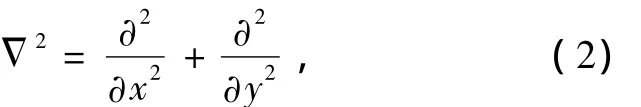
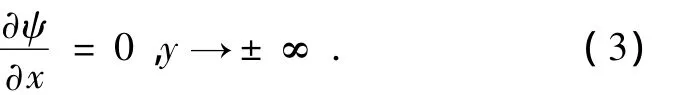
若令

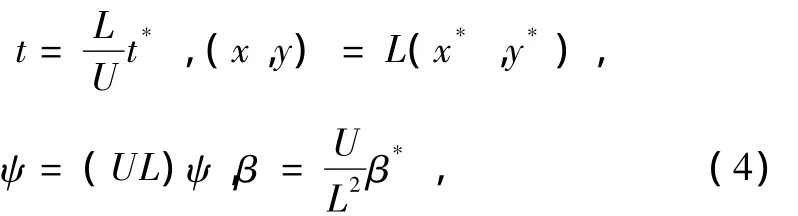
(1)，得到無量綱形式為

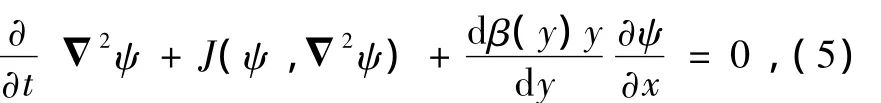
無量綱下的邊界條件為

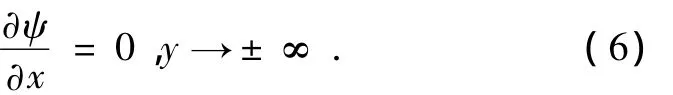
2.2.非線性 Schr?dinger方程

取總流函數為緯向流與擾動流函數的和為

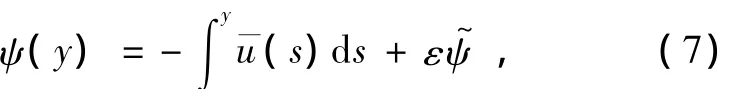
式中，前一項假定基本緯向流僅為y的函數，ε是無量綱赤道 Rossby數，表征非線性的強弱是擾動流函數.將(7)式代入方程(5)和(6)，得到擾動流函數的方程與邊界條件

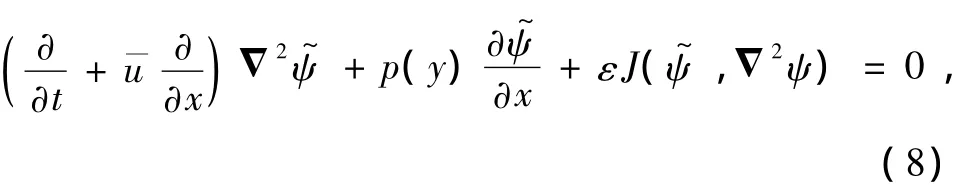
由于地球大氣運動具有多時空尺度的特征，除了快變量x和t外，可以引入如下慢時空變量［2］:

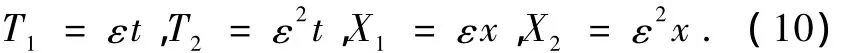
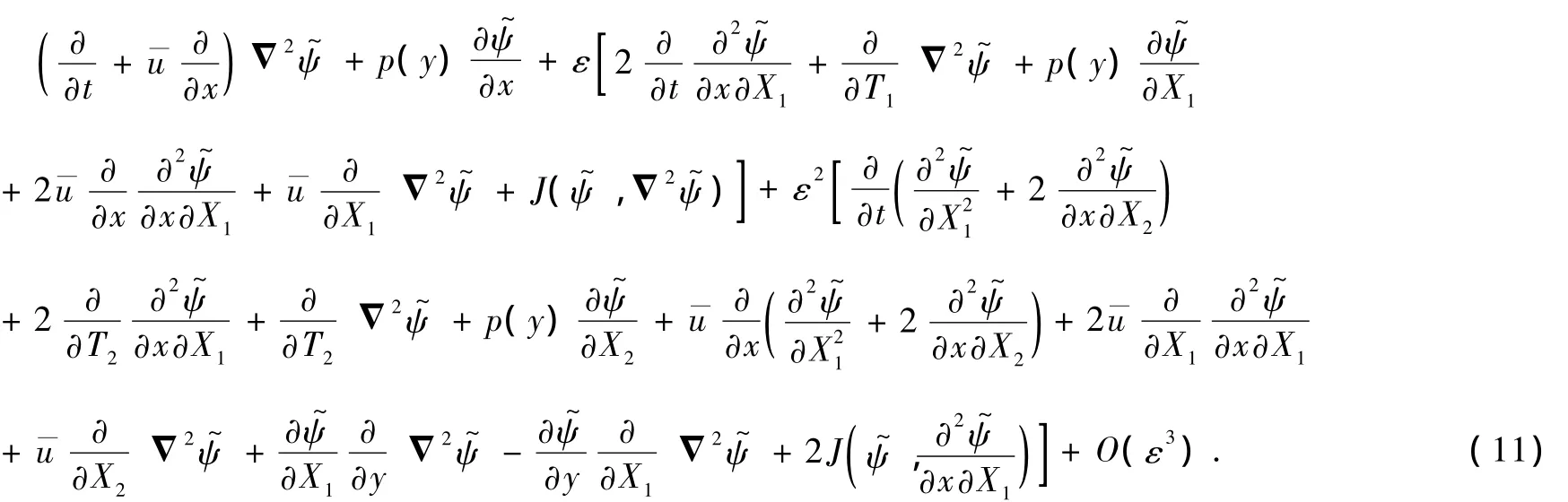
將(10)式代入方程(8)得假設擾動流函數有如下的小參數展開形式［37］:

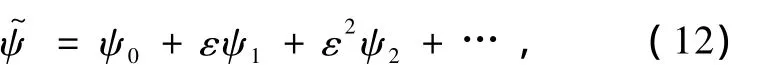
將(12)式代入方程(11)得到各階攝動問題的方程與邊界條件.

對于 O(ε0)階，有

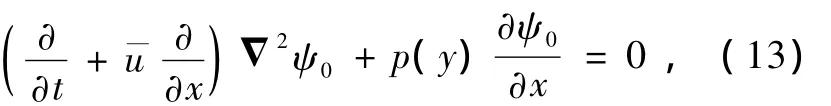
假設ψ0有如下形式的分離變量解

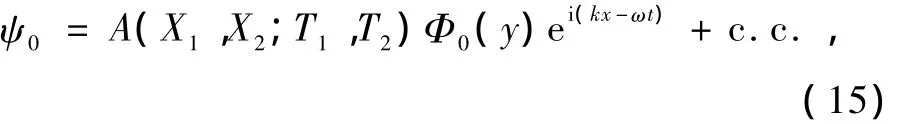
其中 c.c.表示它前項的共軛，A(X1，X2;T1，T2)為復振幅，k為緯向波數.將(15)式代入方程(13)和(14)得

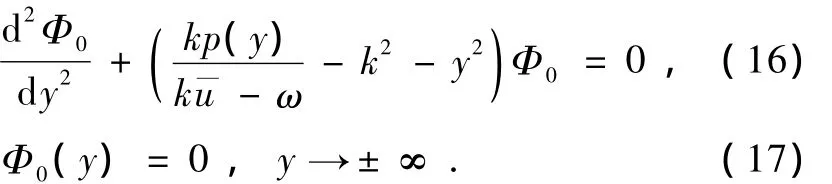
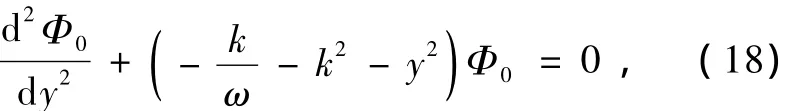
Weber方程的本征值為

其中n為經向模態數.相應的本征函數為

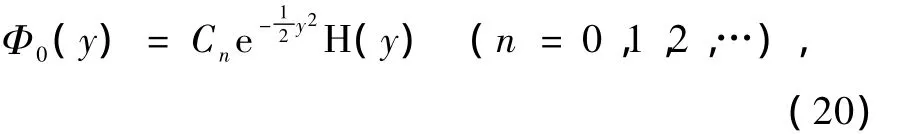
這里Cn為任意常數，Hn(y)是n階Hermite多項式.另外，在本階問題中，只能確定波的空間結構，而不能確定波振幅隨時間的演變.為了確定波振幅 A(X1，X2;T1，T2)的演變，繼續求解高階問題.

對于 O(ε1)階，有

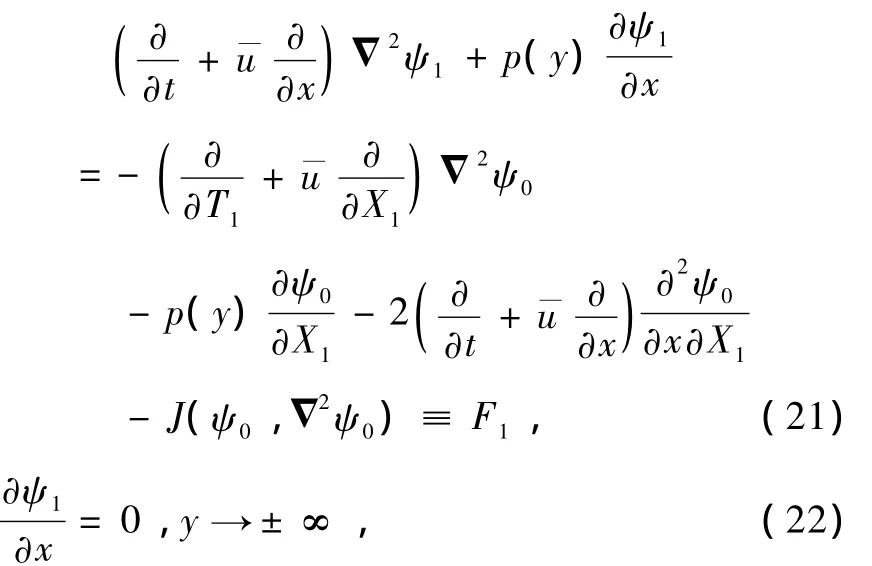
由 ψ0=A(X1，X2;T1，T2)Φ0(y)ei(kx－ωt)+c.c.與方程(16)得

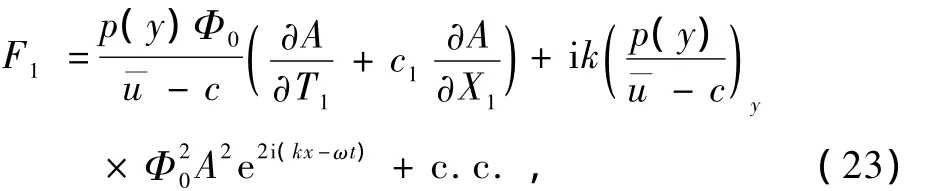
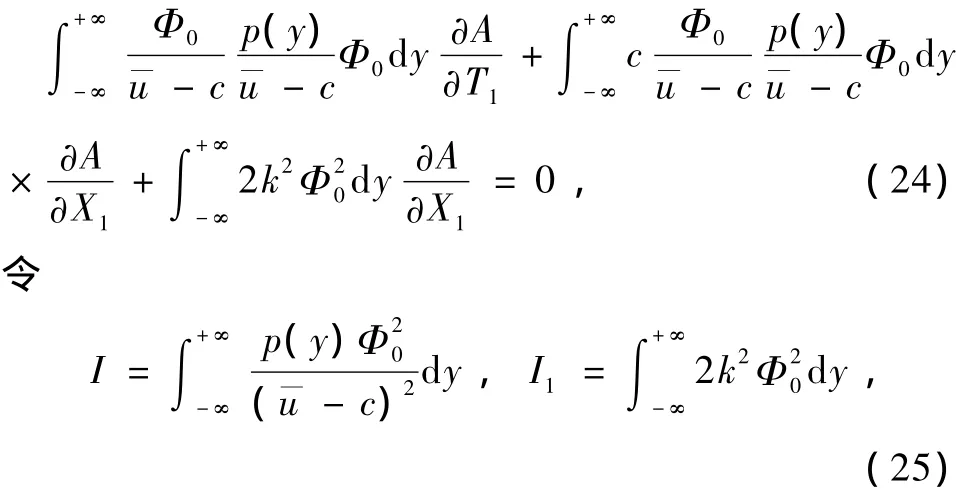
方程(24)簡化為

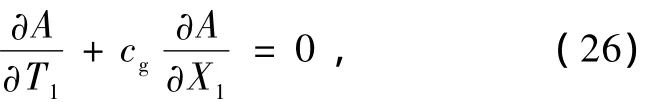
這里

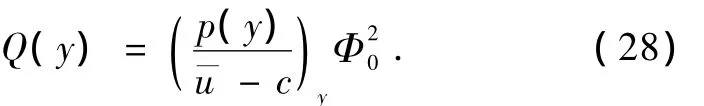
假設方程(27)有如下諧波解

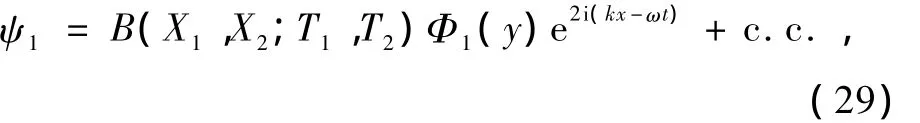
將(29)式代入方程(27)與(22)得

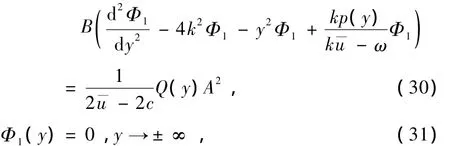
在方程(30)中，A和 B是兩個相互聯系的變量，由于 A和 B都是慢變量 X1，X2，T1，T2的函數，并且 B與A2成比例.不妨設B=A2，則

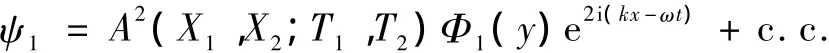
對于 O(ε2)階，有

α和δ分別是頻散系數和非線性系數(即Landau系數)，它們與 β(y)和 u—(y)有關.

方程(38)就是描述切變基本流中β效應下赤道Rossby波包振幅演變的非線性Schr?dinger方程，它反映了赤道Rossby波的特性.做坐標變換［37］

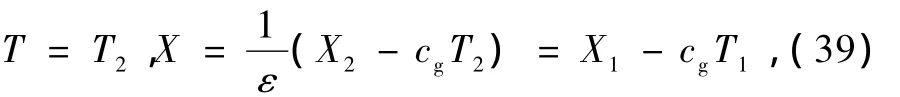
則(37)式化為標準的非線性Schr?dinger方程

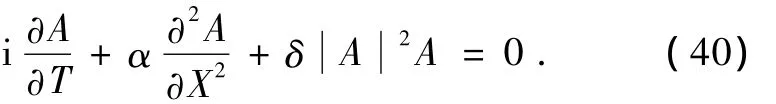
若基本氣流不存在切變(u—=常數)時，當 β是緯度變量 y的函數，由(28)式知 Q(y)≠0，這時 δ≠0，方程(40)仍是非線性 Schr?dinger方程.這說明即使沒有基本氣流水平切變，只要 β效應存在，赤道Rossby波振幅演變也滿足非線性 Schr?dinger方程.只有當基本流無切變，β是常數時，方程(40)中的非線性項消失.

方程(40)有如下單個包絡孤立波解

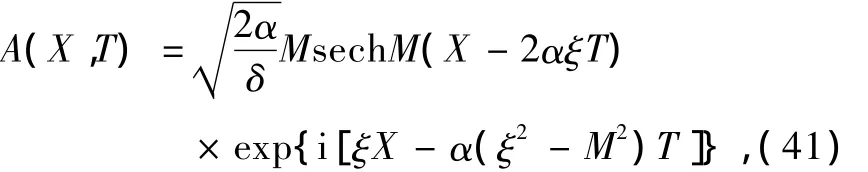
式中M和ξ分別是Rossby包絡孤立波的振幅和移速，它們的值由A(X，T)的初始狀態決定.將(15)和(41)式代入(7)式得

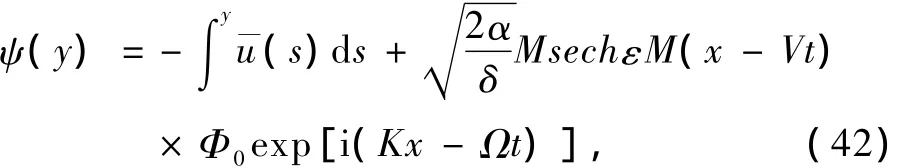
其中

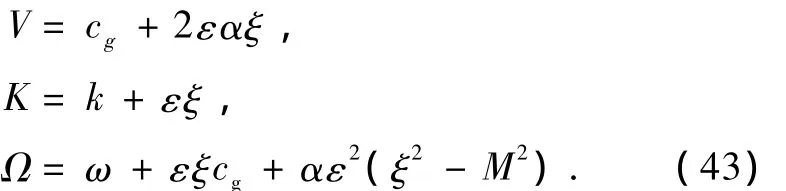
(42)和(43)式說明赤道Rossby包絡孤立波傳播速度V等于線性Rossby波的群速度加上一個小修正量，載波波數K等于線性Rossby波波數k加上一個小修正量，載波頻率Ω等于線性Rossby波的頻率ω加上兩項小修正量且與它的波振幅有關，顯示非線性的特征.這說明赤道大氣中Rossby波與切變基本氣流、β效應的的非線性相互作用，可以使大氣中形成具有sech形狀的孤立子.此外，孤立波的存在還必須有這表示不能產生正壓不穩定［38］.事實上，一旦產生正壓不穩定，就不可能保持恒定波型了.

3.結 論

在正壓流體中，應用多重尺度攝動法，從描寫赤道Rossby波位渦度方程推導出在切變基本緯向流中 β是緯度變量y的函數下，非線性赤道Rossby波包演變滿足非線性 Schr?dinger方程，并得到其包絡孤立波解.這說明赤道大氣中Rossby波與切變的基本氣流，β效應的非線性相互作用，可以使大氣中形成Rossby包絡孤立子，而且這種孤立波是不需要長波近似條件的頻散波.它可以解釋赤道大氣中西移Modons最后通過能量頻散而崩潰消失，并進一步說明即使沒有基本氣流切變，仍由β效應誘導非線性出 Rossby孤立波.基本氣流切變、非線性β效應顯然都是 Rossby孤立波產生的重要因子.

［1］Matsuno T 1966J.Meteor.Soc.Japan44 25

［2］Domaracki A，Loesch A Z 1977J.Atmos.Sci.34 486

［3］Ripa P 1982J.Phys.Oceanogr.12 97

［4］Body J P 1980aJ.Phys.Oceanogr.10 1

［5］Body J P 1980bJ.Phys.Oceanogr.10 1699

［6］Body J P 1984Dyn.Atmos.Oceans8 173

［7］Body J P 1985J.Phys.Oceanogr.15 46

［8］Body J P 1983J.Phys.Oceanogr.13 428

［9］Zhao Q，Liu S K 2001Chin.J.Atmos.Sci.25 133(in Chinese)［趙 強、劉式適2001大氣科學 25 133］

［10］Zhao Q，Fu Z T，Liu S K 2001Adv.Sci.18 418

［11］Chraney J G，Straus D M 1980J.Atmos.Sci.37 1157

［12］Feng G L，Dai X G，Wang A H，Chou J F 2001Acta Phys.Sin.50 606(in Chinese)［封國林、戴新剛、王愛慧、丑紀范2001物理學報 50 606］

［13］Feng G L，Dong W J，Jia X J，Cao H X 2002Acta Phys.Sin.51 1181(in Chinese)［封國林、董文杰、賈曉靜、曹鴻興2002物理學報 51 1181］

［14］Feng G L，Gao X Q，Dong W J，Li J P 2008Chaos Solitons and Fractals37 487

［15］Feng G L，Gong Z Q，Zhi R，Zhang D Q 2008Chin.Phys.B 17 2745

［16］Feng G L，Wang Q G，Hou W，Gong Z Q，Zhi R 2009Acta Phys.Sin.58 2853(in Chinese)［封國林、王啟光、侯 威、龔志強、支 蓉2009物理學報58 2853］

［17］Da C J，Chou J F 2008Acta Phys.Sin.57 2595(in Chinese)［達朝究、丑紀范2008物理學報57 2595］

［18］Song J，Yang L G，Da C J，Zhang H Q 2009Atmos.Ocea.Sci.Lett.2 18

［19］Song J，Yang L G 2009Chin.Phys.B 18 2873

［20］Song J，Yang L G 2009Proc.Geophys.25 543(in Chinese)［宋 健、楊聯貴2010地球物理學進展25 543］

［21］Song J，Yang L G 2010Acta Phys.Sin.59 383(in Chinese)［宋 健、楊聯貴2010物理學報59 383］

［22］Song J，Lai J F 2010Acta Phys.Sin59 4756(in Chinese)［宋健、賴俊峰2010物理學報59 4756］

［23］Song J，Yang L G 2010Plateau Meteor.29 1137

［24］Fan E G，Zhang H Q 1998Acta Phys.Sin.47 353(in Chinese)［范恩貴、張鴻慶 1998物理學報 47 353］

［25］Fan E G，Zhang H Q 2000Acta Phys.Sin.49 1409(in Chinese)［范恩貴、張鴻慶2000物理學報49 1409］

［26］Mao J J，Yang J R 2005Acta Phys.Sin.54 4999(in Chinese)［毛杰健、楊建榮2005物理學報54 4999］

［27］Zhu H P，Zheng C L 2006Acta Phys.Sin.55 4999(in Chinese)［朱海平、鄭春龍 2006物理學報 55 4999］

［28］Chen X F，Mo J Q，Zhang W J 2009Acta Phys.Sin.58 7397(in Chinese)［陳賢峰、莫嘉琪、張偉江 2009物理學報 58 7397］

［29］Mao J J，Yang J R 2007Acta Phys.Sin.56 5049(in Chinese)［毛杰健、楊建榮2007物理學報56 5049］

［30］Liu S D，Fu Z T，Liu S K，Zhao Q 2002Acta Phys.Sin.51 718(in Chinese)［劉式達、付遵濤、劉式適、趙 強2002物理學報 51 718］

［31］Liu S K，Fu Z T，Liu S D，Zhao Q 2002Acta Phys.Sin.51 1923(in Chinese)［劉式適、付遵濤、劉式達、趙 強 2002物理學報51 1923

［32］He W P，Feng G L，Dong W J，Li J P 2004Acta Phys.Sin.53 3258(in Chinese)［何文平、封國林、董文杰、李建平 2004物理學報53 3258］

［33］He W P，Feng G L，Wu Q，Wan S Q，Chou J F 2008Non.Pro.Geophys.15 601

［34］Zhou L，Gong Z Q，Zhi R，Feng G L 2008Acta Phys.Sin.57 7380(in Chinese)［周 磊、龔志強、支 蓉、封國林 2008物理學報57 7380］

［35］Charney J G 1963J.Atmos.Sci.20 607

［36］GillA E 1982Atmosphere-OeanDynamics(San Diego:Academic Press)pp444—447

［37］Jeffrey A，Kawahara T 1982Asymptotic Methods in Nonlinear Waves Theory(Melbourne:Pitman Publishing Inc.)pp256—266

［38］Kuo H L 1949J.Meteor.6 105

PACS:47.35.Fg，92.10.Ei，92.70.Cp

Equatorial Rossby envelope solitary waves withβeffect in a shear flow*

Song Jian1)Jiang Nan2)Yang Lian-Gui3)?
1)(College of Sciences，Inner Mongolia University of Technology，Hohhot 010051，China)
2)(School of Mechanical Engineering，Tianjin University，Tianjin 300072，China)
3)(School of Mathematical Science，Inner Mongolia University，Hohhot 010021，China)
(Received 18 January 2010;revised manuscript received 15 April 2010)

With a simple model of shallow-water on an equatorial beta plane，the nonlinear equatorial Rossby waves in a shear flow with beta effect are investigated by the asymptotic method of multiple scales.The nonlinear Schr?dinger equation，satisfied by large amplitude Rossby envelope solitary waves in shear basic flow with beta effect，is derived.The effects of basic flow shear and beta effect on the nonlinear equatorial Rossby waves are also analyzed.

equatorial Rossby wave，β effect，nonlinear Schr?dinger equation，envelope soliton

*內蒙古自然科學重點基金(批準號:2009ZD01)和內蒙古教育廳基金(批準號:NJZY08005)資助的課題.?通訊聯系人.E-mail:lgyang@imu.edu.cn

*Project supported by the Natural Science Foundation of Inner Mongolia，China(Grant No.2009ZD01)and the Educational Department of Inner Mongolia，China(Grant No.NJZY08005).

?Corresponding author.E-mail:lgyang@imu.edu.cn