平面柔性梁的剛-柔耦合動力學特性分析與仿真*

和興鎖 李雪華 鄧峰巖

(西北工業大學工程力學系，西安 710072)

(2010年1月31日收到;2010年5月3日收到修改稿)

平面柔性梁的剛-柔耦合動力學特性分析與仿真*

和興鎖?李雪華 鄧峰巖

(西北工業大學工程力學系，西安 710072)

(2010年1月31日收到;2010年5月3日收到修改稿)

針對大范圍運動規律為未知的剛-柔耦合系統研究其動力學特性.利用有限元方法對柔性梁進行離散，采用Lagrange方程建立平面柔性梁的剛-柔耦合動力學方程，研究在大范圍運動為自由情況下，平面柔性梁的大范圍運動和變形運動的相互耦合機理，比較零次模型、一次耦合模型及精確模型的差異，探討各種模型的適用性.

平面柔性梁，剛-柔耦合系統，動力學特性，分析與仿真

PACS:45.10.－ b，05.45.－ a，45.05.+x

1.引 言

文獻［1，2］針對非慣性坐標系下大范圍運動規律為已知的柔性梁結構進行了研究，在這類研究中，剛體運動是作為已知運動出現的，表征剛體運動的坐標并不出現在系統的動力學方程中，因此實際上這類剛-柔耦合動力學研究的是單向問題，即只考慮了大范圍運動對柔性結構的影響，而未考慮柔性體的變形對剛體運動的影響.但在工程實際中，剛體運動規律未知的剛-柔耦合結構也大量存在于實際機構中，如給定驅動力矩的柔性機械臂等結構.因此這類考慮剛-柔部件之間相互耦合作用的動力學問題也受到研究者越來越多的重視［3—5］.同時，對中心剛體-卷簧-柔性梁這類典型結構，有研究者也進行了一些理論和實驗研究［6—8］.以往的研究在一定程度上為工程實際應用做好了理論準備［9，10］.

但以往的研究未考慮完全的幾何非線性變形模式，其動力學方程及實驗比較是建立在一次耦合模型基礎上的，因此只探討了零次模型和一次耦合模型的差異，以及耦合模型與剛體模型之間的差異，并未探討耦合模型之間的差異.本文將對這些問題進行深入的研究.

2.平面柔性梁的剛-柔耦合動力學特性分析

圖1所示為一固結在旋轉中心剛體上的平面懸臂柔性梁，中心體半徑為 R，轉角為 θ，角速度為 θ·，角加速度為θ¨，中心剛體的轉動慣量為 J0，中心剛體與機架之間裝有剛度為K0的扭轉彈簧，該模型為研究剛-柔耦合動力學問題的典型模型.

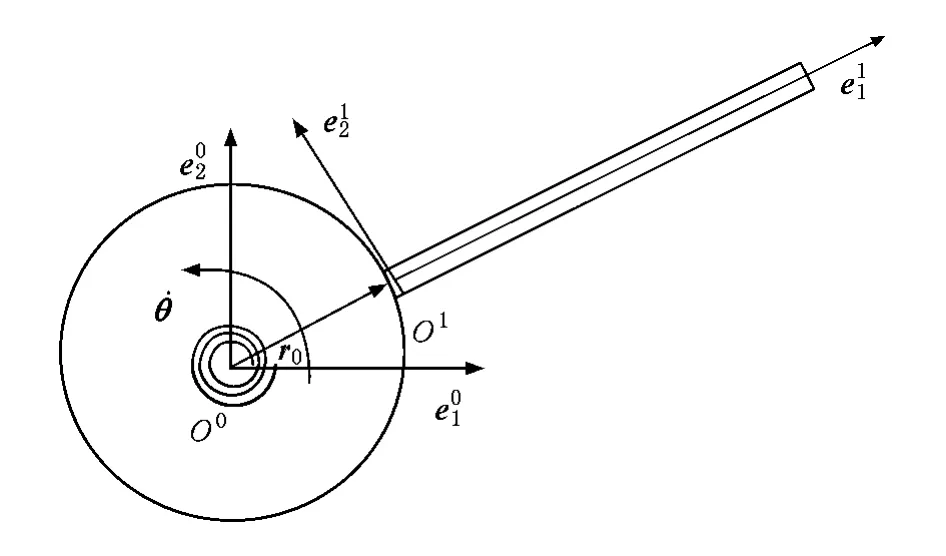
圖1 由中心剛體-柔性梁-扭簧組成的剛-柔耦合系統

對于大范圍運動規律未知，系統廣義坐標為

式中qf表示節點的位移.中心剛體動能和扭轉彈簧勢能分別為

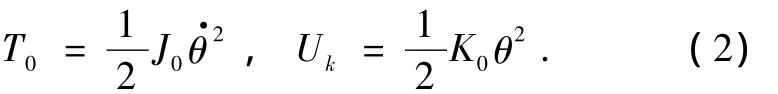
不計分布外力，利用有限元離散后，采用 Lagrange方程可得剛-柔耦合系統的動力學方程為

式中的廣義質量陣M和廣義力陣Q分別為

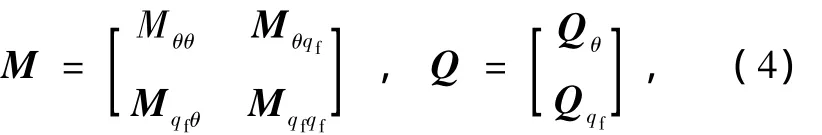
廣義質量陣M和廣義力陣Q 中的各參量分別為

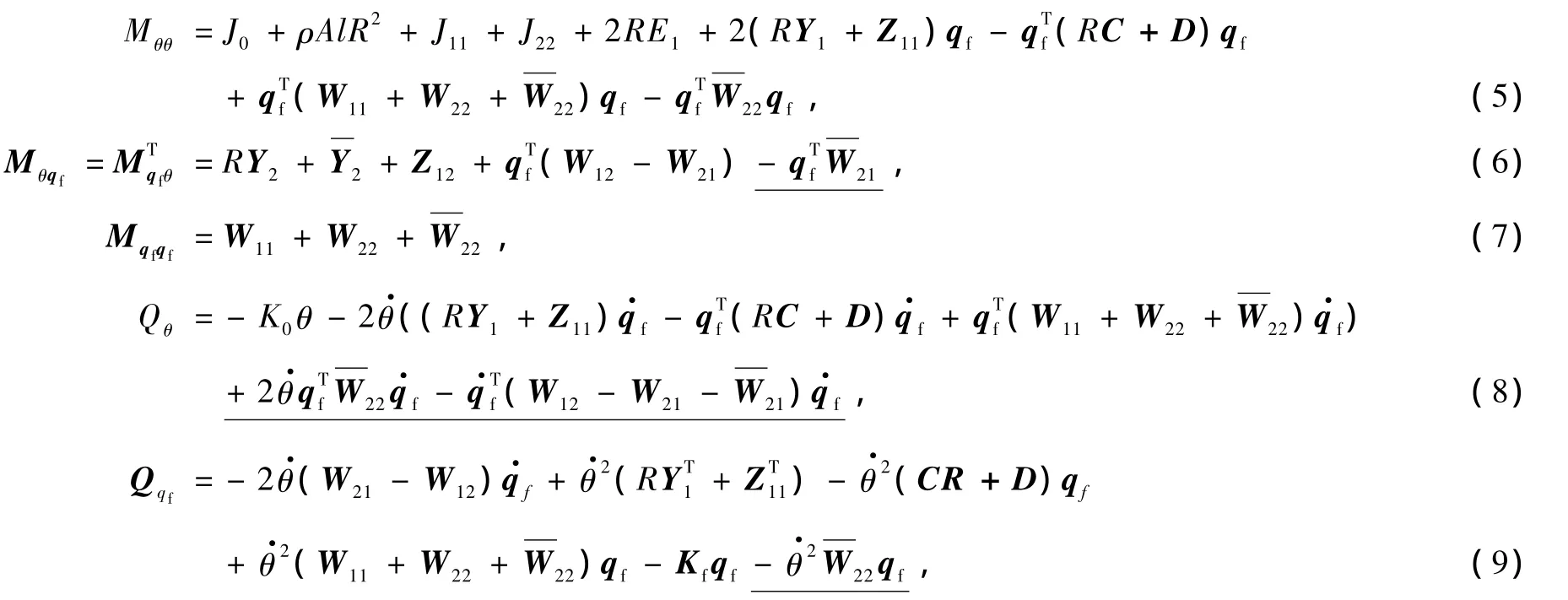
式中J0為中心剛體轉動慣量，A和l分別為梁的橫截面積和長度，ρ為密度，E為彈性模量.ρlIyy，Iyy和Izz為橫截面的慣性矩.K0為卷簧剛度，Kf為彈性梁固有彈性剛度陣.Y，Z，W，C，D等表示式見文獻［5］.

本文精確模型與一次耦合模型相比，增加了變形耦合項，即上述各式中的劃線項.另外，一次耦合模型和本文精確模型比零次耦合模型均增加了耦合項C和D.

現取梁的物理參數為:中心剛體半徑為 R=1 m，長度為l=8 m，彈性模量為 E=6.8952×1010N/m2，密度為 ρ=2.766×103kg/m3，橫截面積為 A=7.2986×10－5m2，橫截面慣性矩為 IZZ=8.2189×10－9m4.

1)當端點無初始變形，初始角度 θ(0)=0.01 rad，初始角速度(0)=0 rad/s，中心剛體轉動慣量 J0=30 kg·m2時，改變卷簧剛度 K0.零次模型、一次耦合模型和本文精確模型的計算仿真結果如圖2所示.

由圖2可知，當 K0=200 N·m/rad時，三種模型的仿真結果幾乎沒有差別.

根據文獻［7］，第一階頻率為扭轉彈簧產生的中心剛體大范圍運動的振動頻率，第二階頻率為柔性梁振動產生的一階頻率.三種模型下，第一、二階頻率幾乎無差別，均為0.2188和0.7813 Hz.增加卷簧剛度至K0=1000 N·m/rad，計算仿真結果如圖3所示.

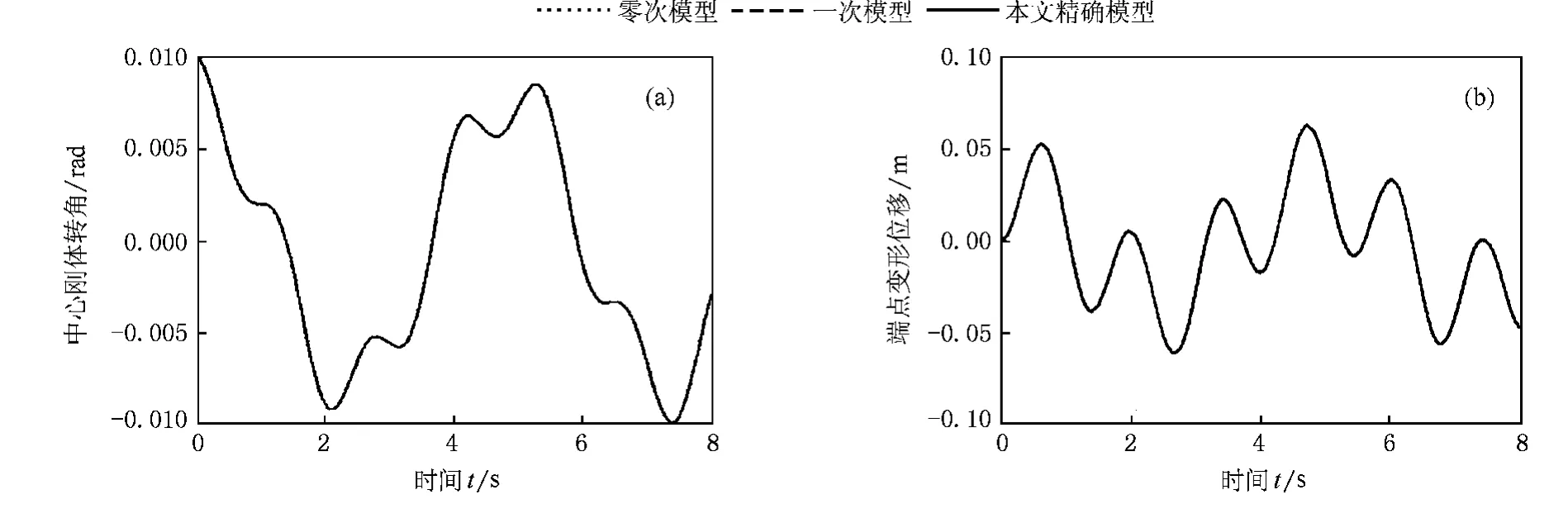
圖2 K0=200 N·m/rad，J0=30 kg·m2，θ(0)=0.01 rad時，中心體轉角以及梁端點在 方向的變形位移 (a)中心剛體轉角，(b)端點變形位移

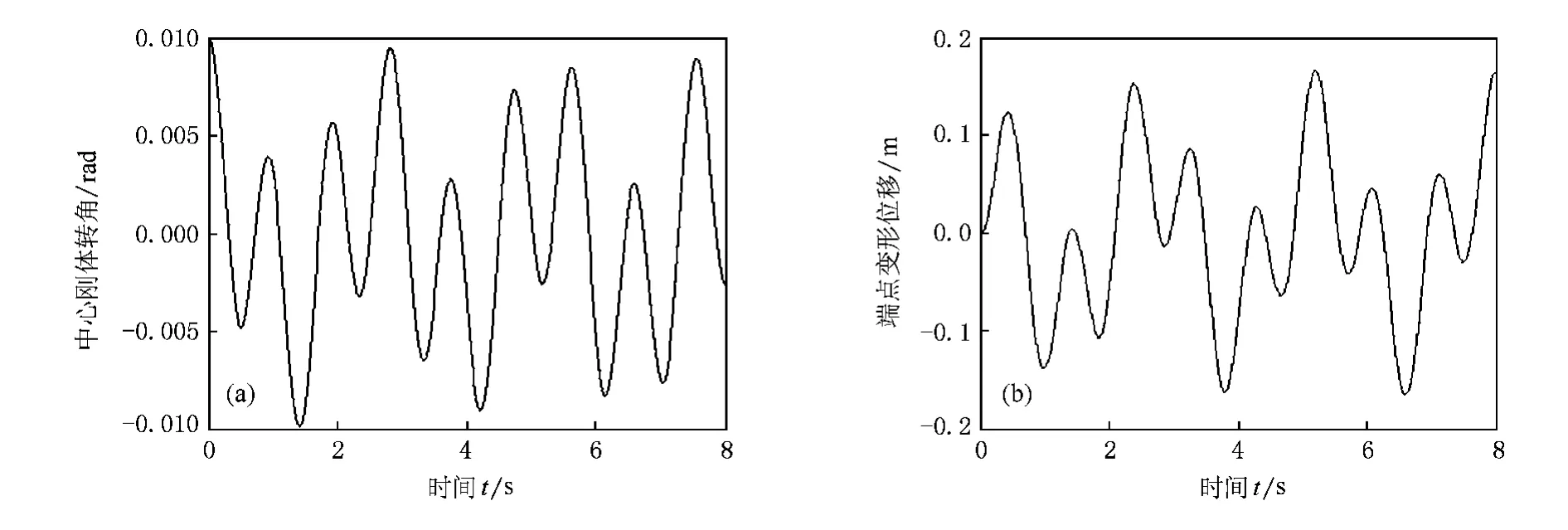
圖3 K0=1000 N·m/rad，J0=30 kg·m2，θ(0)=0.01 rad時，中心體轉角以及梁端點在 e12方向的變形位移 (a)中心剛體轉角，(b)端點變形位移

由圖3曲線可見，即便加大彈簧剛度，三種模型的轉角響應、端點位移響應幾乎沒有差別.計算仿真結果同時表明，三種模型的第一、第二階頻率都變大，但幾乎沒有差別，依次為0.375和1.0625 Hz.因此在初始角較小的情況下，剛-柔剛度比［7］Kp=K0l/EIzz，對三種模型幾乎沒有影響.

2)當端點無初始變形，初始角度 θ(0)=0.01 rad，初始角速度(0)=0 rad/s，卷簧剛度 K0=200 N·m/rad，中心剛體轉動慣量 J0=3 kg·m2時，計算仿真結果如圖4所示.由圖示曲線可見，減小中心剛體轉動慣量，對三種模型的轉角響應和端點位移響應幾乎沒有差別.三種模型的第一、二階頻率都比相同剛度下變大，但它們之間幾乎沒有差別，依次為0.25和1.5313 Hz.因此在初始角較小的情況下，剛柔慣量比［7］Jp=J0/Jb，對三種模型幾乎沒有影響.其中 Jb=ρAl3/12+ρAl(0.5+R)2為梁未變形時，相對于中心轉軸的轉動慣量.此外由于中心體轉動慣量的減小，柔性梁的高階頻率(第三階頻率)被激發出來，但其對中心剛體和柔性梁的振動貢獻較小.

計算與仿真結果表明，本文精確模型與一次耦合模型差異不明顯，說明對于平面剛-柔耦合系統，在基點運動速度和中心剛體大范圍運動都較小的情況下，新增的變形耦合項作用較弱.隨著卷簧剛度的增加和中心體轉動慣量的減小，中心體的轉角和梁的端點位移振動幅值變大且波動加劇.

中心剛體初始轉角增加后，一次耦合模型和本文精確模型的端點位移響應、轉角響應以及頻率幾乎沒有差別，但這兩種模型與零次模型的差別變得明顯.本文精確模型與一次耦合模型的第一階頻率為0.2344 Hz，而零次耦合模型第一階頻率為0.2266 Hz;本文精確模型與一次耦合模型的第二階頻率為0.8125 Hz，而零次耦合模型第二階頻率為0.7188 Hz.觀察中心剛體的角速度響應，如圖6所示.

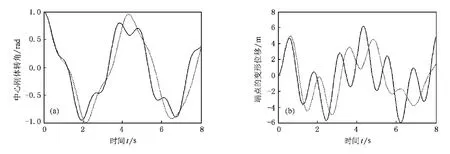
圖5 K0=200 N·m/rad，J0=30 kg·m2，θ(0)=1 rad時，中心體轉角以及梁端點在方向的變形位移 (a)中心剛體轉角，(b)端點變形位移

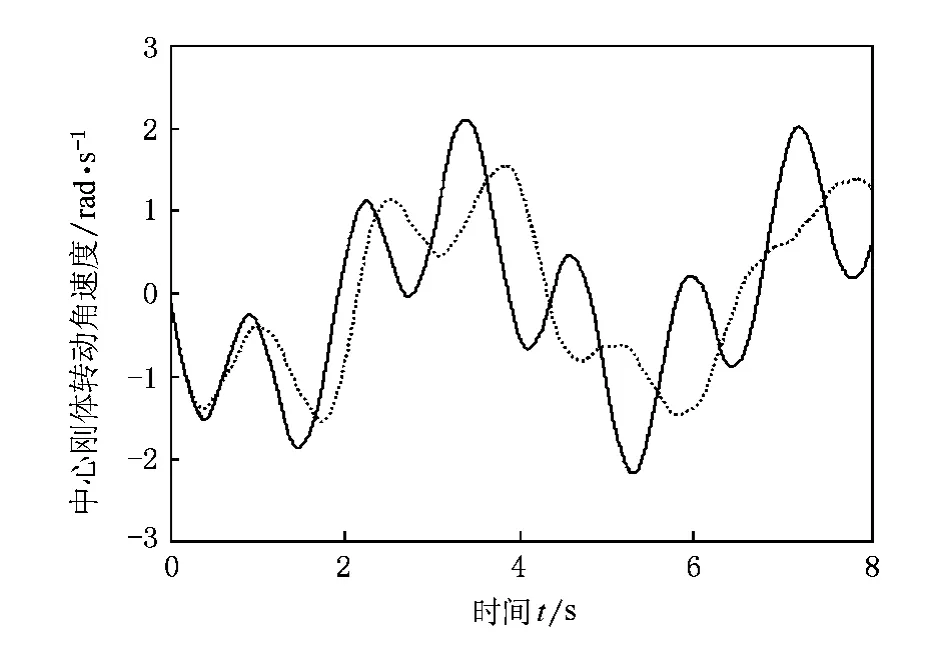
圖 6 K0=200 N·m/rad，J0=30 kg·m2，θ(0)=1 rad 時，中心剛體轉動角速度

初始角度變大后，中心體轉速較高，中心體運動范圍也變大，角速度峰值接近2 rad/s，可見在角速度較大情況下，耦合項C，D作用明顯，使得柔性梁產生動力剛化現象，對應剛-柔耦合的中心剛體-柔性梁結構，即第二階頻率增加;對于中心剛體的振動頻率(第一階頻率)而言，耦合項 C，D也起到一定的作用.

改變K0和R以獲得不同剛柔剛度比Kp和剛柔慣量比Jp，比較不同初始角下的第一、二階頻率，如表1和表2所示.表中，一次耦合模型和本文精確模型統稱為耦合模型.

3.算例結果分析

在相同剛柔剛度比或剛柔慣量比的情況下，當初始角較大時，角速度變化增大，中心體運動范圍變大，零次模型和耦合模型的第一、二階頻率呈現差異.第二階頻率對應為柔性梁的振動頻率，與零次模型相比，由于C，D項的作用，耦合模型產生了動力剛化現象，隨著初始角的增加，該階頻率逐漸變大，而零次模型的該階頻率逐漸變小.此外，第一階頻率為扭轉彈簧產生的中心剛體大范圍運動的振動頻率，零次模型的該階頻率保持不變，耦合模型的該階頻率在初始角較大情況下會升高.相對于第二階頻率，耦合模型的第一階頻率只有在初始角較大的情況下，如表1中初始角為1 rad時才會有所提高，而第二階頻率在相同剛柔剛度比或剛柔慣量比的情況下，具有較小的初始角就會有所提高，如表1中初始角為0.5 rad時.這說明耦合模型下能夠反映大范圍運動對剛體振動的影響，同時柔性梁的振動受系統的大范圍影響較大，在柔性梁振動為主的情況下，耦合模型的動力剛化現象較明顯.

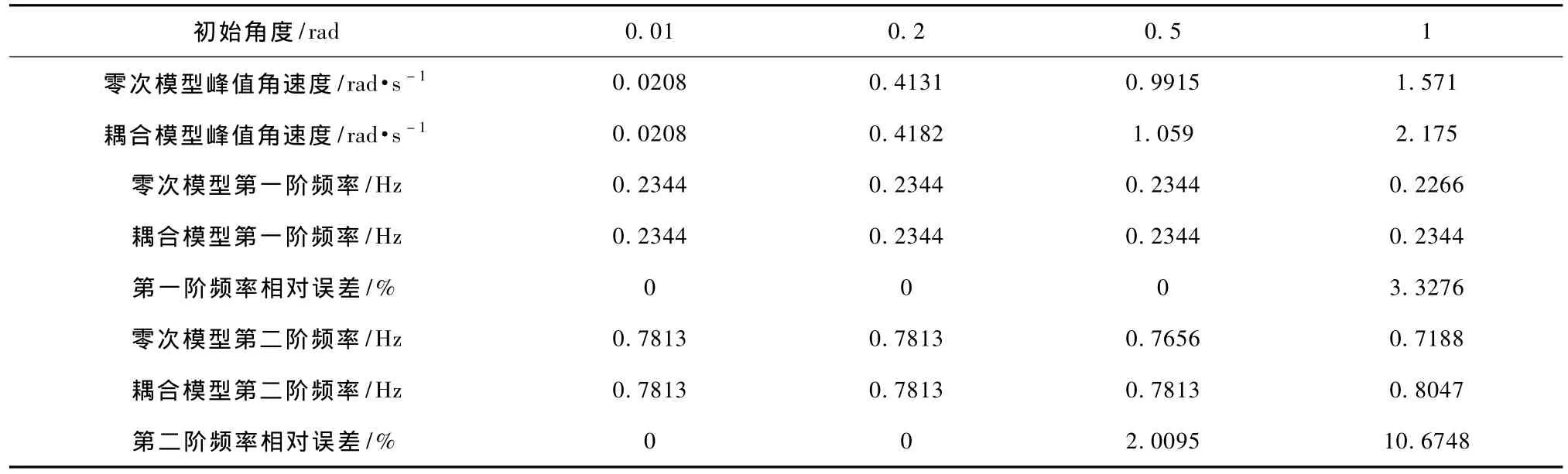
表1 Kp=K0l/EIzz=2.82332，Jp=J0/Jb=0.612378時，初始角對系統頻率的影響

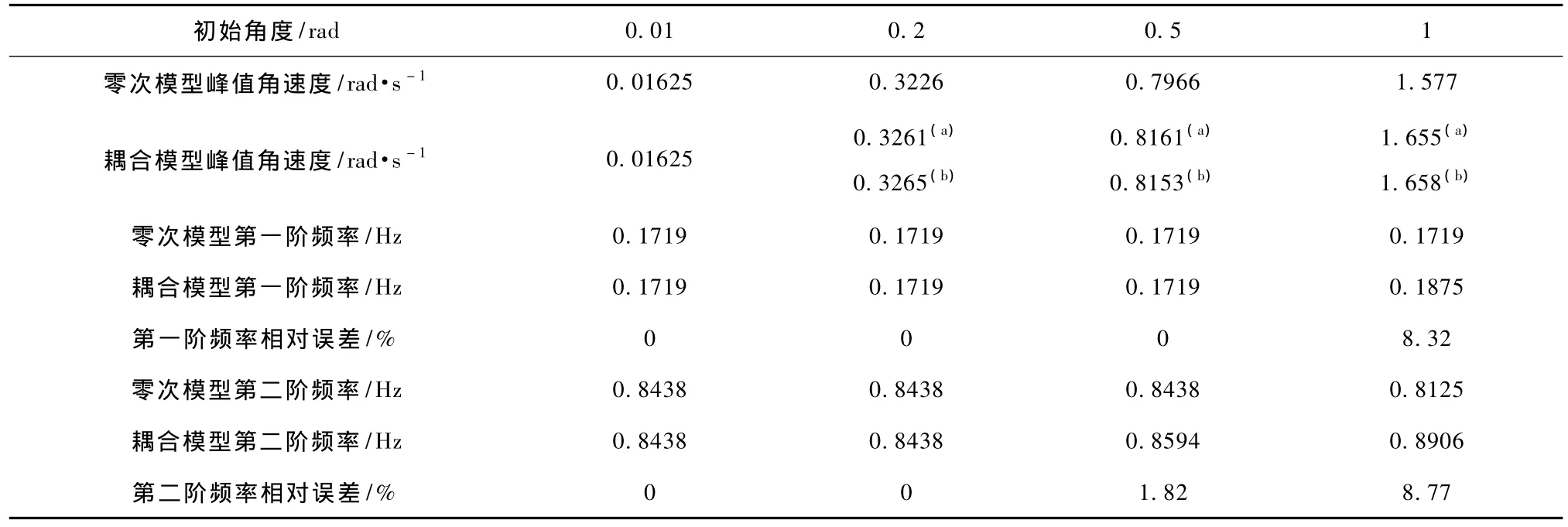
表2 Kp=K0l/EIzz=2.82332，Jp=J0/Jb=0.267915時，初始角對系統頻率的影響

在初始角增幅較小的情況下，角速度變化較小，中心體運動范圍較小，若此時剛柔剛度比較大或剛柔慣量比較小，耦合模型的第二階頻率仍會較零次模型變大，如表2在初始角為0.2 rad時，兩種模型就呈現了差異，這也說明柔性梁的頻率受系統運動的影響較大.

對于轉角、端點位移以及頻率響應，無論初始角度如何，即無論剛體運動范圍是否變大，一次耦合模型與本文精確模型差別很小，說明對于大范圍運動為未知的平面剛-柔耦合結構而言，變形的相互耦合作用以及基點速度和角速度的耦合作用并不明顯，這不同于非慣性系下大范圍運動為已知的平面剛-柔耦合結構.

4.結 論

本文對大范圍運動規律為未知的中心剛體-柔性梁-扭簧這一典型的剛-柔耦合結構進行了研究.與零次模型和一次耦合模型相比，本文精確模型下動力學方程包含了完整的耦合項.

研究發現，在初始角度較大，即系統具有較大的運動速度和大范圍剛體運動時，零次模型與一次耦合模型和本文精確模型會出現差異，一次耦合模型和本文精確模型能夠體現出動力剛化效應，其高階頻率會隨著大范圍運動的增加而上升，而零次模型則相反.對于平面剛-柔耦合結構，一次耦合模型與本文精確模型的仿真結果差異不大，說明新增的變形耦合項作用不明顯.因此對于大范圍運動為未知的剛柔耦合結構，其大范圍運動的速度和幅度依然是決定動力學特性和動力學模型適用的重要因素.在非慣性系下的動力剛化效應，也存在于運動規律未知的剛-柔耦合結構中.

［1］He X S，Deng F Y 2010Acta Phys.Sin.59 25(in Chinese)［和興鎖、鄧峰巖2010物理學報 59 25］

［2］Deng F Y，He X S，Li L，Zhang J 2007Multibody Syst.Dyn.18 559

［3］Liu Y Z 2009Chin.Phys.B 18 1

［4］Meng Z，Liu B 2008Acta Phys.Sin.57 1329(in Chinese)［孟 宗、劉 彬2008物理學報57 1329］

［5］He X S，Deng F Y，Wang R 2010Acta Phys.Sin.59 1434(in Chinese)［和興鎖、鄧峰巖、王 容 2010物理學報 59 1428］

［6］Fu J L，Chen B Y，Tang Y F，Fu H 2008Chin.Phys.B 17 3942

［7］Yang H 2002Ph.D.Dissertation(Shanghai:Shanghai Jiao Tong University)(in Chinese)［楊 輝 2002博士學位論文(上海:上海交通大學)］

［8］Liu J Y 2000 Ph.D.Dissertation(Shanghai:Shanghai Jiao Tong University)(in Chinese)［劉錦陽2000博士學位論文(上海:上海交通大學)］

［9］Xue Y，Weng D W 2009 Acta Phys.Sin.58 34(in Chinese)［薛 紜、翁德瑋 2009物理學報 58 34］

［10］Bai C L，Zhang X，Zhang L H 2009 Chin.Phys.B 18 475

PACS:45.10.－ b，05.45.－ a，45.05.+x

Analysis and imitation of dynamic properties for rigid-flexible coupling systems of a planar flexible beam*

He Xing-Suo?Li Xue-Hua Deng Feng-Yan

(Department of Engineering Mechanics，Northwestern Polytechnical University，Xi'an 710072，China)

(Received 31 January 2010;revised manuscript received 3 May 2010)

The finite element method is used for the system discretization and the coupling dynamic equations of flexible beam are obtained by Lagrange's equations.The second order coupling terms between rigid large overall motion，arc length stretch，lateral flexible deformation kinematics and torsional deformation terms are included in the present exact coupling model to expand the theory of one-order coupling model.The dynamic response of the present model is compared with that of zero-order approximate model and one-order coupling model.Then the changes of dynamic stiffening terms due to the new coupling terms are discussed according to different models.At the same time，the effect of initial static deformation in the tip is considered to study the vibrant deformation of flexible beam.The difference between zero-order approximate model，one-order coupling model and the present exact model is revealed by the frequency spectrum analysis method and it is concluded that the speed of overall motion is a vital cause for the difference between different models.And we found that the dynamic stiffening phenomenon still exists in rigid-flexible coupling system while the overall motion is free.But the effect of dynamic stiffening in the present exact model is not as severe as that in the one-order coupling model.

planar flexible beam，rigid-flexible coupling systems，dynamic properties，analysis and imitation

*國家自然科學基金(批準號:10672133)資助的課題.

*Project supported by the National Natural Science Foundation of China(Grant No.10672133).