狀態轉換行業系統性風險與市場波動關聯性
——基于深圳股市的實證研究

陳曉紅 ,岳 崴,曹 裕

(中南大學商學院,湖南長沙 410083)

狀態轉換行業系統性風險與市場波動關聯性
——基于深圳股市的實證研究

陳曉紅 ,岳 崴,曹 裕

(中南大學商學院,湖南長沙 410083)

以 2002-2009年深圳股市市場指數和 22個行業指數為研究樣本,本文運用不同的一階馬爾可夫過程刻畫市場波動與行業系統性風險的狀態轉換行為,在此基礎上估計了不同市場波動狀態下行業系統性風險處于不同狀態的條件概率,然后基于估計的條件概率探討了行業系統性風險狀態與市場波動狀態之間的關聯性。實證結果表明：市場波動和行業系統性風險均存在明顯的兩狀態轉換行為;其中采掘業等八個行業組合的系統性風險狀態與市場波動狀態之間存在正向的關聯性;制造業等八個行業組合的系統性風險狀態與市場波動狀態之間存在反向的關聯性;其他行業組合的系統性風險狀態與市場波動狀態之間不存在明顯的關聯性。可以利用行業系統性風險狀態與市場波動狀態之間的關聯特性并根據市場波動狀態的變化動態調整投資組合。

馬爾可夫狀態轉換;市場波動;行業系統性風險;狀態關聯性

一、引言

源自資本資產定價模型 (CAPM)的β系數是測度證券系統性風險的主要指標,它刻畫了證券(組合)收益率對市場風險溢價變化的敏感程度。一系列實證研究發現,不同行業證券組合的系統性風險 (由β系數所測度)對市場波動變化的反應可能不同。Brooks,Faff和 McKenzie(1998)[1]使用Schwert和 Seguin(1990)[2]的異方差市場模型①Schwert和 Seguin(1990)[2]提出異方差市場模型 (heteroskedastic market model)以考察β系數的時變特征：rit=ai+βirmt+δi(rmt/σ2m t)+εit,時變的β系數由βssit=βi+δi/σ2mt所刻畫。σ2mt是市場組合的條件方差。正 (負)的系數δ1表示證券的β系數與整個市場波動之間具有負(正)相關關系。考察澳大利亞股市波動的變化對不同行業組合β系數的影響。發現一些行業組合的系統性風險隨著市場波動的加劇而增大,而一些行業組合的系統性風險隨著市場波動的加劇而減小。Episcopos(1996)[3]采用同樣的方法發現加拿大股票市場中 3個行業指數的系統性風險與市場指數的波動性正相關。投資組合的構建不僅要考慮各類資產的收益率及其收益率的波動性,而且還要考慮各類資產與整體資本市場的相關性。研究不同行業組合的系統性風險與市場波動變化的關系有助于投資者根據市場態勢的變化及時調整投資組合,對投資組合管理有積極的意義。

筆者認為,近來有關證券組合的系統性風險與市場波動變化關系的研究可能存在以下兩方面的不足：

第一,在對市場組合時變的波動率建模時,忽略了市場波動可能存在的結構性變化。具體來說,使用基于 Schwert和 Seguin(1990)[2]的方法考察市場波動的變化如何影響不同股票組合的β系數 (例如,Reyes(1999)[4],趙桂芹 (2003)[5]等 )大多通過 GARCH類模型獲得市場組合收益率的條件方差σm2

t。其隱含的假定是市場波動是連續和平滑變化的。然而,有關新興市場股市波動的研究發現,由于經濟政策非持續性和經濟結構的跳躍性變遷等原因使得其宏觀經濟表現出較強的不穩定性,這種不穩定性對投資者的預期可能產生很大的影響,這可能導致股市波動發生結構性的變化。因此,新興市場股市的波動可能存在狀態轉換行為。在這一意義上,Hamilton(1989)[6]提出的馬爾可夫狀態轉換模型 (Markov regime s witchingmodel)能更好地刻畫股市波動的階段性特征。使用馬爾可夫狀態轉換模型對市場組合收益率的波動變化過程建模,其基本思想是假定市場組合的收益率由不同的狀態產生,每個狀態具有不同的分布,而狀態為不可觀測的但服從一階馬爾可夫過程的隨機變量。與一些門限模型相比,馬爾可夫狀態轉換模型重要的區別在于變化的方式不是取決于過程的水平,而是取決于一種不可觀測的狀態變量。Ping Wang和 Mike Theobald(2008)[7]運用馬爾可夫狀態轉換模型研究了東亞六個新興市場其股市波動的變化過程,發現每個市場均存在明顯的波動狀態轉換行為。張兵 (2005)[8],高金余、陳翔 (2007)[9]等人也基于馬爾可夫狀態轉換模型給出了中國股市存在波動狀態轉換行為的實證證據。

第二,由于外部環境的沖擊會明顯影響證券(組合)收益率的分布,證券 (組合)的β系數也可能存在狀態轉換行為。Huang(2000)[10]假定證券的收益率是由高系統性風險和低系統性風險兩個狀態生成的,構建了基于馬爾可夫狀態轉換過程的 CAPM。蘇濤、詹原瑞、劉家鵬 (2007)[11],趙鵬、唐齊鳴 (2008)[12]利用馬爾可夫狀態轉換 CAPM估計了個股或者行業組合在不同狀態下的β系數,發現大多數證券 (組合)的β系數存在明顯的狀態轉換行為。

目前,同時考慮市場波動與行業 (或單個證券)β狀態轉換的研究還很少。Sascha Mergner和Jan Bulla(2008)[13]對歐洲行業組合的研究中,假定市場波動和行業系統性風險的狀態轉換服從相同的一階馬爾可夫過程。由于存在行業與經濟周期的非一致變化,假設市場波動和行業β同步變化可能與觀測到的經濟事實不一致。Galagedera和Shami(2004)[14]對美國股市的研究中,使用不同的一階馬爾可夫過程擬合市場波動和單個證券β系數的變動,估計了個股系統性風險狀態與市場波動狀態的聯合分布。

本文的目的是探討當市場波動與行業系統性風險同時存在狀態轉換行為時,這兩者狀態轉換行為之間的關聯性。在假定我國股市市場波動的狀態轉換行為和行業系統性風險的狀態轉換行為分別服從不同的一階馬爾可夫過程的基礎上,與Galagedera和 Shami(2004)[14]的研究不同,本文估計了不同市場波動狀態下行業系統性風險狀態的條件分布,并將行業系統性風險處于不同狀態下的條件概率作為行業系統性風險狀態與市場波動狀態之間關聯性的測度。具體的研究思路如下：首先,采用兩狀態的馬爾可夫狀態轉換模型分別對市場組合的波動狀態轉換過程和行業組合的系統性風險狀態轉換過程建模,然后獲得每個時刻市場組合處于高波動狀態和低波動狀態以及行業組合處于高系統性風險狀態和低系統性風險狀態的概率估計,并利用估計的狀態概率作為門限參數將樣本劃分至不同的狀態空間。接下來,通過整個樣本期間的狀態分布信息,估計了在高、低市場波動狀態下行業系統性風險處于不同狀態的條件概率。最后,基于估計的條件概率探討了不同行業組合的系統性風險狀態與市場波動狀態之間的關聯性。由于投資者首先可以綜合利用資本市場和宏觀經濟等各方面的信息 (而不僅僅是市場風險溢價)對當前市場所處的波動狀態進行推斷,在確定了市場波動狀態之后根據行業系統性風險狀態的條件分布進行投資決策,這一過程更充分利用了市場信息。

二、研究設計

基于 Turner et al(1989)[15],Huang(2000)[10],Galagedera和 Shami(2004)[14],趙鵬、唐齊鳴(2008)[12]等人的研究,本文假定市場組合在高波動狀態與低波動狀態之間轉換,行業組合在高系統性風險狀態與低系統性風險狀態之間轉換。因此采用兩狀態的馬爾可夫狀態轉換模型分別刻畫市場波動和行業系統性風險的狀態轉換行為。這樣的假定使得每個狀態都代表明確的經濟含義,同時為了確保這一設定的合理性,本文在實證部分進行了相關的檢驗。

(一)市場波動狀態轉換模型

假定市場組合的收益率由兩個不同的波動狀態產生,不同狀態之間的轉換由不可觀測的狀態變量決定,這一狀態變量服從一階馬爾可夫過程。具體地：

其中,rmt是減去無風險利率后市場組合的超額收益率 ,μsmt和為不同狀態下市場組合收益率的均值和方差,μsmt和的取值均依賴于不可觀測的狀態變量是關于時間 t齊次且具有狀態空間 J=(1,2)的一階馬爾可夫過程,其轉移矩陣 P=(pij),其中 pij=P(smt=j|sm,t-1=i)i,j∈J且對任意 的大小刻畫了市場組合不同狀態下的波動特征。

rmt在不同狀態下的條件密度為：

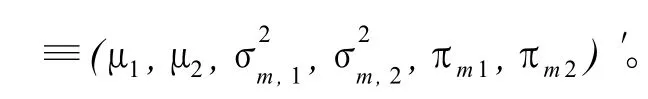
由上面的條件密度和無條件概率可以得到 rmt和 smt的聯合密度分布函數：

由于狀態變量 smt是無法觀測的,上式是描述實際觀測到 rmt的相對密度,若狀態變量 smt為跨時期 t的獨立同分布,則觀測到數據的對數似然值為：

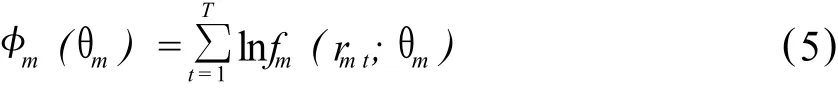
在限制πm1+πm2=1(πm1,πm2＞0)條件下最大化上式可得到θm的最大似然估計,Hamilton(1989)[6]提供了一個詳細的估計框架。

(二)狀態轉換資本資產定價模型

假定行業組合的收益率是由兩個狀態生成的,下述的兩狀態馬爾可夫狀態轉換 CAPM描述了各個行業組合收益率的生成過程：

類似于模型 (1),sit是具有狀態空間 K=(1,2)和轉移矩陣 P=(pij)的一階齊次馬爾可夫過程 ,pij=P(sit=j|si,t-1=i)i,j∈K,對任意pij=1。rit是第 i個行業組合的超額收益率,rmt是市場組合的超額收益率,βisit測度了第 i個行業組合在兩個狀態下的系統性風險,σis則刻畫了不同狀態it下行業組合的特有風險 (非系統性風險)。

類似于 (一)的分析,rit的無條件密度：

同樣,利用 Hamilton(1989)[6]的方法可以得到θi的最大似然估計。

(三)條件概率估計方法及狀態關聯性的定義

上文的波動狀態轉換模型和狀態轉換 CAPM分別刻畫了市場波動和行業組合系統性風險的狀態轉換行為,并且兩者的狀態轉換行為服從不同的一階馬爾可夫過程。本節的目的是首先估計條件概率 p(sit=k|smt=j),即在 t時刻市場處于波動狀態 j時,行業系統性風險處于狀態 k的條件概率。然后在條件概率的基礎上給出狀態關聯性的定義。

1.條件概率估計方法

雖然狀態變量 sit和 smt是無法觀測的,但我們可以根據 rmt和 rit的時間序列推斷出在 t時刻系統處于某一狀態的概率。Kim(1994)[16]建立的平滑算法可以獲得 t時刻市場波動或者行業系統性風險所處狀態的平滑概率,即基于全部觀測值信息所得到的 t時刻市場組合處于狀態 j的概率 P(smt=j)和行業系統性風險處于狀態 k的概率 P(sit=k)。為了方便說明,假設對模型 (1)和 (6)有σm,1＜σm,2,βi1＜βi2,即市場組合的狀態 1和狀態 2分別是低波動狀態和高波動狀態,行業組合的狀態 1和狀態 2分別是低系統性風險狀態和高系統性風險狀態。

如果 P(smt=1)＞P(smt=2)即 t時刻市場組合處于低波動狀態的平滑概率大于高波動狀態的平滑概率,認為 t時刻市場處于低波動狀態;反之,則認為 t時刻市場處于高波動狀態。類似的,對行業組合來說,如果 P(sit=1)＞P(sit=2)即 t時刻行業組合處于低系統性狀態的平滑概率大于高系統性風險狀態的平滑概率,則認為 t時刻行業組合處于低系統性風險狀態;反之,則認為 t時刻行業組合處于高系統性風險狀態。因為狀態概率是模型內生決定的,使用它作為劃分市場波動和行業系統性風險狀態的門限參數可以避免研究者主觀設定和選擇劃分標準的問題。

設 T為總觀測值個數,設第 i個行業組合滿足：

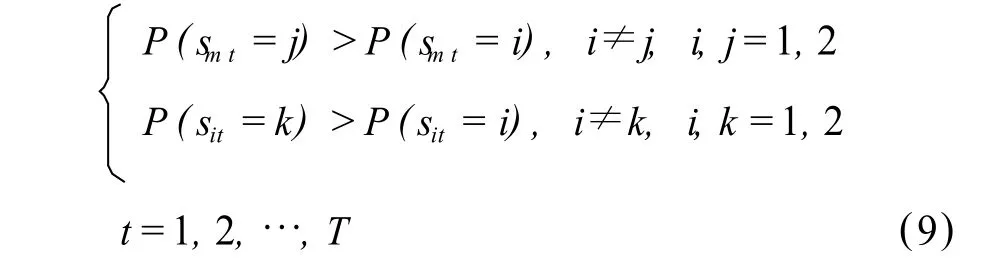
的觀測值個數為 Ti,jk,即同時處于市場波動狀態 j和系統性風險狀態 k的觀測值個數為 Ti,jk。因此,對行業組合 i,定義同時處于市場波動狀態 j和系統性風險狀態 k的無條件概率為：

Tm,j是市場組合處于波動狀態 j的觀測值個數,定義市場組合處于狀態 j的無條件概率為：

由條件概率公式可以計算在市場波動處于狀態 j時,第 i個行業組合的系統性風險處于狀態 k的條件概率：

按照上面的方法,可以估計下面四種條件概率：(1)給定市場處于低波動狀態 (low volatility regi me,LVR),行業組合處于低系統性風險狀態(low systematic risk regi me,LSRR)的條件概率 P(LSRR|LVR));(2)給定市場處于低波動狀態,行業組合處于高系統性風險狀態(high systematic risk regime,HSRR)的條件概率 P(HSRR|LVR));(3)給定市場處于高波動狀態 (high volatility regime,HVR),行業組合處于低系統性風險狀態的條件概率 P(LSRR|HVR));(4)給定市場處于高波動狀態,行業組合處于高系統性風險狀態的條件概率 P(HSRR|HVR))。

2.基于條件概率的狀態關聯性

本文探討的狀態關聯性是以上述條件概率測度行業系統性風險的狀態轉換行為與市場波動的狀態轉換行為兩者之間的一致性。具體地,我們定義：(1)對某個行業組合,如果 P(LSRR|LVR)＞P(HSRR|LVR)和 P(HSRR|HVR) ＞P(LSRR|HVR)同時成立,即當市場處于低 (高)波動狀態時,行業組合也以較高的概率處于低 (高)系統性風險狀態,則這個行業組合的系統性風險狀態與市場波動狀態之間存在正向的關聯性;(2)如果 P(HSRR|LVR)＞P(LSRR|LVR)和 P(LSRR|HVR)＞P(HSRR|HVR)同時成立,即當市場處于低 (高)波動狀態時,行業組合以較高的概率處于高 (低)系統性風險狀態,則這個行業組合的系統性風險狀態與市場波動狀態之間存在反向的關聯性。

估計上述條件概率和分析行業系統性風險狀態與市場波動狀態之間關聯性的意義在于,由于投資者可以綜合運用各種方法和各方面的信息(而不僅僅是市場收益率)首先對市場波動當前所處的狀態進行推斷①馬爾可夫狀態轉換模型本身提供對波動狀態的推斷,更多的討論見 Turner et al(1989)[15]等。,在確定了市場當前所處的波動狀態之后再根據行業系統性風險狀態在此市場波動狀態下的條件分布調整投資組合。這一過程將更多可用的信息納入投資決策中,更加充分利用了市場信息。

三、實證結果與分析

(一 )數據

本文選擇深圳股市 2002年 1月 1日到 2009年 12月 31日 22個行業指數的周收益率數據進行實證研究,市場組合選擇深證綜合指數,共 401組觀測值。無風險利率采用金融機構三個月定期存款基準利率。所有數據均來自W ind金融數據庫。

(二)市場波動狀態轉換模型估計結果與檢驗

Massimo Guidolin和Allan Timmermann(2008)[17]建議使用 Schwarz信息準則 (SIC)來確定馬爾可夫狀態轉換模型的最優狀態個數。表1列示了從兩狀態到六狀態一共 5種不同狀態數設定下的SIC,可以看出狀態數為 2時的 SIC最小 (為了節省篇幅,其他狀態數設定下的參數估計結果沒有列示在表中)。因此,兩狀態是模型最優的狀態數設定,先前關于市場波動轉換狀態的假定是合理的,假定市場組合在兩個波動狀態之間轉換很好地描述了波動的階段性特征。

表1 波動狀態轉換模型估計結果

為了進一步檢驗模型設定是否合理,本文采用 Krozig(1997)[18]建議的 Davies檢驗來檢驗模型在兩個狀態下的參數是否存在顯著的差別。檢驗的原假設和備擇假設分別為：

表1中 Davies檢驗的 P值顯示,市場組合在1%的水平上拒絕了原假設,說明兩個狀態存在顯著的區別,模型沒有被誤設。由模型的參數估計結果,可以看出σm,2為σm,1的 2倍以上,說明市場組合在兩個狀態下的波動特征存在明顯的差異,可以認為市場組合的收益率是由低波動狀態 (狀態 1)和高波動狀態 (狀態 2)兩個狀態產生的。兩個狀態的持續概率 p11、p22為 0.98和 0.97,說明這兩個狀態都是比較穩定的。低波動狀態的期望持續期為 52.04周,而高波動狀態的期望持續期為 33.58周,低波動狀態的期望持續期要大于高波動狀態。圖1、圖2給出了兩個波動狀態的平滑概率。

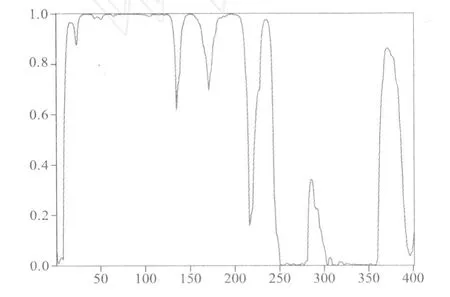
圖1低波動狀態平滑概率

圖2 高波動狀態平滑概率

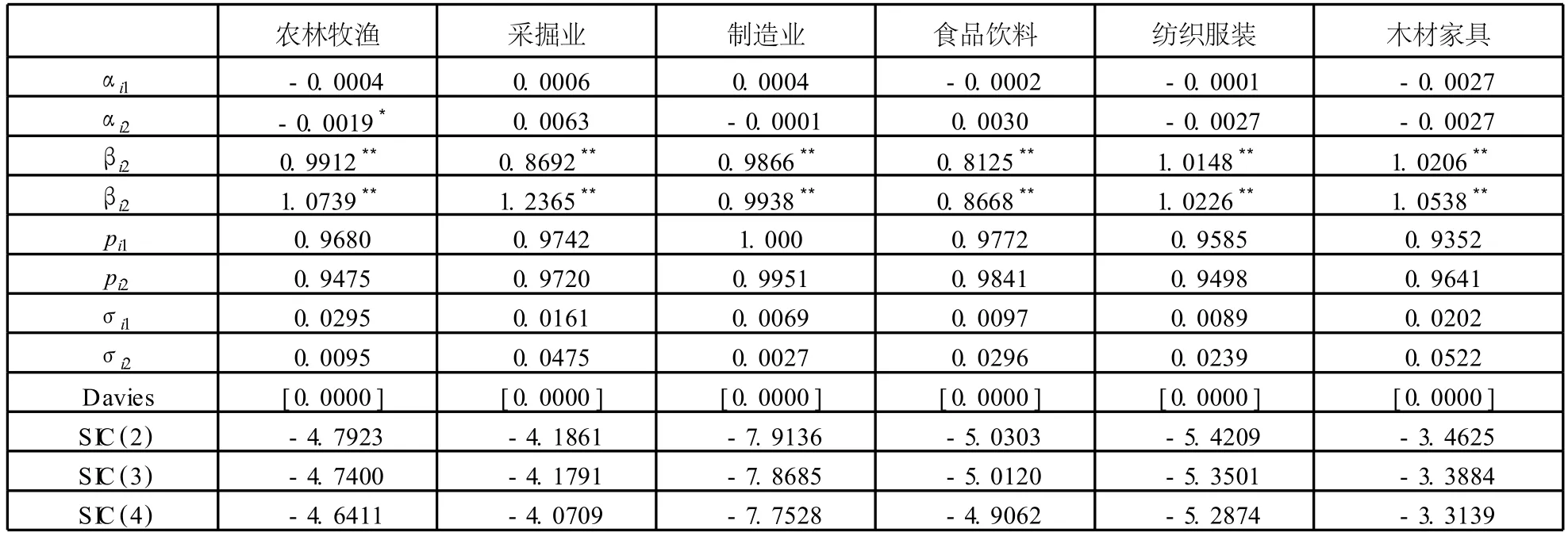
表2 狀態轉換 CAPM估計結果

(三)狀態轉換 CAPM估計結果與檢驗

表2給出了 22個行業組合狀態轉換 CAPM模型的估計結果。比較不同狀態數下模型的 SIC,我們發現對所有的 22個行業組合來說,在兩狀態設定下模型的 SIC最小,因此狀態轉換 CAPM的最優狀態設定是兩狀態,我們先前的假定是合理的。類似于 (一),這里同樣使用 Davies檢驗來檢驗狀態轉換 CAPM在兩個狀態下的參數是否存在顯著的差別,檢驗的原假設和備擇假設分別為：

表2中 Davies列示了 Davies檢驗的 P值,我們可以看出,所有 22個行業組合均在 1%的水平上拒絕了原假設,說明兩個狀態存在顯著的差異,模型沒有被誤設。截距項αi1和αi2是狀態轉換CAPM在兩種狀態下的定價誤差,若αi1或αi2顯著不為零則說明模型遺漏了影響行業組合收益率的其他重要因素。22個行業組合的αi1和αi2的估計結果顯示,除了農林牧漁組合的αi2和金融保險的αi1值顯著不為零外,其他 42個定價誤差的估計值均不顯著異于零,說明我們采用兩狀態的狀態轉換 CAPM能夠解釋絕大多數行業收益率的變化,而沒有遺漏影響資產收益率的其他重要因素。對22行業組合來說,有βi1＜βi2,因此可以認為狀態 1是低系統性風險狀態,狀態 2是高系統性風險狀態,行業組合的收益率是由這兩個狀態生成的。上述結果與趙鵬、唐齊鳴 (2008)[12]利用 1997-2007年數據所得出的結果基本一致,即我國行業證券組合的β系數存在明顯的狀態轉換行為。

續表2

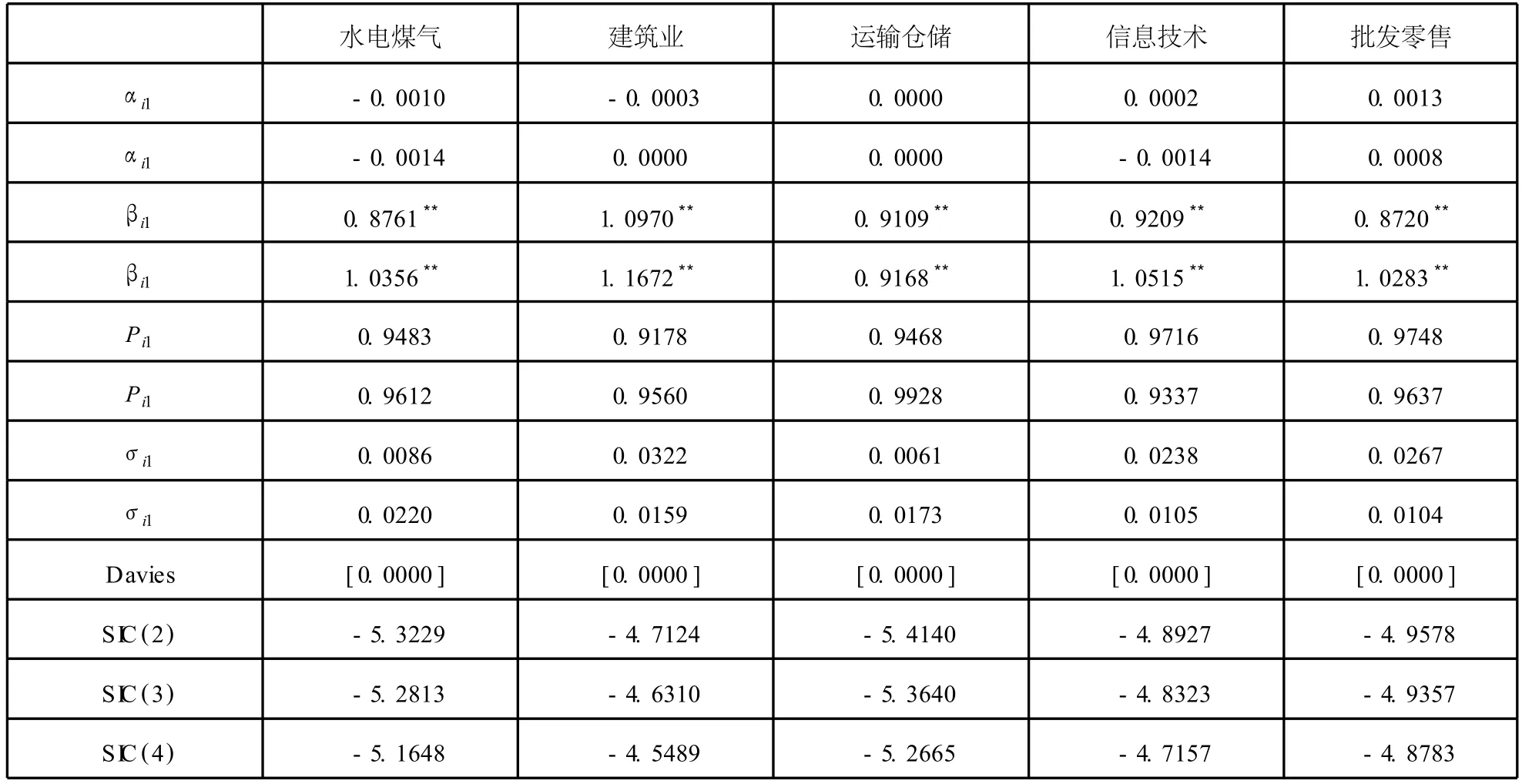
續表2

續表2

(四)條件概率估計結果與狀態關聯性分析

根據市場波動狀態和行業系統性風險狀態的平滑概率①由于篇幅的限制,這里沒有給出 22個行業組合其系統風險狀態的平滑概率,需要的讀者可以和作者聯系。,按照上文所述的方法,對 22個行業組合估計了 P(LSRR|LVR)、P(HSRR|LVR)、P(LSRR|HVR)和 P(HSRR|HVR)四種條件概率。當市場波動和行業系統性風險同時存在狀態轉換行為時,該條件概率測度了這兩者狀態轉換行為之間的一致性。根據條件概率的估計結果 (見表3)和上文對狀態關聯性的定義,我們發現：

(1)對采掘業、食品飲料、紡織服裝、造紙印刷、機械設備、水電煤氣、社會服務、綜合類八個行業,P(LSRR|LVR)＞P(HSRR|LVR)和 P(HSRR|HVR)＞P(LSRR|HVR)同時成立。說明當市場處于高波動狀態時,上述行業組合以較高的概率處于高系統性風險狀態;當市場處于低波動狀態時,上述行業組合也以較高的概率處于低系統性風險狀態。這八個行業組合的系統性風險狀態轉換行為與市場波動狀態轉換行為之間存在正向的關聯性。

(2)對制造業、石化塑膠、電子、醫藥生物、建筑業、批發零售、房地產、傳播文化八個行業,P(HSRR|LVR)＞P(LSRR|LVR)和 P(LSRR|HVR)＞P(HSRR|HVR)同時成立。說明當市場處于低波動狀態時,上述行業組合以較高的概率處于高系統性風險狀態;當市場處于高波動狀態時,上述行業組合以較高的概率處于低系統性風險狀態。與前面的八個行業組合的情況相反,這八個行業組合的系統性風險狀態轉換行為與市場波動狀態轉換行為之間存在反向的關聯性。

(3)無論市場處于高波動狀態還是低波動狀態,信息技術和金融保險這兩個行業組合總是以較高的概率處于低系統性風險狀態;木材家具、金屬非金屬和運輸倉儲這三個行業組合總是以較高的概率處于高系統性風險狀態。上述五個行業組合以及農林牧漁行業的系統性風險狀態轉換行為與市場波動狀態轉換行為之間的關聯性不明顯。

表3 條件概率估計結果

四、結論

本文探討了市場波動狀態轉換行為和行業系統性風險狀態轉換行為之間的關聯性。首先假定市場波動的狀態轉換過程和行業系統性風險的狀態轉換過程分別服從不同的一階馬爾可夫鏈。利用深圳股市的相關數據,我們發現在樣本期間,市場波動和行業系統性風險均存在明顯的狀態轉換行為：市場組合以一定概率在高波動狀態和低波動狀態之間轉換;22個行業組合也以一定的概率在高系統性風險狀態和低系統性風險狀態之間轉換。通過市場波動狀態和和行業系統性風險狀態的平滑概率劃分樣本所處的狀態空間,在此基礎上估計了：給定市場處于低 (高)波動狀態時,行業組合處于分別處于低系統性風險狀態與高系統性風險的條件概率;當市場波動和行業系統性風險同時存在狀態轉換行為時,狀態關聯性是以上述條件概率測度行業系統性風險與市場波動兩者狀態轉換行為之間的一致性。根據條件概率的估計結果,我們有以下基本結論：

(1)對采掘業、食品飲料、紡織服裝、造紙印刷、機械設備、水電煤氣、社會服務、綜合類八個行業板塊來說,其行業系統性風險狀態與市場波動狀態之間存在正向的關聯性。

(2)對制造業、石化塑膠、電子、醫藥生物、建筑業、批發零售、房地產、傳播文化八個行業板塊來說,其行業系統性風險狀態與市場波動狀態之間存在反向的關聯性。

(3)無論市場處于高波動狀態還是低波動狀態,信息技術和金融保險這兩個行業組合總是以較高的概率處于低系統性風險狀態;木材家具、金屬非金屬和運輸倉儲這三個行業組合總是以較高的概率處于高系統性風險狀態。上述五個行業組合以及農林牧漁行業的系統性風險狀態與市場波動狀態之間的關聯性不明顯。

由于投資者可以綜合利用資本市場和宏觀經濟等各方面的信息首先對市場所處的波動狀態進行推斷,因此依據不同市場波動狀態下行業系統性風險狀態的條件分布進行投資組合管理更充分利用了市場信息。而如何根據各方面的信息對市場波動狀態進行更準確的推斷,是我們下一步值得研究的問題。

[1]RobertD.Brooks,RobertW.Faff,MichaelD.McKenzie.Time Varying Beta Risk of Australian Industry Portfolios：A comparison of modeling Techniques[J].Australian Journal ofManagement.1998,23(1)：1-22.

[2]Schwert G W,Seguin P J.Heteroscedasticity in Stock Returns[J]. The Journal of Finance,1990,(4)：1129-1155.

[3]EpiscoposA.Stock Return Volatility and Time-varying Betas in the Toronto Stock Exchange[J].Quarterly Journal of Business and Economics,1996,(35)：28-38.

[4]Mario G.Reyes.Size,Time-varying Beta,and Conditional Heteroscedasticity in UK Stock Returns[J].Review of Financial Economics,1999,(8)：1-10.

[5]趙桂芹.股票收益波動與 Beta系數的時變性[J].中國管理科學,2003,11(1)：10-13.

[6]Hamilton J D.A new Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle[J].Econometrica,1989,57(2)：357-384.

[7]PingWang,Mike Theobald.Regime-switchingVolatility of Six EastAsian EmergingMarkets[J].Research in InternationalBusiness and Finance,2008,(22)：267-283.

[8]張兵.基于狀態轉換方法的中國股市波動研究[J].金融研究,2005,(3)：100-108.

[9]高金余,陳翔.馬爾可夫切換模型及其在中國股市中的應用[J].中國管理科學,2007,15(6)：20-25.

[10]Huang,H.-C.Tests of Regimes-s witching CAPM.Applied Financial Economics[J].2000,(10)：573-578.

[11]蘇濤,詹原瑞,劉家鵬.基于馬爾科夫狀態轉換下的CAPM實證研究[J].系統工程理論與實踐,2007,(6)：21-26.

[12]趙鵬,唐齊鳴.Markov區制轉換模型在行業 CAPM分析中的應用 [J].數量經濟技術經濟究,2008,(10)：87-97.

[13]SaschaMergner,Jan Bulla.Time-varyingBeta Risk of Pan-European Industry Portfolios：A Comparison of Alternative Modeling Techniques[J].The European Journal of Finance,2008,14(8)：771-802.

[14]Don U.A.Galagedera,Roland Shami.Association betweenMarkov Regi me-switching Market Volatility and Beta Risk：Evidence from Dow Jones Industrial Securities[J].2004,Finance 0406011,EconWPA.

[15]ChristopherM.Turner,Richard Startz,CharlesR.Nelson.A MarkovModel of Heteroskedasticity,Risk,and Learning in the StockMarket[J].Journal of Financial Economics,1989,25(1)：3-22.

[16]Chang-Jin Kim.Dynamic LinearModels with Markov-switching[J].Journal of Econometrics,1994,(60)：1-22.

[17]Massimo Guidolin,Allan Timmermann.Size and Value Anomalies underRegime Shifts[J].Journalof Financial Econometrics.2008,6(1)：1-48.

[18]Krolzig H M.Markov-Switching Vector Autoregressions Modelling,Statistical Inference and Application to Business Cycle Analysis[M].Berlin：Springer,1997.

(本文責編：潤 澤)

Association between Regi me-Switching Systematic Risk andMarket Volatility of Industry Portfolios:Empirical Evidence from Shenzhen StockMarket

CHEN Xiao-hong,YUEWei,CAO Yu
(School of Business,Central South University,Changsha410083,China)

This paper applies different first-orderMarkov process to model the regime-switching behavior of market volatility and systematic risk of industry portfolios based a sample of 22 industry stock indexes and market index of Shenzhen Stock Exchange,and further investigates the association between systematic risk regimes of industry portfolios and market volatility regimes.The empirical analysis results indicate that both market portfolio and industry portfolios have strong two-regime switching behavior.Through estimated conditionalprobabilitiesof systematic risk regimesof industry portfolios across differentmarket volatility regi mes,we find 8 industry portfolios display a positive association between systematic risk regimes and market volatility regimes and 8 industry portfolios display a negative association between systematic risk regimes and market volatility regi mes,and the rest industry portfolios display no significant association between systematic risk regimes and market volatility regimes.Dynamic portfolio management can be made based on association between systematic risk regimes and market volatility regi mes.

Markov regi me-s witching;market volatility;systematic risk of industry portfolios;regime-association

F830.9

A

1002-9753(2011)04-0044-10

2010-06-29

2010-11-30

國家自然科學基金創新群體科學基金項目(70921001/G0104,2010-2012),教育部哲學社會科學研究重大課題攻關項目(08JZD0016,2009-2011),國家自然科學基金青年基金項目(71001108)。

陳曉紅(1963-),女,湖南長沙人,中南大學商學院院長,教授、博士生導師,研究方向：不確定性決策、中小企業融資與治理等。