符號動力學在心率變異性分析中的參數選擇*

宋愛玲 黃曉林 司峻峰 寧新寶

(南京大學電子科學與工程學院，生物醫學電子工程研究所，近代聲學教育部重點實驗室，南京 210093)

符號動力學在心率變異性分析中的參數選擇*

宋愛玲 黃曉林司峻峰 寧新寶

(南京大學電子科學與工程學院，生物醫學電子工程研究所，近代聲學教育部重點實驗室，南京 210093)

(2010年4月30日收到;2010年5月24日收到修改稿)

時間序列的符號動力學信息熵 Hk因其計算簡單快速，對數據量要求小，而被應用于心率變異性(heart rate variability，HRV)分析，然而符號化的參數選擇至今卻并未形成統一標準.HRV作為典型的生理信號，存在著極大的個體間差異和非平穩性，要獲得穩健的一致性分析，在符號化過程中必須考慮符號化參數 α與序列本身均值、標準差的綜合影響.文中，首先以仿真噪聲序列為對象，考察了3個參數對于Hk的影響及三者相互之間的關聯性，研究表明當滿足特定關系時，Hk的曲線簇收斂于反映序列動力特性的Hk-up;隨后在對15例心跳間隔序列的分析中，驗證了Hk-up在消除個體間差異及減弱非平穩干擾影響兩方面都優于α取固定值時的研究結果.

符號動力學，熵，心率變異性

PACS:05.45.Tp，87.19.Hh

1.引 言

健康人的逐拍心率或心跳間隔不是整齊劃一的，而是存在著微小的波動［1，2］，俗稱心率變異性(heart rate variability，HRV).HRV的存在絕不僅是外界刺激的結果，而是由心臟作為復雜的多輸入的非線性系統的本質造成，即使是健康人在安靜狀態下也普遍存在［3］.目前所知的健康人的心率至少受3個因素——自動竇性節律、交感神經以及副交感神經的影響［1—3］，而去神經支配后的自動竇性節律是相對穩定的，因此，HRV主要反映了自主神經系統對心臟功能的調控.以往研究表明:自主神經系統與心血管疾病以及心源性猝死有著密切聯系，例如由于交感張力的升高與副交感張力的降低，使室顫閾降低，易引發室速、室顫和猝死，而HRV的降低則可以作為急性心梗后死亡的強有力的獨立的預測因子［4，5］.同時，對于許多其他與自主神經功能相關的非心臟性疾病，如糖尿病、睡眠呼吸停止、癲癇等，以及運動醫學等方面，HRV也具有重要的臨床診斷或研究價值［6—8］.

HRV的分析方法主要包括線性方法和非線性方法兩大類［1，2］.其中如頻域分析等傳統的線性方法至今仍被廣泛應用于臨床診斷.20世紀90年代以后，隨著對心率波動信號的非線性本質的認識的逐步深入［9］，HRV的非線性分析成為研究的熱點［2，10］.盡管HRV的非線性分析目前在臨床應用中還未形成普遍的統一的標準，但是作為心臟動力系統非線性本質的刻畫，非線性方法仍然顯示出其獨特的重要性［11］.

在HRV的非線性分析中，有一類方法——與符號動力學相結合的熵分析方法，由于其對數據長度要求小，計算簡單快速，而顯得極具吸引力.在該類方法中，首先將時間序列，例如心跳間隔序列，在幅度域上進行符號化(粗粒化)編碼，從而將模擬量的時間序列簡化為由有限個符號構成的符號序列，然后考察某一固定長度下時間序列中各種子串模式的出現概率，并對其求信息熵.幅度域的符號化一方面極大地提高了計算速度，另一方面，如果方式選擇得當，盡管會丟失一些細節信息，但卻能在保存動力系統的本質特性的同時大大降低噪聲的影響，因此選擇恰當的符號化依據成為符號化熵分析方法中的關鍵.符號化依據的選擇一般有3種方式: 1)以整個時間序列的均值或方差為基準作為符號劃分的閾值［12，13］，或直接定義臨界點［14］，例如Kurths等［12，13］提出的符號動力學信息熵;2)以時間序列的局域波動作為符號劃分的依據，例如李錦等［15］提出的基本尺度熵;3)以時間序列中相鄰兩點的差值(一階差分)作為符號化的依據，例如卞春華等［13，16］提出的符號序列熵.后兩種方法中，無論是以局域波動作為符號劃分的依據，還是以時間序列的一階差分作為編碼的依據，其結果都忽視了時間序列的整體信息或低頻特性［17］，例如在對高斯白噪聲的基本尺度熵計算中，其熵值遠遠達不到理論值，而不同類別信號間的差異也因為低頻信息的丟失而大大減小，不利于信號的區分.對于這兩種方法的具體討論，可參考文獻［13，15—17］.本文中主要討論的是第一種方法，即符號動力學信息熵的參數影響及其選擇依據.

2.符號動力學信息熵

符號動力學信息熵最早由 Kurths等［12，13］提出，其計算方法如下:對于數據長度為N的時間序列{xi}(1≤i≤N)，將其轉換成符號序列{si}(1≤i≤N)，其中si∈{0，1，2，3}，具體的轉換方法如下:

式中μ代表時間序列{xi}的均值，α則為一個特殊參數.

對于符號序列{si}，其中所有長度為m的子串的集合可表示為{Wj}(1≤j≤N-m+1)，Wj=(sj，sj+1，…，sj+m-1)，考察{Wj}的分布特性，即對出自符號表{0，1，2，3}的長度為m的所有可能的4m個符號串，統計其在{Wj}中出現的次數C(l)(1≤l≤4m)，并估計出概率

對其計算信息熵

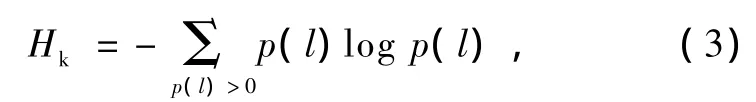
從而得到時間序列{xi}的符號動力學信息熵.Hk反映了時間序列在符號化以后各種長度為m的子串的模式豐富程度和分布特性，出現的符號串模式越多、分布越分散，則熵值越高;符號串模式越少、分布越集中，則熵值越低.例如，對于時間上無相關的完全隨機序列，如高斯白噪聲序列，其長度為m的子串在字符表{0，1，2，3}中取值的可能組合共有4m種，且各種組合模式出現的概率基本一致，因而計算得到的熵值達到最大值log(4)，而對于有特定時序結構的序列，其子串的模式則會遠遠小于4m，同時在分布上也很可能出現不均衡現象，從而熵值小于log(4m).

關于計算Hk時參數的選擇，子串的長度m的增加會導致計算量及必要數據長度的指數增加，而對于結果卻無本質影響，因此，一般取到3就足夠了［12，13］;時間序列長度N的選擇，為使得Hk具有統計學意義，一般要求N4m［12］;而符號化過程中的參數選擇則非常重要.從(1)式可以看出，序列{xi}的均值μ和參數α都會影響符號化的結果，另外，盡管(1)式中沒有直接反映，但是可以推斷，序列{xi}的標準差(standard deviation，SD)也會影響符號化的結果.事實上，這三個參數并非完全獨立，而是相互關聯的.在以往研究中，Kurths和 Wessel等只給出了在研究HRV時，α可以取0.1［12］或者取0.03到0.07之間［13］，然而，HRV作為典型的生理信號，個體間差異大，且同一個體也往往存在著極大的非平穩性，固定的參數選取會導致分析結果受到心跳間隔序列的均值、標準差等參數的影響，而無法獲得穩健的一致性結果.因此，在下面的章節中，將進行詳細的符號化參數分析.

3.基于仿真噪聲序列的符號化參數分析

本節將以仿真噪聲序列為例詳細討論3個參數的影響以及相互之間的關聯性.

3.1.μ，α和SD對Hk的影響

首先以高斯白噪聲序列為對象，考察μ，α和SD對于Hk計算的影響.為簡化起見，事先將長度N= 1000的噪聲序列進行了零均值和歸一化標準差的預處理，然后人為地改變其μ或者SD，并計算不同α取值時的Hk，計算中，取m=3.結果如圖1所示，其中圖1(a)為固定SD=1時，Hk隨μ和α變化的曲線，圖1(b)為固定μ=10時，Hk隨SD和α變化的曲線.

圖1 高斯白噪聲序列Hk隨α，μ，SD的變化情況 (a)固定SD時，隨μ變化的Hk-α曲線簇，(b)固定μ時，隨SD變化的Hk-α曲線簇

從圖1中可見，Hk的值隨著時間序列的 μ，SD以及參數 α的變化而變化，即不同的序列均值、標準差和參數α都會影響計算出來的Hk;另一方面，對于多數α-Hk曲線，都存在著一個極大值，不同曲線的極大值基本相等，即收斂于一個固定值，這里定義為Hk-up，該值非常接近理論推導值 log(43)，這說明:在μ，SD，α三個參數的特定組合下，Hk能達到理論值，從而能夠正確的反映時間序列的內在動力學特性;而參數取值不當時，Hk則可能會遠遠小于log(43)，從而不能真實地反映序列的復雜程度.

除了高斯序列，我們還對1/f噪聲和布朗噪聲做了相同的計算.計算結果顯示，對于這兩種噪聲序列，其Hk隨著μ，SD以及α的變化情況與圖1類似，并且 α-Hk曲線簇也存在著收斂的極大值Hk-up——1/f噪聲為3.5，布朗噪聲為1.9.1/f噪聲和布朗噪聲都存在著時間相關性，兩者的區別在于尺度因子的不同.對于存在時間相關的序列，其長度為m的子串會集中在相對有限的模式，因而其Hk理論上應小于無時間相關性的高斯序列，且尺度因子越大，相關性越強，其 Hk則越小，這與我們的計算結果是相符的.

圖2 獲得Hk-up時的μ-α關系曲線 (a)高斯白噪聲，(b)1/f噪聲，(c)布朗噪聲

3.2.最佳參數設置

既然對于三種典型噪聲序列，其α-Hk曲線簇的極大值都收斂于Hk-up，并且通過高斯序列已經驗證了Hk-up與理論值非常接近，我們推斷Hk-up可以作為時間序列復雜性的一種穩健的反映.下面仍然以上述三種仿真噪聲序列為對象，考察要獲得 Hk-up，μ，SD以及α之間必須滿足的關系.簡單起見，這里將SD固定為1，著重研究μ-α關系.固定μ時，SD-α關系可以類似方法獲得，在此不贅述.

圖2中分別是2000點的標準差為1的高斯序列(a)，1/f噪聲序列(b)，布朗噪聲序列(c)獲得Hk-up時，μ-α關系雙對數曲線.從圖2中可見，三種序列與Hk-up對應的μ-α關系雙對數曲線都呈現出非常明顯的線性，因此，針對三種噪聲各150例獨立的序列，進行了μ-α關系雙對數曲線的線性回歸并作了F檢驗，詳細結果列于表1.

表1 基于仿真噪聲序列的μ-α雙對數曲線線性回歸

從表1中可看出，μ在2.5—100之間時，經 F檢驗證實，三種噪聲μ-α關系的雙對數曲線的線性關系顯著，且線性擬合的斜率均近似為-1，截距也都在-0.4附近.三種噪聲之間，無論是擬合的斜率還是截距，差異均不顯著(t檢驗P>0.05)，這說明:對于這三種存在不同時序結構的序列，要獲得反映其動力學復雜性的 Hk-up，當 SD=1時，其 μ-α關系遵循基本同等的規律，即滿足

由(4)式可以看成在計算符號動力學信息熵Hk時參數選取的最佳方案.有了這個標準，按(1)式符號化時，時間序列單純由均值、標準差的線性變化帶來的影響基本被消除.

4.HRV的分析應用

在本節中我們研究的序列來自于Chaos在2008年發起的專題討論“正常心率是混沌的嗎?”所提供的數據庫*，其中包括 5例正常竇性心率(normal sinus rhythm，NSR)(年齡30±10)，5例充盈性心衰(congestive heart failure，CHF)患者(年齡59±9)，5例房顫(atrial fibrillation，AF)患者(年齡不詳)的長時(20—24 h)心跳間隔序列.生理信號的個體差異和非平穩性，一直是阻礙其分析獲得穩健的一致性結果的一個重要原因.例如在HRV研究中，采集心電數據時不同個體之間所處狀態的差異，以及單個個體在持續心電采集時心跳間隔序列的非平穩性，都會嚴重影響到分析結果.本節中，針對上述兩種情況，分別研究了利用最佳參數設置后，符號動力學信息熵對于HRV分析的改善.

首先對所有15例數據的最初2000點，分別利用固定參數，取 α=0.05(仿照文獻［13］)，α= 0.01，以及第3節得到的最佳參數設置方法，計算了各自的符號動力學信息熵，分別記為 Hk1，Hk2和Hk-up，結果如圖3所示.圖3中，橫軸是15例數據的編號，其中1—5為NSR(n1nn—n5nn)，6—10對應CHF患者(c1nn—c5nn)，11—15則對應 AF患者(a1nn—a5nn);縱軸是符號動力學信息熵 Hk的計算值;圖中‘’代表應用最佳參數方案獲得的熵值Hk-up，而‘*’和‘+’則分別代表不考慮個體間均值差異而固定取α=0.05時的熵值Hk1和 α=0.01時的熵值Hk2.

圖3 心跳間隔序列的Hk1，Hk2和Hk-up結果比較

由圖3可見，三組樣本的 Hk-up相對于Hk2都有明顯的改變，而對于 ID為4以及7—15的序列，Hk-up與 Hk1也有顯著的差別，特別是，采用 Hk-up時，AF患者完全與NSR和CHF區分開來，同時AF類別內的個體差異也明顯減小.為進一步說明利用Hk-up更能反映序列的動力學本質而盡可能排除均值等線性因素的影響，圖4中分別給出了CHF組(a)和AF組(b)的μ—Hk的散點圖，圖中實線代表擬合直線.從圖4中可見，Hk-up與序列均值的線性相關性相對于Hk1，Hk2減小，這說明，采用標準化參數后，組內成員之間盡管采樣時存在均值、標準差等狀態的不同，Hk-up仍然能真實地反映動力系統的復雜性，從而獲得一致性的結果.

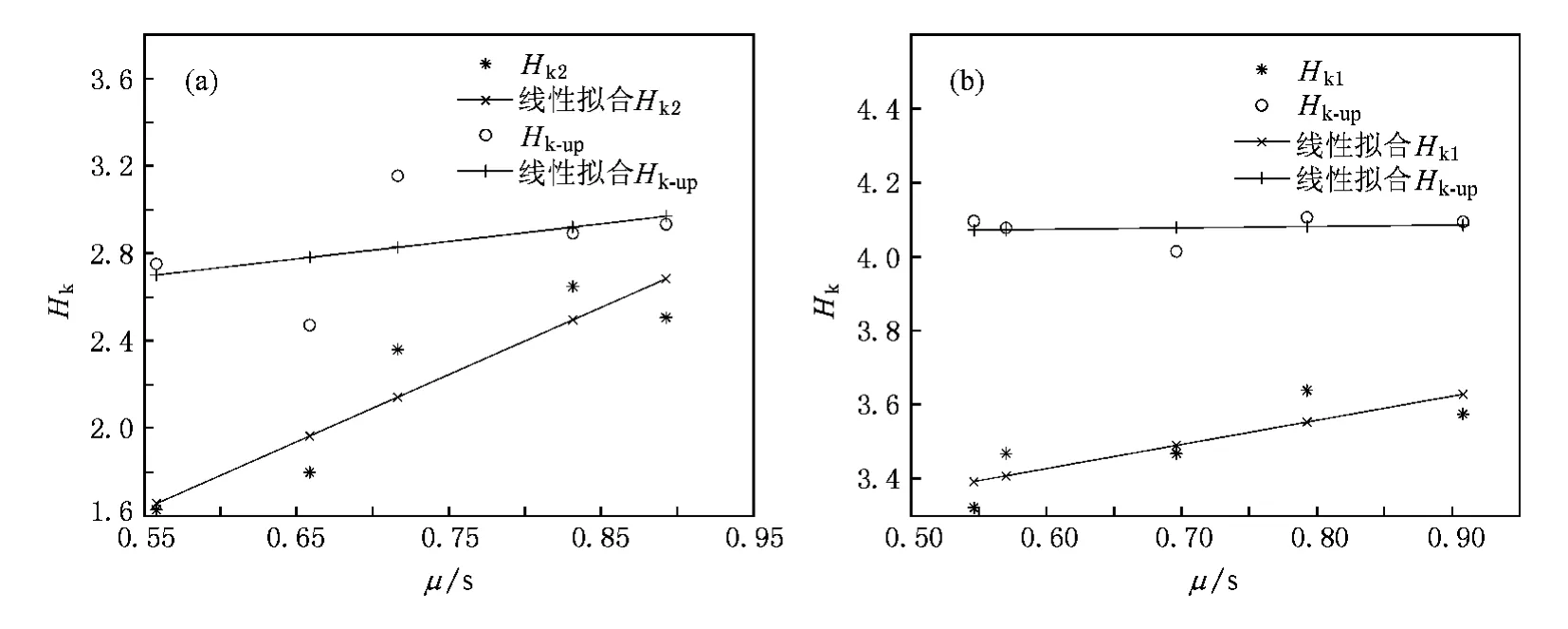
圖4 心跳間隔序列的μ—Hk散點圖 (a)CHF組，(b)AF組

接下來，則通過對長時數據的分段分析來考察在同一個體中，Hk-up減弱均值波動影響的能力.對于每例數據，我們都將其按2000點一段分為31段，分別計算每段的均值、Hk1、Hk-up，再考察每例樣本Hk1，Hk-up的波動范圍及其與均值之間的相關性，對于線性相關顯著(P<0.05)的則對其進行線性擬合，比較線性擬合的斜率，圖5畫出了具有代表性的a1nn數據的分段分析結果，其中圖5(a)為熵值隨分段時間的波動，其橫軸代表分段的序號，縱軸代表符號動力學信息熵，圖5(b)則為其μ—Hk的散點圖，實線代表線性擬合.由圖5可見，就 a1nn而言，Hk-up的波動范圍明顯小于 Hk1，且 Hk-up對于 μ的線性依賴性也顯著降低.三組共15例樣本的全部結果列于表2中，其中，Δ代表參數的值域，k代表線性擬合的斜率，NS代表線性相關不顯著(P>0.05).

從表2中可以看到，就熵值的變化范圍而言，除了n3nn，c1nn，c4nn(表中有下劃線的數據)以外，其他樣本中Hk-up波動都是小于 Hk1的;而從 μ—Hk的相關性分析及線性擬合斜率來看，除了n3nn(表中有下劃線數據)的 Hk-up隨 μ的變化比 Hk1大，n4nn，n5nn，c1nn，c4nn兩種熵值與μ均無顯著線性相關，其他樣本都表現出 Hk-up隨 μ的變化減小或者與 μ的線性相關性的削弱.這兩個方面都說明，采用最佳參數設置后的Hk-up對于HRV的復雜性描述更穩定，更不易受均值波動的影響.而在三組樣本中，以AF組的改善效果為最好，這是由于 α取固定值0.05，即是文獻［13］在完全不考慮 AF病人的前提下針對正常范圍的平均心率和標準差情況挑選過的，所以就NSR，CHF而言該α與最佳參數偏離不是特別大，而AF組其均值和標準差較NSR和CHF組有較大偏離，因而α取0.05的選擇嚴重偏離其最佳參數，從而造成看起來Hk-up對于 AF組的改善效果最好.

圖5 a1nn的長時心跳間隔序列分段分析 (a)Hk隨分段時間的波動情況，(b)μ—Hk散點圖

表2 長時心跳間隔序列分段分析的Hk波動范圍及與μ的線性相關性分析

圖6為三種噪聲和三組HRV的Hk-up值的比較.

由圖6可見，AF組可以完全與NSR和CHF組區分開來，而且與高斯噪聲接近，而NSR和CHF組的Hk-up則處于1/f噪聲和布朗噪聲之間.這說明，AF患者的心跳間隔序列存在著嚴重的時間相關性缺失，其隨機性與白噪聲接近，而NSR和CHF患者的心跳間隔序列則存在著時間相關性，這種相關性比1/f噪聲略強，而比布朗噪聲又要弱，這與以往通過功率譜或去趨勢波動(detrended fluctuation analysis，DFA)等方法得到的研究結果是一致的［18，19］.

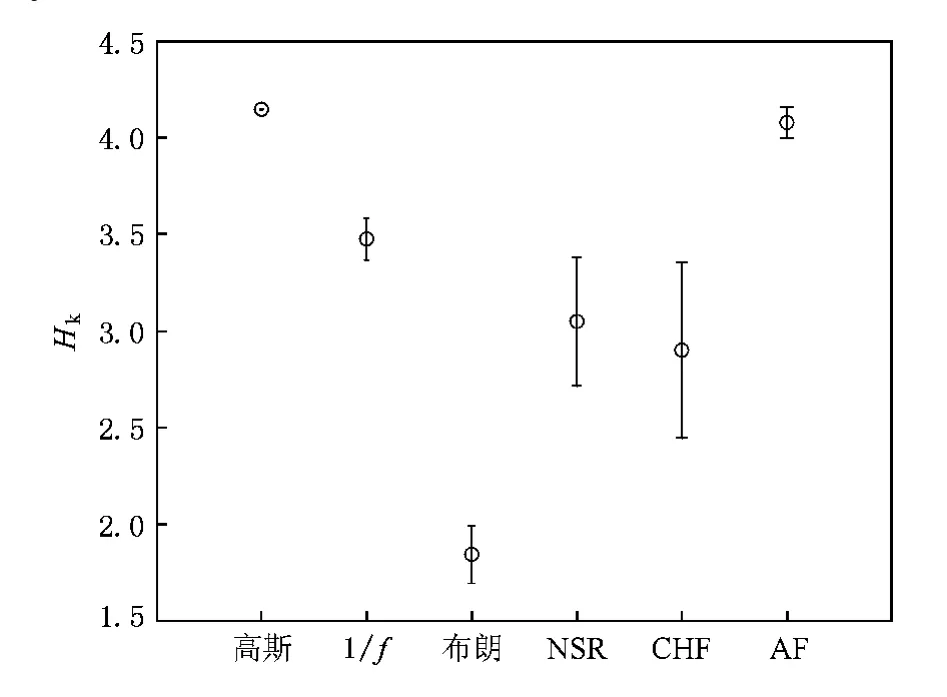
圖6 仿真噪聲和HRV的Hk-up對照

5.討論和結論

以往研究表明，心率波動序列作為確定性系統產生的非隨機序列，僅由概率分布函數來描述是不夠的，其排列的先后順序也蘊含了大量的內在動力學特性［1］，符號動力學信息熵則能從一定程度上衡量這種時間前后的關聯性，從而評價時間序列的復雜性.符號動力學信息熵計算簡單快速，對數據量要求不大，但是符號化參數的選取一直以來并未形成統一標準，而HRV作為生理信號的一種，具有個體間差異大和非平穩等特點，因此，如何盡量消除個體差異使參數具有可比性，以及如何消除非平穩干擾的影響而獲得一個穩健的一致性的分析結果，使得為符號化建立一個參數選取的最佳方案成為必須解決的問題.

本文對符號動力學信息熵Hk的符號化方法進行了參數分析:首先通過三種代表性的仿真噪聲序列(高斯噪聲、1/f噪聲、布朗噪聲)，研究了符號化參數α與序列本身均值、標準差的影響及相互關聯性，結果表明當 α與均值、標準差滿足特定關系((4)式)時，Hk會收斂于反映真實動力學特性的Hk-up;然后，針對三組共15例心跳間隔序列驗證了利用最佳參數設置方案的 Hk-up無論是消除不同個體間狀態差異，還是減弱同一個體在長時心電采集中的基礎心率的影響，都優于固定α的Hk.最后，通過比較三組HRV與三種噪聲的Hk-up，認為AF組心跳間隔序列在時間相關性上與高斯白噪聲基本接近，而NSR組和CHF組則更接近1/f噪聲，即NSR和CHF組的心跳間隔序列存在著類似1/f噪聲的時間相關性，這與以往研究認為正常人 HRV包含1/f成分［18，19］的觀點是相符的.

同時我們也看到，在NSR和CHF組的Hk-up分段分析結果中，Hk-up仍然存在著不可忽略的波動，既然基礎心率等線性非平穩干擾帶來的影響已經消除，那么 Hk-up的波動很可能是由心臟動力系統本身固有的低頻特性所引起，2000點的心跳間隔序列不足以包含這種低頻成分，這很可能就是導致NSR組和 CHF組之間僅由 Hk-up無法區分的重要原因.要詳細研究這些低頻成分，需要有大量的長時心跳間隔序列，并且要在采集過程中嚴格標定測試者各個時間段的狀態，這將是我們進一步工作的方向.

感謝南京郵電大學地理和生物信息學院馬千里博士對文中噪聲的獲得和處理提出的寶貴建議.

［1］Camm A J，Malik M，Bigger J T，Breithardt G，Cerutti S，Cohen R J，Coumel P，Fallen E L，Kennedy H L，Kleiger R E，Lombardi F，Malliani A，Moss A J，Rottman J N，Schmidt G，Schwartz P J，Singer D H 1996 Eur.Heart J.17 354

［2］Kleiger R E，Stein P K，Bigger J T 2005 A.N.E.10 88

［3］Ivanov P C，Chen Z，Hu K，Stanley H E 2004 Physica A 344 685

［4］Kleiger R E，Miller J P，Bigger J T，Moss A J 1987 Am.J. Cardiol.59 256

［5］Malik M，Farell T，Camm A J 1990 Am.J.Cardiol.66 1049

［6］Huikuri H V，Makikallio T H，Airaksinen K E J，Seppanen T，Puukka P，Raiha I J，Sourander L B 1998 Circulation 97 2031

［7］Stein P K，Kleiger R E 1999 Annu.Rev.Med.50 249

［8］Zhuang J J，Ning X B，Zou M，Sun B，Yang X 2008 Acta Phys. Sin.57 2805(in Chinese)［莊建軍、寧新寶、鄒 鳴、孫 飆、楊 希2008物理學報57 2805］

［9］Li C，Tang D K，Fang Y，Sun J T，Ding G H，Poon C S，Wu G Q 2009 Acta Phys.Sin.58 1348(in Chinese)［李 程、湯大侃、方 勇、孫錦濤、丁光宏、Poon C S、吳國強2009物理學報58 1348］

［10］Ning X B，Bian C H，Wang J，Chen Y 2006 Chin.Sci.Bull. 51 385

［11］Wessel N，Riedl M，Kurths J 2009 Chaos 19 028508

［12］Kurths J，Voss A，Saparin P，Witt A，Kleiner H J，Wessel N 1995 Chaos 5 88

［13］Wessel N，Ziehmann C，Kurths J，Meyerfeldt U，Schirdewan A，Voss A 2000 Phys.Rev.E 61 733

［14］Liu X F，Yu W L 2008 Acta Phys.Sin.57 2587(in Chinese)［劉小峰、俞文莉2008物理學報57 2587］

［15］Li J，Ning X B，Wu W，Ma X F 2005 Chin.Phys.14 2428

［16］Bian C H，Ma Q L，Si J F，Wu X H，Shao J，Ning X B，Wang D J 2009 Chin.Sci.Bull.54 4610

［17］Huang X L，Cui S Z，Ning X B，Bian C H 2009 Acta Phys. Sin.58 8160(in Chinese)［黃曉林、崔勝忠、寧新寶、卞春華2009物理學報58 8160］

［18］Kobayashi M，Musha T 1982 IEEE Trans.Biomed.Eng.29 456

［19］Peng C K，Havlin S，Stanley H E，Goldberger A L 1995 Chaos 5 82

PACS:05.45.Tp，87.19.Hh

Optimum parameters setting in symbolic dynamics of heart rate variability analysis*

Song Ai-Ling Huang Xiao-LinSi Jun-Feng Ning Xin-Bao
(Key Laboratory of Modern Acoustics of Ministry of Education，Institute of Biomedical Electronic Engineering，School of Electronic Science and Engineering，Nanjing University，Nanjing 210093，China)

30 April 2010;revised manuscript

24 May 2010)

The Shannon entropy Hkin symbolic dynamics analysis of time series has less data demand and can be complemented easily，and therefore is applied to heart rate variability(HRV)analysis.However，the criterion has not been established as to the parameter α，which is used during the transformation into symbols.Like all other physiological signals，great differences between individuals as well as nonstationarity are usual in HRV.Therefore，to achieve a robust and consistent analysis，the parameter α should be considered together with the mean and standard error of the series.In this paper，the integrative effects on Hkof the three parameters were studied firstly in simulation time series，and it was suggested that under certain conditions，the clusters of Hkapproach a convergent upper boundary named Hk-up，which reflects the intrinsic dynamics of the time series.Then，in the heart beat interval series analysis of 15 subjects，the abilities of Hk-upto alleviate the impacts brought by both difference between individuals and nonstationarity were testified.

symbolic dynamics，entropy，heart rate variability

*國家自然科學基金(批準號:60701002)資助的課題.

*http://www.physionet.org/challenge/chaos/

*Project supported by the National Natural Science Foundation of China(Grant No.60701002).