基于強度統計算法的混沌序列復雜度分析*
孫克輝 賀少波 盛利元
(中南大學物理科學與技術學院,長沙 410083)
基于強度統計算法的混沌序列復雜度分析*
孫克輝賀少波 盛利元
(中南大學物理科學與技術學院,長沙 410083)
(2010年4月8日收到;2010年5月28日收到修改稿)
為了分析混沌序列的復雜度,文中采用強度統計復雜度算法分別對離散混沌系統(TD-ERCS)和連續混沌系統(簡化Lorenz系統)進行復雜度分析,計算了混沌序列隨參數變化的復雜度,分析了連續混沌系統產生的偽隨機序列分別進行m序列和混沌偽隨機序列擾動后的復雜度.研究表明,強度統計復雜度算法是一種有效的復雜度分析方法,離散混沌序列復雜度大于連續混沌序列復雜度,但對連續混沌系統的偽隨機序列進行m序列和混沌偽隨機序列擾動后可大大增加復雜度,為混沌序列在信息加密中的應用提供了理論依據.
強度統計復雜度算法,TD-ERCS系統,簡化Lorenz系統,序列擾動
PACS:05.45.-a,05.45.Tp
1.引 言
混沌序列復雜度是指其接近隨機性的程度,越接近隨機序列,復雜度越大.隨著混沌科學的發展,混沌系統中的復雜性引起了越來越多人的關注,實用的混沌偽隨機碼應具有盡可能大的序列復雜度,以保證擴頻通信的最大通信容量.目前計算序列復雜度的算法主要有四種,都是建立在Kolmogorov復雜度[1]基礎上,前三者分別是1976年由Lempel和Ziv提出的 Limpel-Ziv算法[2]、1991年由 Steven和Pincus提出的復雜性近似熵(ApEn)算法[3]和2002年由 Bandt和 Pompe提出的復雜性度量排列熵(PE)算法[4].這三種算法都能在一定程度上正確反映出混沌序列的復雜度,但 Limpel-Ziv算法只是在一維時間尺度上對系統的復雜度進行統計,涉及的只有序列的長度,而ApEn算法體現了不同嵌入維變化時情況,但是計算過程中涉及嵌入維和分辨率參數的選擇,其結果隨主觀因素而有所變化,對于PE計算結果也要進行嵌入維的選擇[5].第四種是強度統計復雜度算法,強度統計算法最早由 López-Ruiz,Mancini和Calbet(LMC)提出[6],原理是用統計復雜度測度(SCM)作為時間序列內模型結構程度的量化器.對給定的系統狀態,統計復雜度測度是測度熵(H)乘以到平衡狀態(Q)距離的積,對完全隨機過程其值是零.對比前面三種算法,強度統計算法可以看成是對PE算法的進一步改進,因為其考慮了到平衡狀態(Q)距離這一因素,反映了序列內模型結構.文獻[7]進一步改進了強度統計復雜度算法,使之具有強度特性.強度統計復雜度測度更方便應用于序列隨機性的度量,同時能呈現序列的相關結構,反應序列的隨機本質.
本文在討論了強度統計復雜度算法原理的基礎上,以TD-ERCS系統和簡化Lorenz系統為例,分別分析了離散混沌系統和連續混沌系統產生的混沌序列的復雜度,討論了混沌序列復雜度隨系統參數、分數階數而變化的規律,計算了連續混沌系統偽隨機序列在m序列和混沌序列擾動下的復雜度,為混沌序列在保密通信和信息安全方面的應用提供了理論依據.
2.復雜度算法原理與描述
強度統計復雜度測度CJ[P]是一個和動態系統產生的時間序列的概率分布P相聯系的物理量,其計算公式為[8]

其中
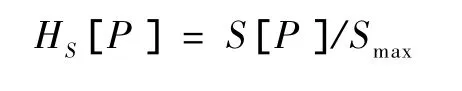
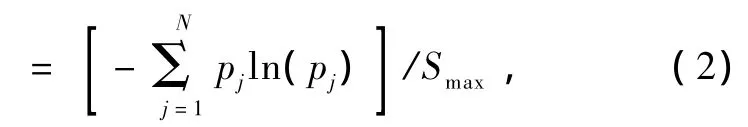
且有Smax=S[Pe]=lnN(0≤HS≤1),N代表系統在相空間中總的狀態數目;Pe表示均勻分布,即Pe= {1/N,…,1/N},S為Shannon熵.QJ是根據 Jensen-Shannon分歧定義的不均衡,有[8]

Q0是歸一化常數,其計算式為
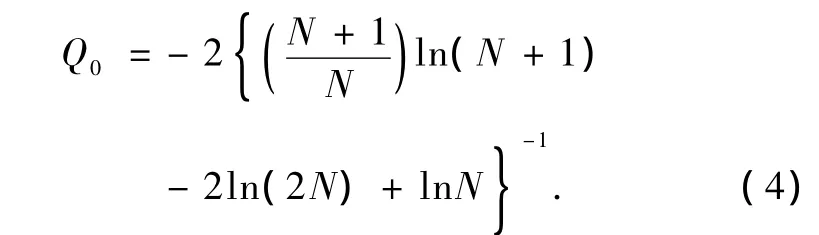
可見,0≤QJ≤1,且不均衡QJ為能反映序列結構的強度量,同樣CJ[P]也能呈現序列的相關結構,對沒有任何結構的完全隨機序列,CJ[P]=0.復雜度測度值越小,則系統復雜度越大,反之亦然.
概率分布P采用Bandt-Pompe提出的方法進行計算[4].給定時間序列{xt,t=1,…,T}和一個嵌入維d>1,對每一時刻i(i=1,2,…,T-d+1),其d階順次模式是由時刻(i,i+1,…,i+d-1)的值組成的d維向量
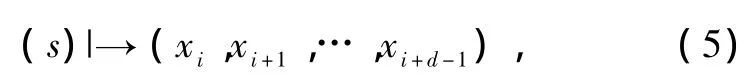
顯然,d越大,向量提供的信息越多.通過和時刻 i聯系的“順次模式”,定義(0,1,…,d-1)的一個排列π=(r0,r1,…,rd-1)為

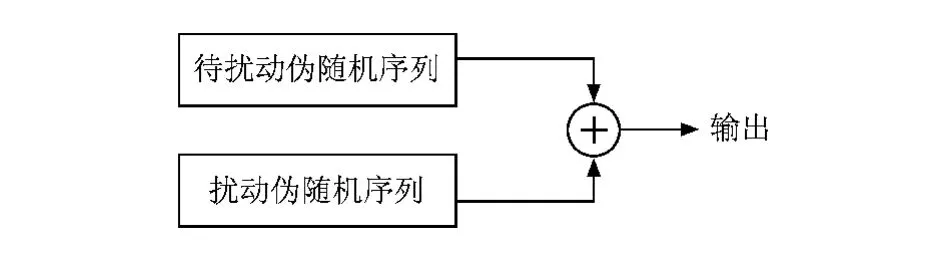
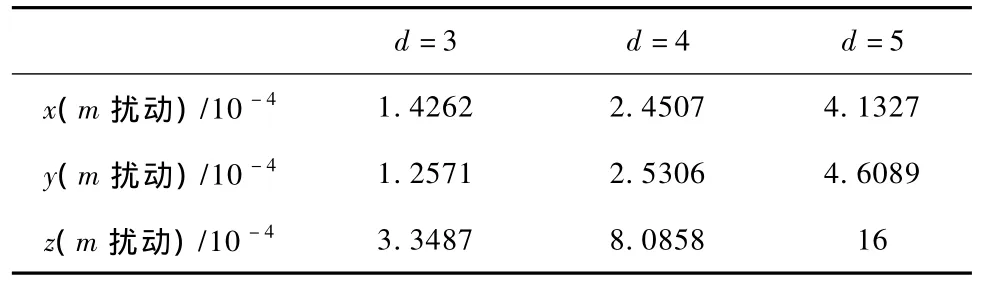
若 xi+ri=xi+ri-1,則 ri 符號#代表“數目”.強度統計復雜度通過這種“排列”概率分布來計算. 值得指出的是,按此種排序方法得來的概率對于周期序列,特別是短周期序列會產生錯誤,如序列{1,2,3,4,1,2,3,4,1,2,3,4,…},當d=3時,P ={1/2,1/4,1/4},當d=4時,P={1},當d=5時,P={1/4,1/4,1/4,1/4},代入(1)式,當d=3時,復雜度CJ[P]=0.0427,當d=4時復雜度不存在,當d=5時復雜度CJ[P]=0,但顯然序列不是完全隨機的. 下面以基于切延遲的橢圓反射腔離散混沌系統(TD-ERCS系統)[9],Logistic系統和耦合映像格子系統[10]為例,證明強度統計復雜度算法的有效性和分析離散系統的復雜度特性. TD-ERCS系統映射關系為 其中 其中,參數(u,x0,α,m)為系統的種子參數,確定了系統種子參數,系統特性也就隨之確定,且有u(0< u≤1),x0(-1≤x0≤1),α(0<α<π),m=0,1,2,3,….當m=0時系統為ERCS系統,當m=1,2,3,….時系統為 TD-ERCS系統,并處于混沌狀態.對(8)式進行迭代就能分別得到兩個實值序列{xm+1,xm+2,xm+3,xm+4,…}和{km+1,km+2,km+3,km+4,…}. 取系統初值x0=0.7654,α=0.9876,系統參數u=0.7123,迭代次數N=10000,嵌入維d分別為3,4,5.對系統的不同切延遲 m情況進行強度統計復雜度計算,結果如表1所示. 表1 TD-ERCS系統的強度統計復雜度 由表1可見隨著嵌入維d的增加,即子序列反映的信息增加,總的趨勢是復雜度有所增大,但相差不大.當m=0時,系統復雜度最小,比m=1時小一個數量級;當m=2時,系統的復雜度又增大了一個數量級;m=3時與m=2時的系統復雜度基本一樣.這說明強度統計復雜度算法是一種很有效的方法,能很好地識別出系統復雜度. 為了進一步分析系統復雜度,這里考察系統參數u,m變化時復雜度的變化情況.系統復雜度隨參數變化的情況如圖1所示,嵌入維為d=3. 圖1 TD-ERCS系統復雜度隨系統參數變化情況 (a)m=2,u變化,(b)u=0.7123,m變化 如圖1(a)所示,隨著u值的增加系統復雜度增加,最后趨于穩定,從u的物理意義來看,u越接近1則橢圓反射腔越接近圓,其反射效果也越接近圓的反射效果,系統復雜度也就越大;從圖1(b)可以看出,當m=0時,系統復雜度最小,此時系統為ERCS系統,但隨著m的增加,系統復雜性增大并處于基本穩定狀態,保持在0—0.005之間,可見當 m≥2后,切延遲操作對系統復雜度影響不是很大.綜上可知TD-ERCS系統是一個廣域高復雜性混沌系統. Logistic系統和耦合映像格子系統迭代方程參見文獻[10],系統相圖也參見該文獻中的圖2(a)和(b).可見耦合映像格子系統相圖比Logistic系統相圖“混亂”,其復雜度應該比Logistic系統大很多.這里用強度統計算法計算這兩者的復雜度如表2所示. 表2 Logistic和耦合映像格子復雜度 計算結果與實際情況符合,耦合映像格子序列復雜度比Logistic大2個數量級,可見,強度統計復雜度算法靈敏性很好.文獻[10]中的表2,兩系統產生的8進制偽隨機序列的復雜度,計算方法采用的是ApEn算法,Logistic的為0.692左右,而耦合映像格子的為2.00左右,相比強度統計算法的計算結果區分度小很多,雖然計算的不是同一種序列. 下面取以上三個系統在不同迭代次數N情況下,計算序列強度統計復雜度與長度 N的關系.這里嵌入維d=5,各系統參數的選擇與上面的基本一致,其中TD-ERCS系統的切延遲(m=3),計算結果如表3所示. 表3 復雜度隨序列長度的變化情況 由表3可知,系統產生的序列的長度對復雜度的影響不大.這點明顯優于 Limpel-Ziv算法,因Limpel-Ziv算法涉及長度N的選擇,復雜度隨 N的增大有減小的趨勢[5].另外,對比表1,2,3可知,耦合映像格子系統復雜度比TD-ERCS系統的高,因為耦合映像格子系統為6維系統,而TD-ERCS系統是2維的,TD-ERCS系統復雜度小一點,但其運算量相對較小. 對離散系統的復雜度分析可以看出強度統計算法是一種非常有效的復雜度分析方法,從前面的計算結果來看,當只改變嵌入維d或序列長度N時,序列的復雜度改變不是很大,且復雜度對比結果不改變,也就是說在比較序列復雜度時只要選取一樣的嵌入維d和序列長度N,按照強度統計算法計算復雜度值,就可以了,在這里,考慮到計算量問題,我們給出兩者的參考值,嵌入維d取3即可,或4和5也可以,但再大就沒必要了,因為當d≥6時,d!就比較大了,這樣概率分布P的獲取將非常繁雜,而序列長度N的選擇根據具體情況而定,一般1000≤N≤10000都可以滿足條件,再大也沒太多意義;另外就是離散系統的復雜度是比較高的,復雜度值最大可以達到10-4數量級. 圖2 簡化Lorenz系統吸引子相圖 (a)分數階,(b)整數階 Lorenz系統族是著名的混沌系統,在文獻[11]中將其歸為一類,并以統一的形式表達,而簡化Lorenz系統[12]為 Lorenz系統族的一員.這里,選取簡化Lorenz系統為例,研究連續混沌系統的復雜性特點. 簡化Lorenz系統方程為 其中c為系統參數,α,β,γ為微分階數,當α=β=γ =1時,系統為整數階簡化Lorenz系統;當0<α,β,γ<1時,系統為分數階簡化 Lorenz系統.圖2為簡化Lorenz系統的吸引子圖,參數選擇為分數階α=β =γ=q=0.98,c=5,整數階α=β=γ=q=1,c=5,可見此時系統都處于混沌狀態. 當系統處于混沌態時,分別選取系統產生的三個序列,利用強度統計復雜度算法計算在不同嵌入維下的復雜度,其結果如表4所示. 表4 不同嵌入維下簡化Lorenz系統強度統計復雜度 從表4可以看出不管系統是處于整數階狀態還是分數階狀態,其產生的序列復雜度都不是很大,且差別很小.對于同一系統中各序列的復雜度相差也不大.從圖2吸引子圖可以看出 x,y,z三個序列值并沒有分布于整個坐標平面,而在有限空間相互成一定的規律,不是很“混亂”,所以復雜度不會很大.進一步,從計算結果表 4,圖 2可以得出簡化Lorenz系統(q=0.98,1時)復雜度并不是很大.為了證明這一點,接下來考察系統參數對復雜性影響,如圖3所示. 圖3中系統選取為分數階簡化Lorenz系統.圖3(a)中,當參數c由小到大變化時,對x,y,z序列復雜度影響不大,其值在0.262到0.274之間變化,復雜度比較小.圖3(b)中,α=β=γ=q,c=5,可以看出系統復雜度在q比較小(比如q≤0.5)時比較大,但這只是一種“假象”,根據文獻[12]可知,此時系統處于非混沌態,之后當q接近1時系統處于混沌態,但復雜度變小了.由上面分析可知,簡化Lorenz混沌系統的復雜度不如離散混沌系統. 圖3 分數階簡化Lorenz系統強度統計復雜度隨參數c和q變化情況 (a)q=0.98,c變化,(b)c=5,q變化 連續混沌系統由于約束比較多,其產生的混沌序列復雜度并不一定會很高,如簡化Lorenz系統(q =0.98,1時).在應用中,連續系統由于其參數較多,系統關系復雜,經常被采用,但是往往也需要復雜性高的序列,另外就是實際應用中用得很多的是偽隨機序列.針對這種情況,下面將分別采用m序列和混沌偽隨機序列擾動的方法增加序列的偽隨機序列復雜度.這種方法同樣適用于離散混沌系統. 混沌偽隨機序列是由混沌迭代產生的序列{xn},歸一化后,經過量化和判決得到的,判決公式為[13] 可得到二進制的偽隨機序列{Xn}.對于偽隨機序列復雜度的分析的算法由文獻[13]可知,最常用的是Berlekamp-Massey線性復雜度算法,但文章指出該算法并不能有效地區分出序列的復雜度.這里采用強度統計復雜度算法對偽隨機序列進行測度,只是在計算過程中,p(π)的π獲取方法參照文獻[14]. 將分數階簡化 Lorenz系統產生的偽隨機序列按強度統計算法進行計算,得到的結果如表5所示. 計算結果可看出生成的偽隨機序列復雜度大小與原始序列的差不多,也不是很大.在實際應用中是序列的復雜度越大越好,所以,下面分別用 m序列[15]和混沌偽隨機序列擾動的方法提高序列的復雜度.擾動模型見圖4,擾動序列與待擾動序列對應位進行異或運算,得到結果后輸出. 表5 分數階Lorenz系統二進制偽隨機序列的復雜度 圖4 序列擾動原理示意圖 m序列又叫偽隨機序列、偽噪聲(PN)碼或偽隨碼,是一種常用的擴頻序列,在擴頻通信中有著廣泛的應用.m序列的生成可用移位寄存器序列發生器的本原多項式決定.本文將分別采用4階和10階本原多項式來產生m序列. 根據m序列定義,產生m序列進行擾動實驗.表6和表7是將上面的分數階簡化Lorenz系統的偽隨機序列進行m序列擾動,進而得到的復雜度結果,從中可以看出這種方法的特性. 可以看出序列復雜度明顯變大了,分別至少提高了1和2個數量級.可見這種方法對于提高偽隨機序列復雜度是很有效的.進一步分析表6和表7可以看出隨著d的增加強度統計復雜度值增加,說明序列復雜度在減少,且成倍數變化.原因可能是生成的m序列是一個周期序列,這里周期分別是24-1和210-1,隨著 d增大,m序列的周期性影響越突出.可見m序列擾動能夠大大提高序列的復雜度,是一種很實用的方法;缺點就是m序列是一種周期性序列,其周期性可能會對原序列造成影響. 表6 m序列(4階)擾動后分數階Lorenz系統二進制偽隨機序列復雜度 表7 m序列(10階)擾動后分數階Lorenz系統二進制偽隨機序列復雜度 表8 TD-ERCS偽隨機序列擾動后的分數階Lorenz系統偽隨機序列復雜度 接下來利用混沌偽隨機序列對簡化 Lorenz偽隨機序列進行擾動,混沌偽隨機序列采用的是TDERCS系統產生的偽隨機序列,其種子參數(u,x0,α,m)為(0.7123,0.7654,0.9876,3),擾動后偽隨機序列的復雜度如表8所示. 對比表5和表8可見,利用TD-ERCS系統產生的混沌偽隨機序列對 Lorenz系統偽隨機序列進行擾動后序列的復雜度至少提高了一個數量級,且沒有m序列擾動后的明顯周期性影響.表8最后一行是相應TD-ERCS系統的偽隨機序列復雜度,擾動后的序列復雜度也比其大. 利用m序列擾動可以得到更高復雜度的混沌偽隨機序列,但有周期性影響;而混沌偽隨機序列擾動后,沒有周期性的影響,但得到的序列復雜度沒有利用m序列擾動后的高.總的來說兩種方法各有所長,得到的高復雜度混沌偽隨機均可應用于保密通信. 本文利用強度統計復雜度算法分別對離散混沌系統和連續混沌系統的復雜度進行了分析.對離散系統的分析表明強度統計復雜度算法是一種有效的復雜度測度算法,且具有靈敏度高和對參數嵌入維d和序列長度N的選擇要求不嚴格等特點;在對TD-ERCS等系統分析后,可知該離散系統復雜度大;對連續混沌系統的復雜度分析表明,連續混沌系統復雜度沒有離散混沌系統的大,但經m序列和混沌偽隨機序列擾動后,序列復雜度能有效地增大.m序列擾動后,復雜度隨嵌入維 d的增大而變小,原因可能是m序列本身存在周期性,而混沌偽隨機序列擾動無此現象,但復雜度提高程度相對較小,顯然這兩種方法都可以提高混沌偽隨機序列的復雜度,為混沌序列應用于信息加密提供了理論依據. [1]Li M,Vitanyi P M B 1990 Amsterdam:Elsevier Science A 187 [2]Lempel A,Ziv J 1976 IEEE Trans IT-22 75 [3]Steven M,Pincus S 1991 Mathematics 88 2297 [4]Bandt C,Pompe B 2002 Phys.Rev.Lett.88 174102 [5]Sun K H,Tan G Q,Sheng L Y 2008 Acta Phys.Sin.57 3359 (in Chinese)[孫克輝、談國強、盛利元 2008物理學報 57 3359] [6]López-Ruiz R,Mancini H L,Calbet X 1995 Phys.Lett.A 209 321 [7]Larrondo H A,González C M,Martin M T,Plastino A,Rosso O A 2005 Physica A 356 133 [8]González C M,Larrondo H A,Rosso O A 2005 Physica A 354 281 [9]Sheng L Y,Sun K H,Li C B 2004 Acta Phys.Sin.53 2871(in Chinese)[盛利元、孫克輝、李傳兵2004物理學報53 2871] [10]Xiao F H,Yan G R,Han Y H 2004 Acta Phys.Sin.53 2877 (in Chinese)[肖方紅、閻桂榮、韓宇航 2004物理學報 53 2877] [11]Lü J H,Chen G R,Zhang S C,ˇCelikovsky'S 2002 Int.J. Bifurc.Chaos 12 2917 [12]Sun K H,Sprott J C 2009 J.Bifurcation and Chaos 19 1357 [13]Wang L,Wang F P,Wang Z J 2006 Acta Phys.Sin.55 3964(in Chinese)[王 蕾、汪芙平、王贊基 2006物理學報 55 3964] [14]Luo S J,Qiu S S,Chen X 2010 Journal of South China University of Technology 38 18(in Chinese)[羅松江、丘水生、陳 旭2010華南理工大學報38 18] [15]Fan X Q 2009 Computer Engineering& Science 31 20(in Chinese)[范雪琴2009計算機工程與科學31 20] PACS:05.45.-a,05.45.Tp Complexity analysis of chaotic sequence based on the intensive statistical complexity algorithm* Sun Ke-HuiHe Shao-Bo Sheng Li-Yuan 8 April 2010;revised manuscript 28 May 2010) To analyze the complexity of the chaotic sequences,based on the intensive statistical complexity algorithm,the complexities of the discrete TD-ERCS and continuous simplified Lorenz chaotic systems were investigated respectively,and the complexities of the chaotic sequences with different system parameters were calculated.The complexities of pseudorandom sequences of the continuous chaotic systems disordered by m-series and chaotic pseudo-random sequences were analyzed.The results indicate that the intensive statistical complexity algorithm is an effective method for analyzing the complexity of the chaotic sequences,and the complexity of the discrete chaotic systems is larger than that of the continuous ones.However,after disordering by m-series or chaotic pseudo-random sequences,the complexities of the pseudo-random sequences can be increased significantly.This study provides a theoretical basis for the applications of chaotic sequences in the field of secure communication and information encryption. intensive statistical complexity algorithm,TD-ERCS,simplified Lorenz system,sequence disorder *國家自然科學基金(批準號:60672041)資助的課題. *Project supported by the National Natural Science Foundation of China(Grant No.60672041).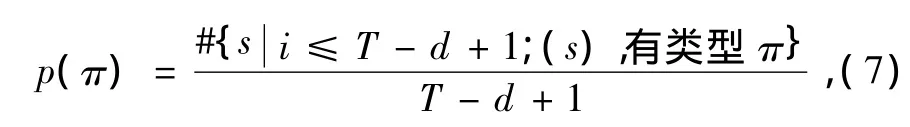
3.離散混沌系統的復雜度分析

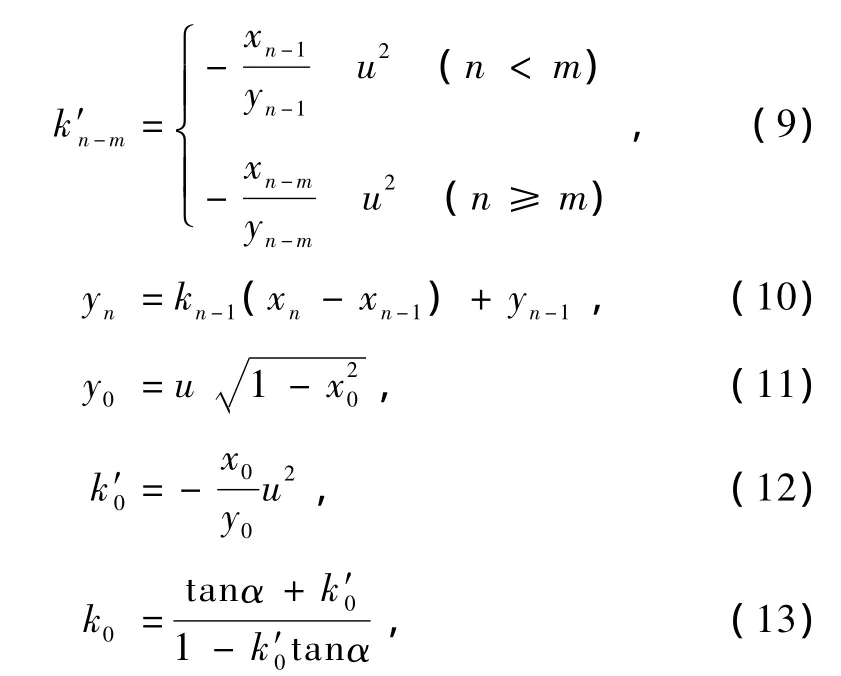




4.連續混沌系統的復雜度分析
4.1.簡化Lorenz系統模型

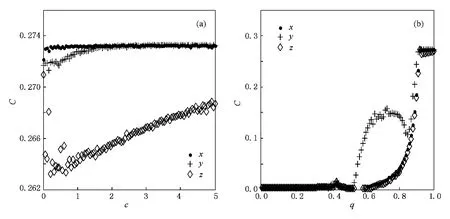
4.2.簡化Lorenz系統復雜度分析

4.3.偽隨機序列生成及序列擾動后復雜度
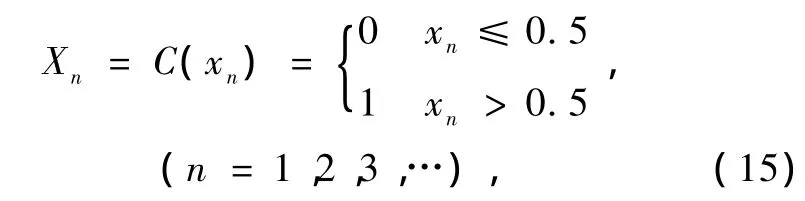



5.結 論
(School of Physics Science and Technology,Central South University,Changsha 410083,China)

