狹長區域GPS水準點的最佳布設與擬合方法的應用探討＊

郭 敏，強曉煥，王宇飛

（1.河南理工大學 測繪與國土信息工程學院，河南 焦作454003；2.中原油田建設集團公司，河南 濮陽457000）

0 引 言

近年來，GPS技術在公路、鐵路、隧道等領域發揮了積極的作用，用該技術建立狹長工程區域的控制網比常規方法省時、省力，而且精度高、速度快。借助于分布在測區的部分GPS點與水準點重合，建立區域的高程擬合模型，這在一些工程中獲得很大的應用，特別是分布較小區域。對于狹長工程區域的控制網，由于其形狀特殊、范圍大，重合點的分布受到限制等，狹長工程區域GPS高程的擬合仍處于研究階段。從點位的最佳布設，結合多面函數擬合法、分區擬合法進行高程轉換，通過精度評定，得出各種方法的適應范圍和精度級別，最終得出狹長區域的最佳布設方案及最佳擬合方法。

1 點的布設

GPS水準點的布設對提高高程精度是非常關鍵的。下面是一個具體實例：狹長的工程區域高程控制必須覆蓋測區，并確保寬度至少達到1km。水平控制必須覆蓋測區。當控制點的間隔僅100 m時，其高程的誤差達到了20mm（見圖1），要提高這種工程的校正控制，需增加水平控制點和高程控制點，保證覆蓋整個測區，并保證高程控制點之間的寬度不小于1km（見圖2）。

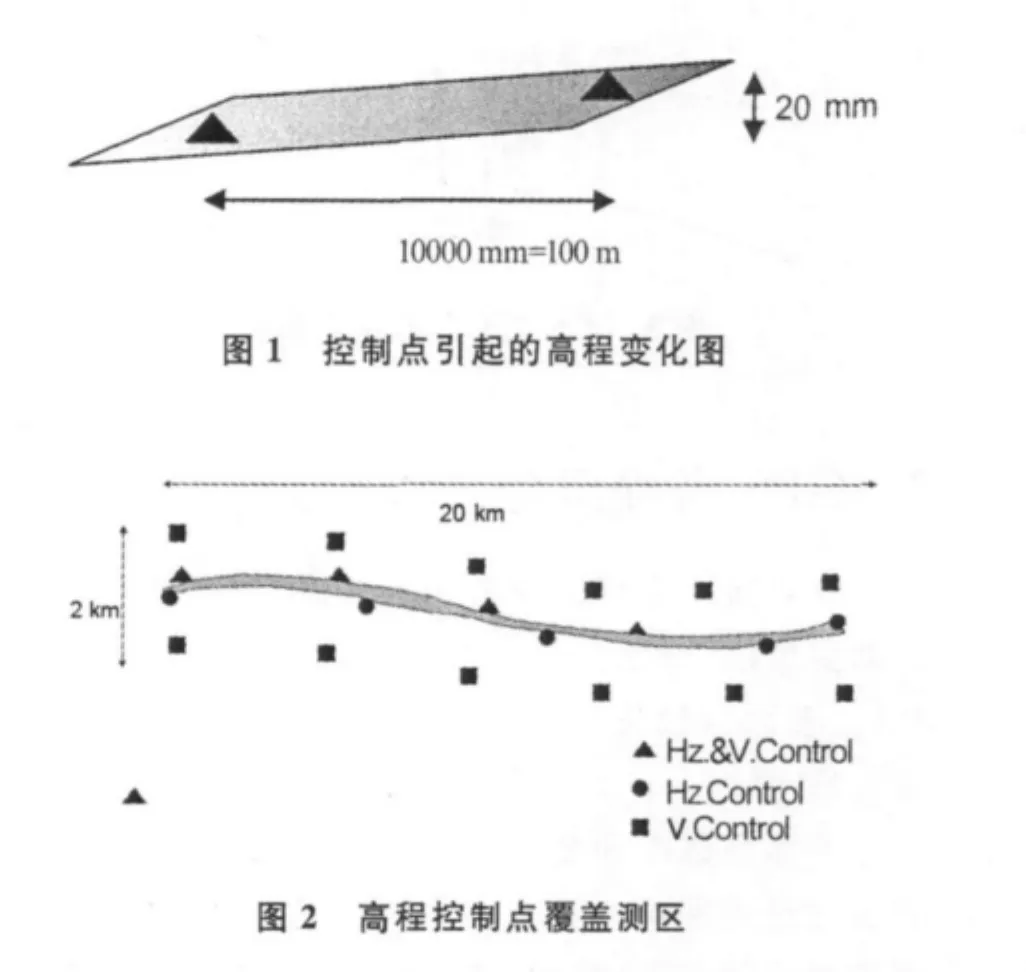
重合點的布設是否恰當，直接關系到擬合精度。從理論上講，這些點最好分布在高程異常的特征點上，即這些點能有效地代表測區的高程異常變化，從而使采用這些點建立起來的擬合曲面能較好地接近實際曲面，否則將會帶來較大的模型誤差。但在實際工作中，由于高程異常的分布與地形的走勢并非一致，選取重合點存在一定的盲目性。實踐證明，重合點的選取應注意以下幾點：①一般根據測區已知水準點的分布并考慮均勻分布的原則確定重合點；②在地形有較大變化的交界處布設重合點；③當擬合區域范圍較大時，可借助該區域全球高程異常圖布設。

2 GPS高程轉換方法

高程轉換方法利用GPS水準高程法，該方法是從幾何解析的角度出發，利用GPS測量和水準測量成果確定似大地水準面，求出高程異常，從而擬合出正常高的一種方法。此方法在工程上已獲得廣泛的應用。見圖3所示各種高的關系，H代表大地高，Hr為正常高，ξ為高程異常，它們之間的關系見公式（1）：

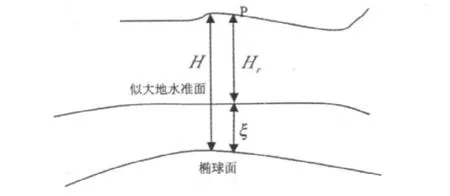
圖3 大地高和正常高關系圖

3 GPS高程擬合方法

針對狹長工程區域常用方法進行探討，重點對多面函數法、分區擬合法兩種方法進行探討。

3.1 多面函數法[1－4]

1）原理

多面函數擬合是一種純數學曲面逼近方法，它的出發點是在每個數據點上同各個已知數據點分別建立函數關系（這種關系表現為一規則的數學曲面），將這些有規律的數學曲面按一定的比例迭加起來，就可擬合出任何不規則的曲面，且能達到較好的擬合效果。也就是一個數學表面上某點（X，Y）處的高程Z的表達式為

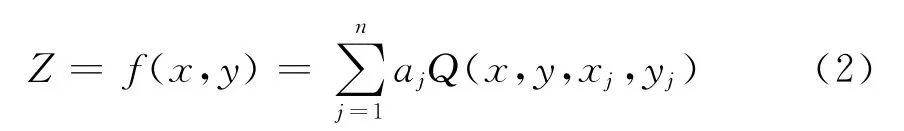
式中：aj是待定系數；Q（x，y，xj，yj）為核函數；x、y為待求點的坐標；（xj，yj）為已知點坐標。選擇式中δ為光滑系數。

當待求點數等于已知點時，任一點ξp為

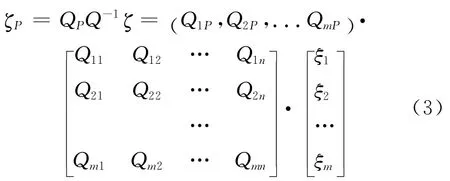
式中，Qij＝Q（x，y，xj，yj）。

當待求點多于已知點數時，

在GPS網中，GPS水準可求出高程異常，取全部或部分已知點為核函數的中心點 （xj，yj）就可用上述方法求出點（xj，yj）上的高程異常，從而獲得該測區的高程異常分布圖。

2）多面函數法精度計算

某狹長區域工程控制網平面示意圖如圖4，表1為控制區的高程成果圖

圖4 示意點位圖

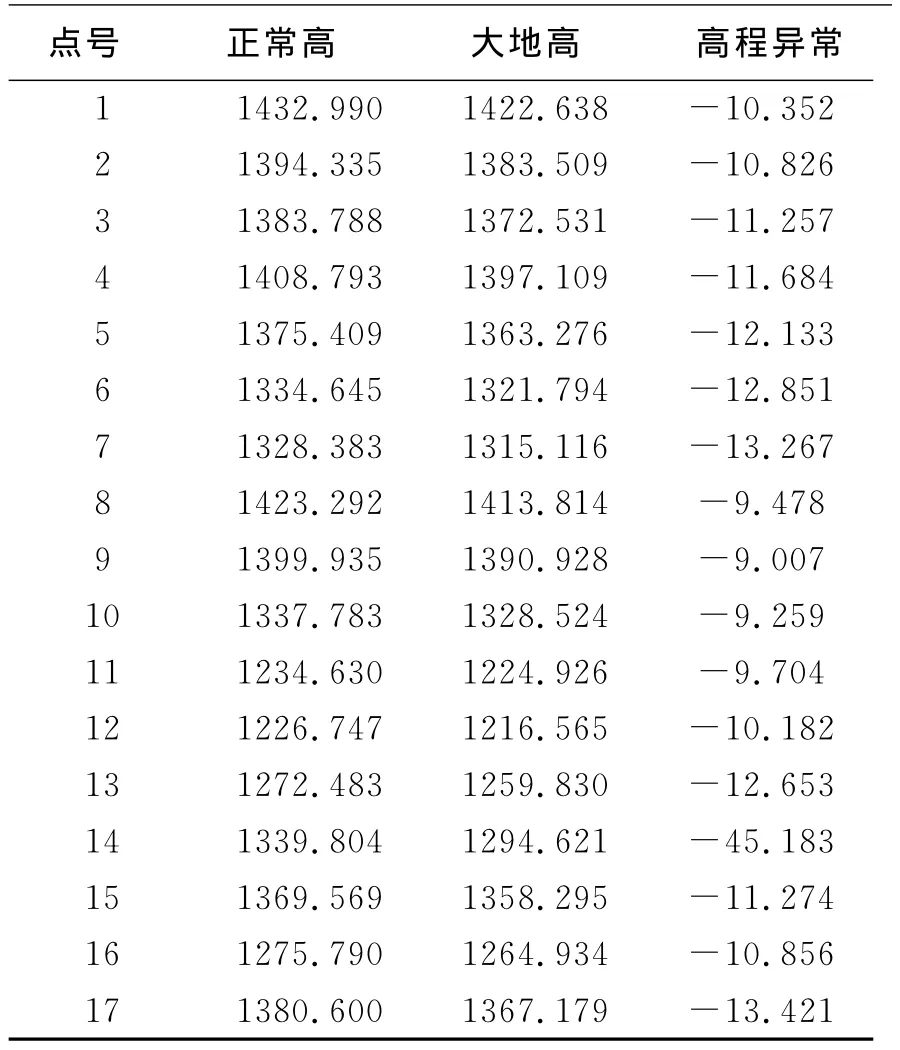
表1 某區域高程控制成果表

根據圖4，由多面函數選點原則，可將1，7，9，10，14，16，17點作為已知點，并將7，9，10，17作為擬合核函數的中心點，即已知點，建立多面函數擬合模型，對剩余的10個點進行高程擬合，用擬合所得的高程與己知的水準高程進行比較，來驗證各個多面函數擬合的精度。根據多面函數的原理和所給數據，分別求出各個待擬合點的高程異常，然后求出擬合殘差見表2所示。

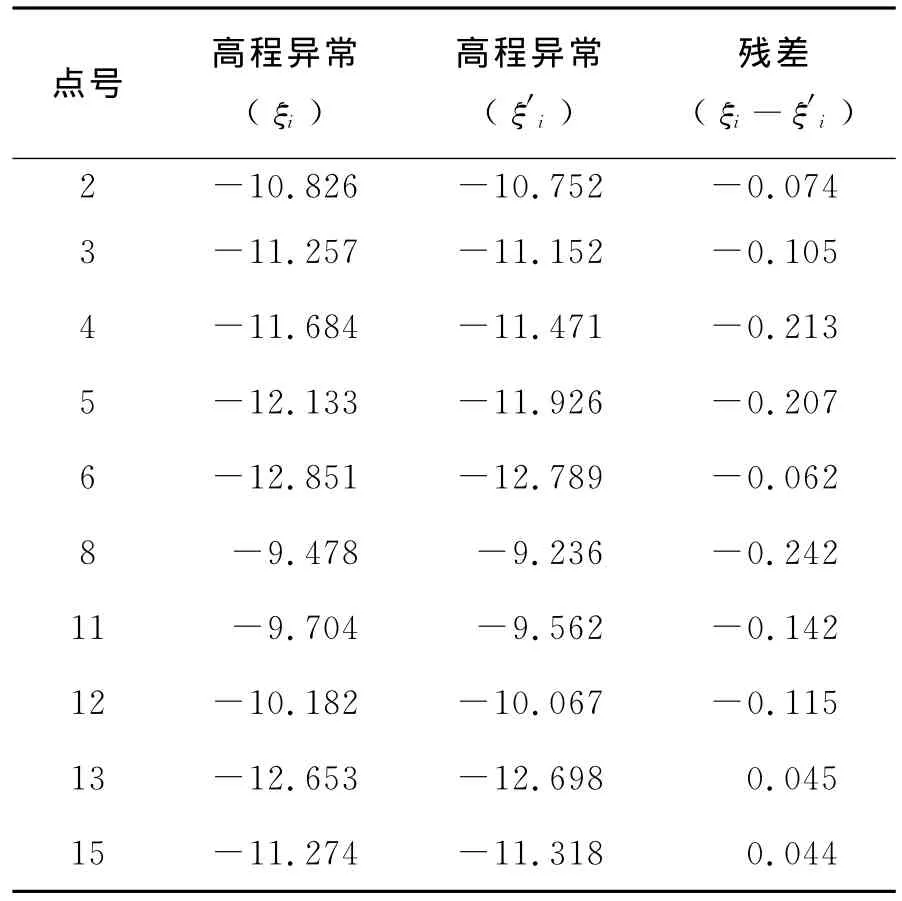
表2 多面函數法擬合點殘差／m

按照公式（5）計算出GPS水準擬合的外部符合精度[4－5]M ＝ ±0.078m.

式中n為v的個數，vi＝ξ－ξ′i.

3.2 分區擬合法

分區擬合[2－4]是把需要測量區域分成幾個小區，由于分區前一般不了解測區的高程異常變化情況，分區時可將鄰近的且高程異常值變化趨勢相近的GPS水準聯測點作為一個小區，也可以先采用比較簡單的最小二乘平面擬合法試算，將整個測區用一個平面模型來擬合，然后根據試算后的各GPS水準聯測點的高程異常值的擬合殘差大小，判定測區的高程異常起伏變化的情況。將擬合殘差大的聯測點作為高程異常的高、低變化點，分別把以這些點為中心的區域作為一個小區；同時，也要結合測區的地形變化進行劃分，還可參閱高程異常圖。分區擬合注意以下兩個問題：

1）擬合后曲面間的連接：根據測區的實際情況，每個小區內進行聯測擬合，擬合后的曲面會出現曲面相交和曲面不相交兩種情況。分區擬合后不進行平滑連接，這樣會出現同一個點有兩個不同的正常高，為避免這種情況采用數學函數進行平滑連接，以小區間有3個公共的GPS水準聯測點為佳。①對擬合后曲面相交的平滑連接這種情況：兩個小區分別采用適合自己的擬合模型擬合后，若出現相交的情形，可采用雙三次樣條函數進行連接。通過解算雙三次樣條函數，可以實現兩個小區分別擬合后的曲面相交的平滑連接，使測區的高程異常模型曲面為一光滑的物理面。若曲面間的交線是一平面曲線，為簡化計算，也可以用三次樣條函數來進行平滑。②對于擬合后曲面不相交的平滑連接：若擬合后的曲面出現不相交的情況，可采用雙三次曲面函數來進行小區間的平滑連接。實現了不相交曲面間的平滑連接，建立了測區的統一高程異常模型，測區內任意點的高程異常都可以通過擬合函數內插計算獲得。

2）分區擬合法精度評定：采用擬合法求高程異常是否能夠達到必要的精度以代替低等級的幾何水準測量，有必要對擬合結果進行精度評定。精度評定的方法主要是計算檢核點（未參與擬合的支撐點）的中誤差。

每個小區采用適合自己的數學函數進行擬合，對擬合函數的擬合精度進行評定，按公式（6）：

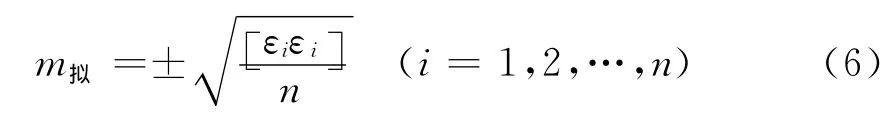
式中：εi為參加擬合的GPS水準聯測點的擬合殘差；n為參與的擬合點個數。

計算檢核點（未參與擬合的GPS水準聯測點）的擬合中誤差，按公式（7）。式中，εj為檢核點的GPS水準高程異常與擬合后計算出的高程異常之差；m為檢核點個數。

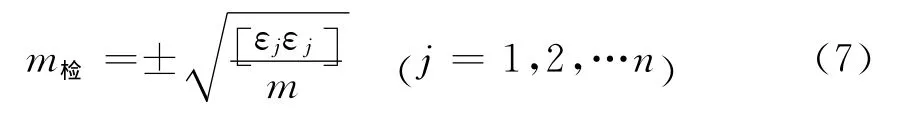
計算水準測量的限差，比較每個檢核點的εj是否超限（按照公式（8）計算），L是檢核點到最近的擬合點的距離（km）；m0為規范規定的確定限差的單位中誤差，可根據所要求的水準測量等級賦值，如該測區要求達到四等水準測量的精度要求，按規范要求，m0取20mm.

3.3 兩種方法的精度比較

為了更客觀的把兩種方法的精度高低表現出來，在研究兩種方法的高程擬合時，特地選了同樣的點作為已知點，分別用這兩種方法求出待擬合點的高程異常，這樣就更直觀的把這兩種方法擬合高程的優劣表現出來了，各種方法的精度評定結果見表3。

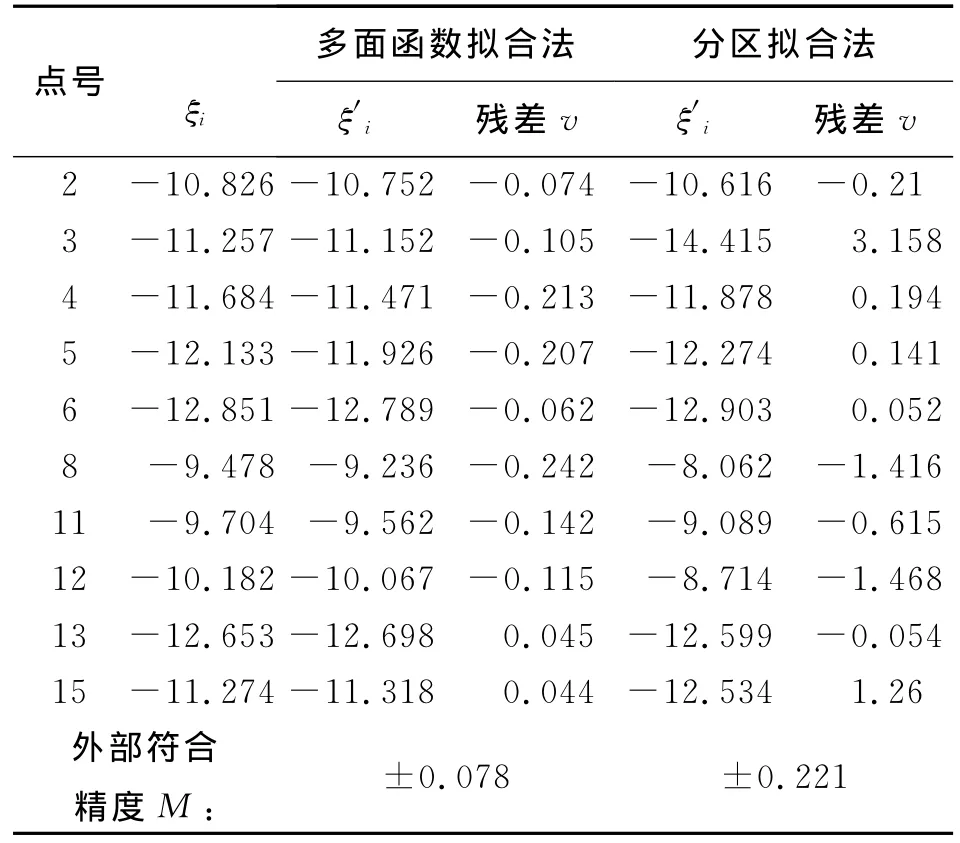
表3 不同擬合方法精度比較／m

由此表可以很清晰的看到，不管從外部符合精度還是殘差來看，多面函數擬合法在計算量和精度上優勢很明顯，結合此控制網的形狀和各點的分布，可以知道多面函數擬合法適合于地形復雜的測區擬合，當GPS水準聯測點越多、顯著點越多時，這種方法的擬合精度就越高，越能反映出測區內細部的凸凹變化程度。因此，該方法是狹長區域工程的首選擬合方法。

4 結 論

對于狹長的工程區域，跨越區域廣，高程異常變化大，除選擇幾何水準點的最佳點數和點位的最佳布設，還要注意高程的擬合方法的選擇，通過實例比較不難看出多面函數擬合法為一種合理的方法。在相同的擬合條件下，與其它方案相比，其精度可以達到最優。

[1]徐紹銓，張華海，楊志強，等.GPS測量原理與應用[M].湖北：武漢大學出版社，2008：169－174.

[2]劉長建，柴洪洲，吳洪舉，等.幾種GPS水準擬合方法的模型優選與比較[J].全球定位系統，2008，33（4）：11－14.

[3]于世全，任德平.GPS水準高程擬合的應用探討[J].煤礦現代化，2008（1）：35－36，38.

[4]李秀海，韓 冰.基于多面函數模型的GPS高程擬合精度分析[J].測繪與空間地理信息，2010，33（1）：12－13，17.