離散型多變量條件極值問題新探

●張俊杰 劉海槐 (華南師范大學數學科學學院 廣東廣州 510631)

1 問題引入

(2006年全國高中數學聯賽試題)

此題是1976年第4道IMO試題的變式，采用調整法即可求解.受文獻［1］的啟發，筆者把每個xi加強為正合數，得到了一些有趣的結論.

2 變式推廣

顯然，和為S的不同正整數分拆只有有限個，所以必有S的一個正合數分拆，使得u(n)取到最大值.

定義 若x1+x2+…+xn=S(n∈N*)，其中S∈ Z+，xi(i=1，2，…，n) 為正合數，則稱使u(n)取得最大值的數組(x1，x2，…，xn)為最優解.

下面對u(n)max進行探究.

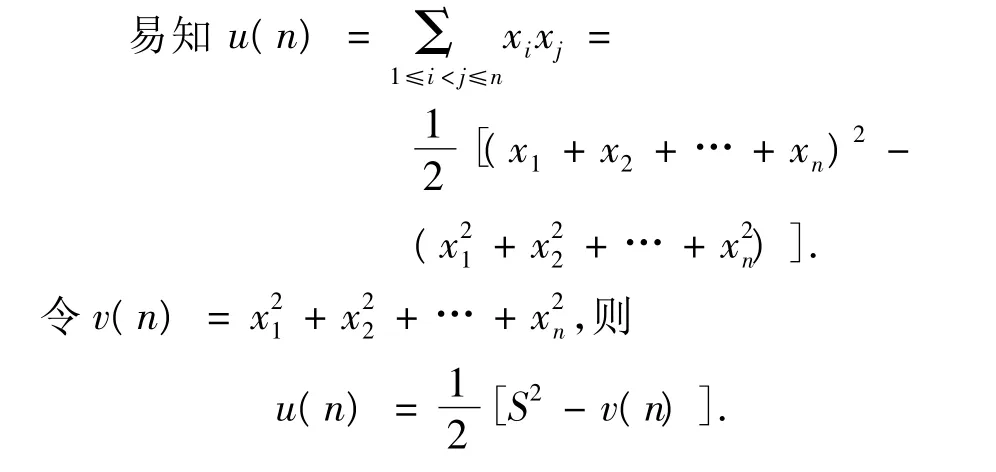
為求u(n)max的值，可先探究v(n)min.容易驗證：當S ∈ {1，2，3，5，7，11} 時，S不能表示成若干正合數之和，因此 v(n)min不存在;當 S ∈ {4，6，8，9，10，12}時，對應的n和v(n)min如表1所示.

表1 對應的n和v(n)min值

續表1

下設S≥13，u(n)取得最大值的最優解為(x1，x2，…，xn)，此時 v(n) 取得最小值，則有

性質1 xi≤9(1≤i≤ n).

證明若不然，則存在某個xj≥10(1≤j≤n).下面對xj進行分類討論：

(1) 當2|xj時，因為xj=(xj-4)+4，注意到xj-4為正合數，但

所以可用xj-4和4代替xj而使v(n)變小，這與(x1，x2，…，xn) 為最優解矛盾;

同理可得，與(x1，x2，…，xn)為最優解矛盾.

性質2 不存在xi=xj=6(1≤i＜j≤n).

證明因為xi+xj=6+6=4+4+4(1≤i ＜ j≤ n)，但

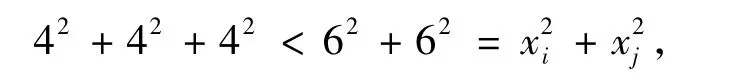
與(x1，x2，…，xn) 為最優解矛盾.

性質3 不存在xi=xj=9(1≤i＜j≤n).

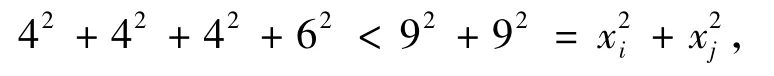
同理得出矛盾.

下面對S(S≥13)進行分類討論：

(1)4|S，即S=4k，k∈ N*且k≥4.由上述3個性質，易知當x1=x2=… =xn=4時，v(n)取得最小值

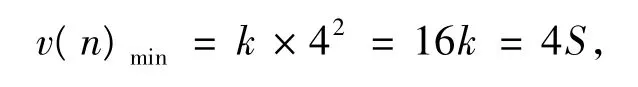
此時n=k.

(2)4|S+3，即S=4k-3，k∈N*且k≥4.因為S為奇數，由性質3知，存在唯一的某個xi=9(1≤ i≤ n)，不妨設 xn=9，則

由(1)知，當x1=x2=… =xn-1=4且xn=9時，v(n)取得最小值

(3)4|S+2，即S=4k-2，k∈N*且k≥4.因為S=4(k-2)+6為偶數，由性質2和性質3知，存在唯一的某個xi=6(1≤i≤n)，但不存在xj=9(1 ≤ j≤ n).不妨設 xn=6，則

由(1)知當x1=x2=… =xn-1=4且xn=6時，v(n)取得最小值

(4)4|S+1，即S=4k-1，k∈N*且k≥4.因為S為奇數，故存在唯一的某個xi=9(1≤i≤n)，不妨設 xn=9，則

由性質2，不妨設xn-1=6，則

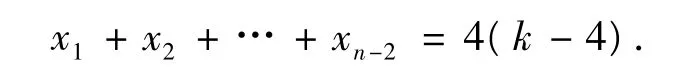
由(1)知，當x1=x2=… =xn-2=4，xn-1=6且xn=9時，v(n)取得最小值

結論當S?{1，2，3，5，7，11} 時，對應的n，v(n)min和u(n)max的值分別為表2所示(其中k∈N*).

表2 對應的n，v(n)min和u(n)max值

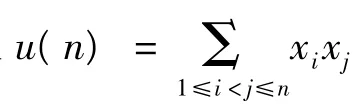
設u(n)取得最大值的最優解為(x1，x2，…，xn)，不妨設x1≤x2≤…≤xn，同理可得性質1至性質3，而且在變式2中還滿足：

性質4 x1=4.

證明若不然，則x1=6或x1=9.倘若x1=6，因為

這與(x1，x2，…，xn) 為最優解矛盾;倘若 x1=9，因為產生矛盾.故x1=4.

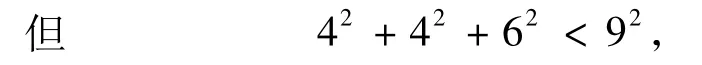
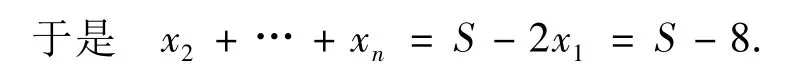
至此，變式2化歸為變式1的求解，下不贅述.

其實，還可以改變u(n)的形式和xi的條件限制，例如當xi均為正奇合數時將得到一些有趣的新結論.請讀者自行探究.

［1］ 葉軍.數學奧林匹克教程［M］.長沙：湖南師范大學出版社，2003.